Giải mục 3 trang 22, 23, 24 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 22, 23, 24 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 trang 22, 23, 24 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án, phương pháp giải và giải thích chi tiết từng bước để giúp các em hiểu rõ kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán.
Đường tiệm cận xiên
TH3
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x}}{{x + 5}}\)
Phương pháp giải:
Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 5} \right\}\)
Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x}}{{x + 5}}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{{x^2} + 5x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{3}{x}}}{{1 + \frac{5}{x}}} = 2\)
\(b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^2} - 3x}}{{x + 5}} - 2x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13x}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13}}{{1 + \frac{5}{x}}} = - 13\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [y - (2x - 3)] = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{x + 5}} - (2x - 13) = \mathop {\lim }\limits_{x \to + \infty } \frac{{65}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{65}}{x}}}{{1 + \frac{5}{x}}} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x - 13
TH4
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)
Tìm các đường tiệm cận của hàm số C(x).
Phương pháp giải:
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: \(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \); \(\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \)
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x = 0
\(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\); \(\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\)
Vậy tiệm cận ngang của đồ thị hàm số là đường thẳng y = 50
KP3
Trả lời câu hỏi Khám phá 3 trang 22 SGK Toán 12 Chân trời sáng tạo
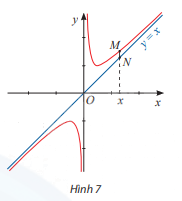
Cho đồ thị của hàm số \(y = \frac{{{x^2} + 1}}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)\) và \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)\)
b) Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x
b) MN = y – x = \(\frac{{{x^2} + 1}}{x} - x = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
- KP3
- TH3
- TH4
Trả lời câu hỏi Khám phá 3 trang 22 SGK Toán 12 Chân trời sáng tạo
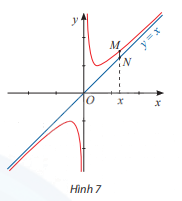
Cho đồ thị của hàm số \(y = \frac{{{x^2} + 1}}{x}\) và đường thẳng y = x. Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = x tại điểm N (Hình 7).
a) Tính \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x)\) và \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x)\)
b) Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)
Phương pháp giải:
Quan sát đồ thị
Lời giải chi tiết:
a) Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
Ta có: \(\mathop {\lim }\limits_{x \to - \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{x} = 0\); \(\mathop {\lim }\limits_{x \to + \infty } (\frac{{{x^2} + 1}}{x} - x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2} + 1 - {x^2}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{x} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = x
b) MN = y – x = \(\frac{{{x^2} + 1}}{x} - x = \frac{1}{x}\)
Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0
Trả lời câu hỏi Thực hành 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Tìm tiệm cận xiên của đồ thị hàm số \(y = \frac{{2{x^2} - 3x}}{{x + 5}}\)
Phương pháp giải:
Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 5} \right\}\)
Ta có: \(a = \mathop {\lim }\limits_{x \to + \infty } \frac{y}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{2{x^2} - 3x}}{{x + 5}}}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{{x^2} + 5x}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{2 - \frac{3}{x}}}{{1 + \frac{5}{x}}} = 2\)
\(b = \mathop {\lim }\limits_{x \to + \infty } (y - ax) = \mathop {\lim }\limits_{x \to + \infty } (\frac{{2{x^2} - 3x}}{{x + 5}} - 2x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13x}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{ - 13}}{{1 + \frac{5}{x}}} = - 13\)
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } [y - (ax + b)] = \mathop {\lim }\limits_{x \to + \infty } [y - (2x - 3)] = \mathop {\lim }\limits_{x \to + \infty } \frac{{2{x^2} - 3x}}{{x + 5}} - (2x - 13) = \mathop {\lim }\limits_{x \to + \infty } \frac{{65}}{{x + 5}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{\frac{{65}}{x}}}{{1 + \frac{5}{x}}} = 0\)
Do đó, đồ thị hàm số có tiệm cận xiên là đường thẳng y = 2x - 13
Trả lời câu hỏi Thực hành 4 trang 24 SGK Toán 12 Chân trời sáng tạo
Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \(C(x) = \frac{{50x + 2000}}{x}\)
Tìm các đường tiệm cận của hàm số C(x).
Phương pháp giải:
- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: \(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)
- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)
- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)
Lời giải chi tiết:
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 0 \right\}\)
\(\mathop {\lim }\limits_{x \to {0^ + }} C(x) = \mathop {\lim }\limits_{x \to {0^ + }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \); \(\mathop {\lim }\limits_{x \to {0^ - }} C(x) = \mathop {\lim }\limits_{x \to {0^ - }} \frac{{50x + 2000}}{x} = \frac{{2000}}{0} = + \infty \)
Vậy tiệm cận đứng của đồ thị hàm số là đường thẳng x = 0
\(\mathop {\lim }\limits_{x \to + \infty } C(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to + \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\); \(\mathop {\lim }\limits_{x \to - \infty } C(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{50x + 2000}}{x} = \mathop {\lim }\limits_{x \to - \infty } \frac{{50 + \frac{{2000}}{x}}}{1} = 50\)
Vậy tiệm cận ngang của đồ thị hàm số là đường thẳng y = 50
Giải mục 3 trang 22, 23, 24 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 1 - Chân trời sáng tạo thường xoay quanh các chủ đề về giới hạn của hàm số, đặc biệt là giới hạn tại vô cùng và giới hạn một bên. Việc nắm vững kiến thức này là nền tảng quan trọng cho việc học tập các chương trình Toán học nâng cao hơn, cũng như ứng dụng vào các lĩnh vực khoa học kỹ thuật.
Nội dung chính của Mục 3
- Khái niệm giới hạn tại vô cùng: Hiểu rõ ý nghĩa của việc hàm số tiến tới một giá trị khi x tiến tới vô cùng dương hoặc âm.
- Tính chất của giới hạn: Nắm vững các tính chất cơ bản của giới hạn, giúp đơn giản hóa việc tính toán giới hạn phức tạp.
- Giới hạn một bên: Phân biệt và tính toán giới hạn trái và giới hạn phải của hàm số tại một điểm.
- Ứng dụng của giới hạn: Sử dụng giới hạn để giải quyết các bài toán thực tế, ví dụ như tính diện tích giới hạn bởi đồ thị hàm số.
Giải chi tiết các bài tập trong Mục 3
Dưới đây là giải chi tiết các bài tập trang 22, 23, 24 SGK Toán 12 tập 1 - Chân trời sáng tạo:
Bài 1: Tính các giới hạn sau
- lim (x -> +∞) (2x + 1) / (x - 3)
- lim (x -> -∞) (x^2 + 5x + 6) / (x^2 - 2x + 1)
- lim (x -> 0+) 1/x
Giải:
- Câu a: lim (x -> +∞) (2x + 1) / (x - 3) = lim (x -> +∞) (2 + 1/x) / (1 - 3/x) = 2/1 = 2
- Câu b: lim (x -> -∞) (x^2 + 5x + 6) / (x^2 - 2x + 1) = lim (x -> -∞) (1 + 5/x + 6/x^2) / (1 - 2/x + 1/x^2) = 1/1 = 1
- Câu c: lim (x -> 0+) 1/x = +∞
Bài 2: Xét tính liên tục của hàm số f(x) = (x^2 - 1) / (x - 1) tại x = 1
Giải:
Hàm số f(x) không xác định tại x = 1. Tuy nhiên, ta có thể rút gọn f(x) = x + 1 với x ≠ 1. Do đó, lim (x -> 1) f(x) = lim (x -> 1) (x + 1) = 2. Vì f(1) không xác định, nên hàm số không liên tục tại x = 1.
Mẹo học tốt Toán 12 - Chân trời sáng tạo
- Nắm vững định nghĩa: Hiểu rõ các khái niệm cơ bản về giới hạn, tính liên tục.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các sách bài tập, đề thi thử để mở rộng kiến thức.
- Hỏi thầy cô, bạn bè: Đừng ngần ngại hỏi khi gặp khó khăn, trao đổi kiến thức với bạn bè để cùng nhau tiến bộ.
Tusach.vn hy vọng với lời giải chi tiết và những lời khuyên trên, các em sẽ học tốt môn Toán 12 - Chân trời sáng tạo. Chúc các em thành công!