Giải mục 3 trang 46,47,48 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải Mục 3 Trang 46,47,48 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo
Chào mừng các em học sinh đến với lời giải chi tiết Mục 3 trang 46, 47, 48 SGK Toán 12 tập 1 Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài tập Toán 12 và đạt kết quả cao trong các kỳ thi.
Tích của một số với một vectơ
TH7
Trả lời câu hỏi Thực hành 7 trang 47 SGK Toán 12 Chân trời sáng tạo
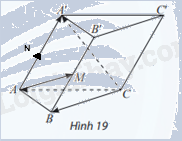
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ (Hình 19). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {CC'} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
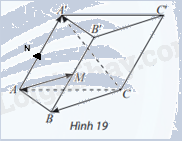
Phương pháp giải:
Áp dụng quy tắc hiệu, quy tắc hình bình hành và 2 vecto bằng nhau.
Lời giải chi tiết:
Gọi N là trung điểm AA’.
Ta có: \(\overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {CC'} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} = \overrightarrow {AB} + \overrightarrow {AN} = \overrightarrow {AM} \)
Hay \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
KP4
Trả lời câu hỏi Khám phá 4 trang 46 SGK Toán 12 Chân trời sáng tạo
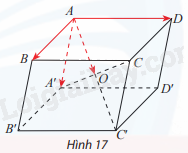
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình 17).
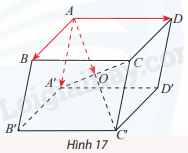
a) Tìm vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a) và vectơ \(\overrightarrow {AO} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp.
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\overrightarrow {AC'} = 2\overrightarrow {AO} \).
VD3
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Chân trời sáng tạo
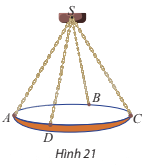
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) (Hình 21).
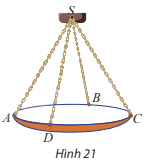
a) Sử dụng công thức \(\overrightarrow P = m\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn 10\(m/{s^2}\), tìm độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực.
b) Để chiếc đèn cân bằng thì hợp lực của 4 sợi xích phải cân bằng với trọng lực. Dựa vào tính chất của hình chóp tứ giác đều và quy tắc hình bình hành để tìm hợp lực đó rồi tìm ra lực căng của mỗi sợi xích.
Lời giải chi tiết:
a) Độ lớn trọng lực tác động lên đèn chùm là: P = mg = 5.10 = 50 (N).
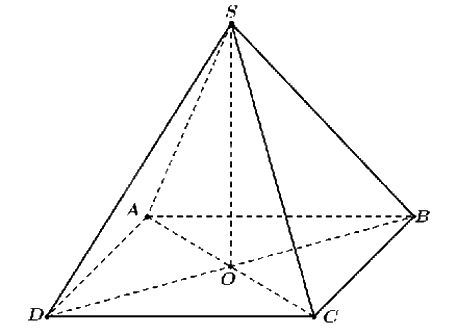
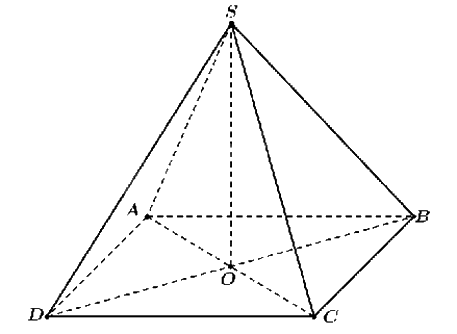
b) Giả sử đèn chùm được minh họa như hình vẽ trên.
Gọi O là tâm hình vuông ABCD.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {OS} + \overrightarrow {SA} + \overrightarrow {OS} + \overrightarrow {SB} + \overrightarrow {OS} + \overrightarrow {SC} + \overrightarrow {OS} + \overrightarrow {SD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = - 4\overrightarrow {OS} = 4\overrightarrow {SO} \)
\( \Rightarrow \left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} } \right| = \left| {4\overrightarrow {SO} } \right| = 4SO\).
Trọng lượng của vật là \(P = 50\) (N).
Suy ra \(4\left| {\overrightarrow {SO} } \right| = P = 50\). Do đó \(SO = \frac{{50}}{4} = \frac{{25}}{2}\).
Vì \(\widehat {ASC} = {60^o}\) suy ra \(\widehat {ASO} = {30^o}\).
Xét tam giác SAO vuông tại O:
\(\cos \widehat {ASO} = \frac{{SO}}{{SA}} \Leftrightarrow SA = \frac{{SO}}{{\cos \widehat {ASO}}} = \frac{{\frac{{25}}{2}}}{{\cos {{30}^o}}} = \frac{{25\sqrt 3 }}{3}\).
Vậy lực tác dụng lên mỗi sợi dây xích bằng \(\frac{{25\sqrt 3 }}{3}\) (N).
- KP4
- TH7
- VD3
Trả lời câu hỏi Khám phá 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD. A′B′C′D′ có AC′ và A′C cắt nhau tại O (Hình 17).
a) Tìm vectơ \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} \).
b) Cho biết mối quan hệ giữa vectơ tìm được ở câu a) và vectơ \(\overrightarrow {AO} \).
Phương pháp giải:
Áp dụng quy tắc hình hộp.
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \).
b) \(\overrightarrow {AC'} = 2\overrightarrow {AO} \).
Trả lời câu hỏi Thực hành 7 trang 47 SGK Toán 12 Chân trời sáng tạo
Cho hình lăng trụ ABC.A′B′C′ có M là trung điểm của BB′ (Hình 19). Đặt \(\overrightarrow {CA} = \overrightarrow a ,\overrightarrow {CB} = \overrightarrow b ,\overrightarrow {CC'} = \overrightarrow c \). Chứng minh rằng \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \)
Phương pháp giải:
Áp dụng quy tắc hiệu, quy tắc hình bình hành và 2 vecto bằng nhau.
Lời giải chi tiết:
Gọi N là trung điểm AA’.
Ta có: \(\overrightarrow {CB} - \overrightarrow {CA} + \frac{1}{2}\overrightarrow {CC'} = \overrightarrow {AB} + \frac{1}{2}\overrightarrow {AA'} = \overrightarrow {AB} + \overrightarrow {AN} = \overrightarrow {AM} \)
Hay \(\overrightarrow {AM} = \overrightarrow b - \overrightarrow a + \frac{1}{2}\overrightarrow c \).
Trả lời câu hỏi Vận dụng 3 trang 48 SGK Toán 12 Chân trời sáng tạo
Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích SA, SB, SC, SD sao cho S.ABCD là hình chóp tứ giác đều có \(\widehat {ASC} = 60^\circ \) (Hình 21).
a) Sử dụng công thức \(\overrightarrow P = m\overrightarrow g \) trong đó \(\overrightarrow g \) là vectơ gia tốc rơi tự do có độ lớn 10\(m/{s^2}\), tìm độ lớn của trọng lực \(\overrightarrow P \) tác động lên chiếc đèn chùm.
b) Tìm độ lớn của lực căng cho mỗi sợi xích.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực.
b) Để chiếc đèn cân bằng thì hợp lực của 4 sợi xích phải cân bằng với trọng lực. Dựa vào tính chất của hình chóp tứ giác đều và quy tắc hình bình hành để tìm hợp lực đó rồi tìm ra lực căng của mỗi sợi xích.
Lời giải chi tiết:
a) Độ lớn trọng lực tác động lên đèn chùm là: P = mg = 5.10 = 50 (N).
b) Giả sử đèn chùm được minh họa như hình vẽ trên.
Gọi O là tâm hình vuông ABCD.
Ta có \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {OS} + \overrightarrow {SA} + \overrightarrow {OS} + \overrightarrow {SB} + \overrightarrow {OS} + \overrightarrow {SC} + \overrightarrow {OS} + \overrightarrow {SD} = \overrightarrow 0 \)
\( \Leftrightarrow \overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} = - 4\overrightarrow {OS} = 4\overrightarrow {SO} \)
\( \Rightarrow \left| {\overrightarrow {SA} + \overrightarrow {SB} + \overrightarrow {SC} + \overrightarrow {SD} } \right| = \left| {4\overrightarrow {SO} } \right| = 4SO\).
Trọng lượng của vật là \(P = 50\) (N).
Suy ra \(4\left| {\overrightarrow {SO} } \right| = P = 50\). Do đó \(SO = \frac{{50}}{4} = \frac{{25}}{2}\).
Vì \(\widehat {ASC} = {60^o}\) suy ra \(\widehat {ASO} = {30^o}\).
Xét tam giác SAO vuông tại O:
\(\cos \widehat {ASO} = \frac{{SO}}{{SA}} \Leftrightarrow SA = \frac{{SO}}{{\cos \widehat {ASO}}} = \frac{{\frac{{25}}{2}}}{{\cos {{30}^o}}} = \frac{{25\sqrt 3 }}{3}\).
Vậy lực tác dụng lên mỗi sợi dây xích bằng \(\frac{{25\sqrt 3 }}{3}\) (N).
Giải Mục 3 Trang 46,47,48 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo: Tổng Quan và Phương Pháp Giải
Mục 3 trong SGK Toán 12 tập 1 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết cho từng bài tập trang 46, 47, 48, đồng thời phân tích phương pháp giải để các em có thể áp dụng vào các bài tập tương tự.
Nội Dung Chính của Mục 3 (Trang 46, 47, 48)
Thông thường, Mục 3 sẽ bao gồm các dạng bài tập sau:
- Bài tập vận dụng kiến thức lý thuyết: Kiểm tra khả năng hiểu và áp dụng các khái niệm đã học.
- Bài tập tính toán: Yêu cầu thực hiện các phép tính toán dựa trên công thức và định lý.
- Bài tập chứng minh: Đòi hỏi học sinh phải trình bày một cách logic và chặt chẽ để chứng minh một khẳng định nào đó.
- Bài tập thực tế: Gắn liền với các tình huống thực tế, giúp học sinh hiểu rõ hơn về ứng dụng của Toán học trong cuộc sống.
Lời Giải Chi Tiết Các Bài Tập Trang 46
Bài 1: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Bài 2: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Lời Giải Chi Tiết Các Bài Tập Trang 47
Bài 3: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Bài 4: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Lời Giải Chi Tiết Các Bài Tập Trang 48
Bài 5: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Bài 6: (Nội dung bài tập). Lời giải: ... (Giải thích chi tiết từng bước). Lưu ý: ... (Gợi ý, mẹo giải)
Phương Pháp Giải Toán 12 Hiệu Quả
- Nắm vững lý thuyết: Đọc kỹ SGK, ghi chép đầy đủ các định nghĩa, định lý và công thức.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Phân tích bài toán: Đọc kỹ đề bài, xác định rõ yêu cầu và các dữ kiện đã cho.
- Lập kế hoạch giải: Xác định phương pháp giải phù hợp và trình bày lời giải một cách logic và rõ ràng.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
Tusach.vn – Người Bạn Đồng Hành Tin Cậy
Tusach.vn cam kết cung cấp lời giải chính xác, dễ hiểu và đầy đủ cho tất cả các bài tập trong SGK Toán 12 tập 1 Chân trời sáng tạo. Chúng tôi luôn cập nhật nội dung mới nhất và lắng nghe phản hồi từ các em học sinh để cải thiện chất lượng dịch vụ.
Hãy truy cập tusach.vn thường xuyên để học Toán 12 hiệu quả và đạt kết quả cao!
| Chủ đề | Trang | Link |
|---|---|---|
| Giải Mục 3 | 46, 47, 48 | tusach.vn/giai-toan-12-muc-3-trang-46-47-48 |