Giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn hiểu sâu sắc kiến thức Toán học.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau: a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B. b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
Đề bài
Một giống cây xoan đào được trồng tại hai địa điểm A và B. Người ta thống kê đường kính thân của một số cây xoan đào 5 năm tuổi ở bảng sau:
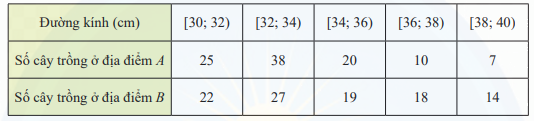 a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B. b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
a) Hãy so sánh đường kính trung bình của thân cây xoan đào trồng tại địa điểm A và địa điểm B. b) Nếu so sánh theo độ lệch chuẩn thì cây trồng tại địa điểm nào có đường kính đồng đều hơn?
Phương pháp giải - Xem chi tiết
a) Tính giá trị đại diện
Số trung bình: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\)
b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x \) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết
a)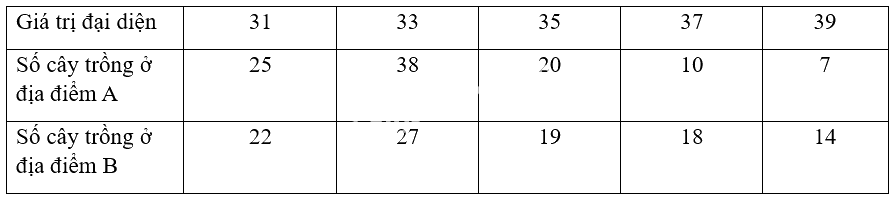
- Xét mẫu số liệu của địa điểm A:
Số trung bình: \({\overline x _A} = \frac{{25.31 + 38.33 + 20.35 + 10.37 + 7.39}}{{100}} = 33,72\)
- Xét mẫu số liệu của địa điểm B:
\({\overline x _B} = \frac{{22.31 + 27.33 + 19.35 + 18.37 + 14.39}}{{100}} = 34,5\)
Đường kính trung bình của thân cây xoan đào trồng tại địa điểm A nhỏ hơn tại địa điểm B.
b) - Xét mẫu số liệu của địa điểm A:
\({\sigma _A} = \sqrt {\frac{{{{25.31}^2} + {{38.33}^2} + {{20.35}^2} + {{10.37}^2} + {{7.39}^2}}}{{100}} - 33,{{72}^2}} = 2,32\)
- Xét mẫu số liệu của địa điểm B:
\({\sigma _B} = \sqrt {\frac{{{{22.31}^2} + {{27.33}^2} + {{19.35}^2} + {{18.37}^2} + {{14.39}^2}}}{{100}}} = 2,7\)
Vậy cây trồng tại địa điểm A có đường kính đồng đều hơn
Giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm về đạo hàm, quy tắc tính đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
Nội dung bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 4 thường có dạng như sau: Cho hàm số y = f(x). Tìm đạo hàm f'(x) và sử dụng đạo hàm để xác định các điểm cực trị, khoảng đồng biến, nghịch biến của hàm số. Hoặc, bài tập có thể yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Phương pháp giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Bước 1: Tính đạo hàm f'(x): Sử dụng các quy tắc tính đạo hàm đã học để tìm đạo hàm của hàm số f(x).
- Bước 2: Tìm điểm cực trị: Giải phương trình f'(x) = 0 để tìm các điểm nghiệm. Các điểm nghiệm này là các điểm cực trị của hàm số.
- Bước 3: Xác định khoảng đồng biến, nghịch biến: Xét dấu đạo hàm f'(x) trên các khoảng xác định của hàm số. Nếu f'(x) > 0 trên một khoảng, hàm số đồng biến trên khoảng đó. Nếu f'(x) < 0 trên một khoảng, hàm số nghịch biến trên khoảng đó.
- Bước 4: Tìm giá trị lớn nhất, giá trị nhỏ nhất: Nếu bài tập yêu cầu tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước, ta cần xét giá trị của hàm số tại các điểm cực trị và tại các đầu mút của khoảng đó.
Ví dụ minh họa giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
Ví dụ: Cho hàm số y = x3 - 3x2 + 2. Tìm đạo hàm, các điểm cực trị và khoảng đồng biến, nghịch biến của hàm số.
Giải:
- Đạo hàm: y' = 3x2 - 6x
- Điểm cực trị: Giải phương trình y' = 0, ta được 3x2 - 6x = 0 => x = 0 hoặc x = 2. Vậy hàm số có hai điểm cực trị là x = 0 và x = 2.
- Khoảng đồng biến, nghịch biến: Xét dấu y' trên các khoảng (-∞; 0), (0; 2), (2; +∞). Ta thấy:
- Trên khoảng (-∞; 0), y' > 0 => Hàm số đồng biến.
- Trên khoảng (0; 2), y' < 0 => Hàm số nghịch biến.
- Trên khoảng (2; +∞), y' > 0 => Hàm số đồng biến.
Lưu ý khi giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo
- Nắm vững các quy tắc tính đạo hàm.
- Hiểu rõ ý nghĩa của đạo hàm trong việc xác định tính đơn điệu của hàm số.
- Kiểm tra kỹ các điều kiện của bài toán để đảm bảo tính chính xác của kết quả.
- Luyện tập thường xuyên để nâng cao kỹ năng giải toán.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn tự hào là một trong những nguồn tài liệu học tập Toán 12 uy tín và được nhiều học sinh tin tưởng. Chúng tôi cung cấp đầy đủ các lời giải bài tập, đáp án trắc nghiệm, lý thuyết và các bài giảng chất lượng cao. Hãy truy cập tusach.vn để học tập hiệu quả và đạt kết quả tốt nhất!
Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài tập 4 trang 83 SGK Toán 12 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!