Giải mục 2 trang 75, 76, 77 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 75, 76, 77 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 2 trang 75, 76, 77 SGK Toán 12 tập 1 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, dễ hiểu, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng, cập nhật nhanh chóng và đầy đủ nhất để hỗ trợ quá trình học tập của các bạn.
Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm
KP
Trả lời câu hỏi Khám phá trang 75 SGK Toán 12 Chân trời sáng tạo
a) Trong biểu đồ ở Khởi động, cột thứ nhất biểu diễn số lượng học sinh có chiều cao từ 160cm đến dưới 164cm; cột thứ hai biểu diễn số lượng học sinh có chiều cao từ 164cm đến dưới 168cm, … .
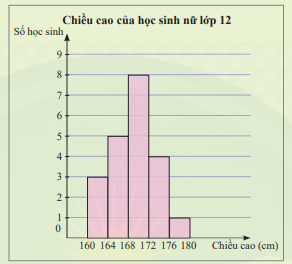
Hãy lập bảng tần số ghép nhóm cho mẫu số liệu ở , xác định giá trị đại diện của mỗi nhóm và tính số trung bình của mẫu số liệu ghép nhóm.
b) Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của nhóm tương ứng. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu mới.
Phương pháp giải:
a) Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột, các cột thường được vẽ kề nhau. Ta quy ước: cột có đầu mút trái là a và có đầu mút phải là b trên trục hoành biểu diễn cho tần số của nhóm [a; b). Giá trị đại diện của nhóm [a; b) là \(c = \frac{1}{2}(a + b)\)
b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết:
a) 
b) 
Cỡ mẫu: n = 21
Giá trị trung bình của mẫu số liệu mới: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) = \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178) = \frac{{3550}}{{21}}\)
Phương sai của mẫu số liệu mới: \({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}] = \frac{1}{{21}}[3{(162 - \frac{{3550}}{{21}})^2} + 5{(166 - \frac{{3550}}{{21}})^2} + ... + 1{(178 - \frac{{3550}}{{21}})^2}] = \frac{{8000}}{{441}}\)
Độ lệch chuẩn của mẫu số liệu mới: \(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\)
TH1
Trả lời câu hỏi Thực hành 1 trang 82 SGK Toán 12 Chân trời sáng tạo
Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm ở Khởi động

Phương pháp giải:
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết:

Cỡ mẫu: n = 21
Giá trị trung bình của mẫu số liệu mới: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) = \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178) = \frac{{3550}}{{21}}\)
Phương sai của mẫu số liệu mới: \({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}] = \frac{1}{{21}}[3{(162 - \frac{{3550}}{{21}})^2} + 5{(166 - \frac{{3550}}{{21}})^2} + ... + 1{(178 - \frac{{3550}}{{21}})^2}] = \frac{{8000}}{{441}}\)
Độ lệch chuẩn của mẫu số liệu mới: \(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\)
TH2
Trả lời câu hỏi Thực hành 2 trang 82 SGK Toán 12 Chân trời sáng tạo
Mai và Ngọc cùng sử dụng vòng đeo tay thông minh để ghi lại số bước chân hai bạn đi mỗi ngày trong một tháng. Kết quả được ghi lại ở bảng sau:
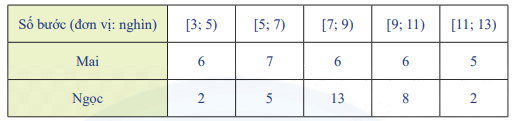
a) Hãy tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Nếu so sánh theo độ lệch chuẩn thì bạn nào có số lượng bước chân đi mỗi ngày đều đặn hơn?
Phương pháp giải:
a) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
b) Độ lệch chuẩn nhỏ hơn thì số liệu đều hơn
Lời giải chi tiết:

a) Cỡ mẫu: n = 30
- Xét mẫu số liệu của Mai:
Số trung bình: \(\overline {{x_1}} = \frac{{6.4 + 7.6 + 6.8 + 6.10 + 5.12}}{{30}} = 7,8\)
Phương sai: \({S_1}^2 = \frac{{({{6.4}^2} + {{7.6}^2} + {{6.8}^2} + {{6.10}^2} + {{5.12}^2})}}{{30}} - 7,{8^2} = 7,56\)
Độ lệch chuẩn: \({\sigma _1} = \sqrt {7,56} \approx 2,75\)
- Xét mẫu số liệu của Ngọc:
Số trung bình: \(\overline {{x_2}} = \frac{{2.4 + 5.6 + 13.8 + 8.10 + 2.12}}{{30}} = 8,2\)
Phương sai: \({S_2}^2 = \frac{{({{2.4}^2} + {{5.6}^2} + {{13.8}^2} + {{8.10}^2} + {{2.12}^2})}}{{30}} - 8,{2^2} \approx 3,83\)
Độ lệch chuẩn: \({\sigma _2} = \sqrt {3,83} \approx 1,96\)
b) Nếu so sánh theo độ lệch chuẩn thì bạn Ngọc có số lượng bước chân đi mỗi ngày đều đặn hơn
- KP
- TH1
- TH2
Trả lời câu hỏi Khám phá trang 75 SGK Toán 12 Chân trời sáng tạo
a) Trong biểu đồ ở Khởi động, cột thứ nhất biểu diễn số lượng học sinh có chiều cao từ 160cm đến dưới 164cm; cột thứ hai biểu diễn số lượng học sinh có chiều cao từ 164cm đến dưới 168cm, … .
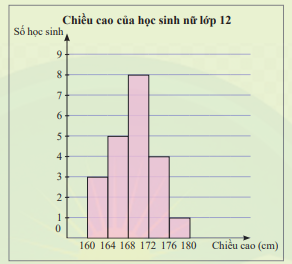
Hãy lập bảng tần số ghép nhóm cho mẫu số liệu ở , xác định giá trị đại diện của mỗi nhóm và tính số trung bình của mẫu số liệu ghép nhóm.
b) Xét mẫu số liệu mới gồm các giá trị đại diện của các nhóm, tần số của mỗi giá trị đại diện bằng tần số của nhóm tương ứng. Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu mới.
Phương pháp giải:
a) Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột, các cột thường được vẽ kề nhau. Ta quy ước: cột có đầu mút trái là a và có đầu mút phải là b trên trục hoành biểu diễn cho tần số của nhóm [a; b). Giá trị đại diện của nhóm [a; b) là \(c = \frac{1}{2}(a + b)\)
b) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết:
a) 
b) 
Cỡ mẫu: n = 21
Giá trị trung bình của mẫu số liệu mới: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) = \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178) = \frac{{3550}}{{21}}\)
Phương sai của mẫu số liệu mới: \({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}] = \frac{1}{{21}}[3{(162 - \frac{{3550}}{{21}})^2} + 5{(166 - \frac{{3550}}{{21}})^2} + ... + 1{(178 - \frac{{3550}}{{21}})^2}] = \frac{{8000}}{{441}}\)
Độ lệch chuẩn của mẫu số liệu mới: \(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\)
Trả lời câu hỏi Thực hành 1 trang 82 SGK Toán 12 Chân trời sáng tạo
Hãy tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm ở Khởi động

Phương pháp giải:
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết:

Cỡ mẫu: n = 21
Giá trị trung bình của mẫu số liệu mới: \(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}) = \frac{1}{{21}}(3.162 + 5.166 + 8.170 + 4.174 + 1.178) = \frac{{3550}}{{21}}\)
Phương sai của mẫu số liệu mới: \({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}] = \frac{1}{{21}}[3{(162 - \frac{{3550}}{{21}})^2} + 5{(166 - \frac{{3550}}{{21}})^2} + ... + 1{(178 - \frac{{3550}}{{21}})^2}] = \frac{{8000}}{{441}}\)
Độ lệch chuẩn của mẫu số liệu mới: \(\sigma = \sqrt {{S^2}} = \sqrt {\frac{{8000}}{{441}}} = \frac{{40\sqrt 5 }}{{21}}\)
Trả lời câu hỏi Thực hành 2 trang 82 SGK Toán 12 Chân trời sáng tạo
Mai và Ngọc cùng sử dụng vòng đeo tay thông minh để ghi lại số bước chân hai bạn đi mỗi ngày trong một tháng. Kết quả được ghi lại ở bảng sau:
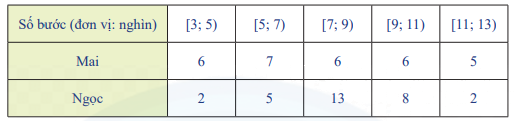
a) Hãy tính số trung bình và độ lệch chuẩn của mẫu số liệu ghép nhóm trên.
b) Nếu so sánh theo độ lệch chuẩn thì bạn nào có số lượng bước chân đi mỗi ngày đều đặn hơn?
Phương pháp giải:
a) Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
b) Độ lệch chuẩn nhỏ hơn thì số liệu đều hơn
Lời giải chi tiết:

a) Cỡ mẫu: n = 30
- Xét mẫu số liệu của Mai:
Số trung bình: \(\overline {{x_1}} = \frac{{6.4 + 7.6 + 6.8 + 6.10 + 5.12}}{{30}} = 7,8\)
Phương sai: \({S_1}^2 = \frac{{({{6.4}^2} + {{7.6}^2} + {{6.8}^2} + {{6.10}^2} + {{5.12}^2})}}{{30}} - 7,{8^2} = 7,56\)
Độ lệch chuẩn: \({\sigma _1} = \sqrt {7,56} \approx 2,75\)
- Xét mẫu số liệu của Ngọc:
Số trung bình: \(\overline {{x_2}} = \frac{{2.4 + 5.6 + 13.8 + 8.10 + 2.12}}{{30}} = 8,2\)
Phương sai: \({S_2}^2 = \frac{{({{2.4}^2} + {{5.6}^2} + {{13.8}^2} + {{8.10}^2} + {{2.12}^2})}}{{30}} - 8,{2^2} \approx 3,83\)
Độ lệch chuẩn: \({\sigma _2} = \sqrt {3,83} \approx 1,96\)
b) Nếu so sánh theo độ lệch chuẩn thì bạn Ngọc có số lượng bước chân đi mỗi ngày đều đặn hơn
Giải mục 2 trang 75, 76, 77 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Chân trời sáng tạo tập trung vào các kiến thức về giới hạn của hàm số. Đây là một trong những chủ đề quan trọng, nền tảng cho việc học tập các kiến thức nâng cao hơn trong chương trình Toán 12. Việc nắm vững các khái niệm, định lý và kỹ năng giải bài tập liên quan đến giới hạn là vô cùng cần thiết để đạt kết quả tốt trong các kỳ thi.
Nội dung chính của Mục 2
- Khái niệm giới hạn của hàm số tại một điểm: Hiểu rõ ý nghĩa của giới hạn, cách xác định giới hạn của hàm số khi x tiến tới một giá trị cụ thể.
- Các tính chất của giới hạn: Nắm vững các tính chất của giới hạn như tính chất cộng, trừ, nhân, chia, giới hạn của tích, thương, lũy thừa.
- Các dạng giới hạn cơ bản: Giải quyết các bài toán giới hạn bằng cách sử dụng các công thức và kỹ thuật biến đổi đại số.
- Giới hạn vô cùng: Tìm hiểu về giới hạn của hàm số khi x tiến tới vô cùng dương hoặc vô cùng âm.
Giải chi tiết bài tập trang 75, 76, 77
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 75, 76, 77 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 75)
Đề bài: Tính các giới hạn sau: a) lim (x→2) (x^2 + 3x - 1); b) lim (x→-1) (2x^3 - 5x + 2)
Lời giải:
- a) lim (x→2) (x^2 + 3x - 1) = 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9
- b) lim (x→-1) (2x^3 - 5x + 2) = 2*(-1)^3 - 5*(-1) + 2 = -2 + 5 + 2 = 5
Bài 2: (Trang 76)
Đề bài: Tính các giới hạn sau: a) lim (x→3) (x - 3) / (x^2 - 9); b) lim (x→1) (x^2 - 1) / (x - 1)
Lời giải:
- a) lim (x→3) (x - 3) / (x^2 - 9) = lim (x→3) (x - 3) / ((x - 3)(x + 3)) = lim (x→3) 1 / (x + 3) = 1 / (3 + 3) = 1/6
- b) lim (x→1) (x^2 - 1) / (x - 1) = lim (x→1) (x - 1)(x + 1) / (x - 1) = lim (x→1) (x + 1) = 1 + 1 = 2
Bài 3: (Trang 77)
Đề bài: Tính giới hạn: lim (x→0) sin(x) / x
Lời giải:
Đây là một giới hạn lượng giác cơ bản. Sử dụng định lý giới hạn đặc biệt, ta có: lim (x→0) sin(x) / x = 1
Mẹo giải bài tập về giới hạn
- Phân tích và đơn giản hóa biểu thức: Trước khi tính giới hạn, hãy cố gắng phân tích và đơn giản hóa biểu thức để loại bỏ các yếu tố gây khó khăn.
- Sử dụng các công thức giới hạn đặc biệt: Nắm vững các công thức giới hạn đặc biệt như lim (x→0) sin(x) / x = 1, lim (x→0) (1 - cos(x)) / x = 0.
- Áp dụng các tính chất của giới hạn: Sử dụng các tính chất của giới hạn để biến đổi biểu thức và tính giới hạn một cách dễ dàng hơn.
- Kiểm tra lại kết quả: Sau khi tính giới hạn, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Hy vọng với lời giải chi tiết và các hướng dẫn trên, các bạn học sinh sẽ hiểu rõ hơn về Mục 2 SGK Toán 12 tập 1 Chân trời sáng tạo và tự tin giải các bài tập liên quan đến giới hạn. Chúc các bạn học tập tốt!