Trả lời câu hỏi Hoạt động 2 trang 33, 34 SGK Toán 12 Chân trời sáng tạo
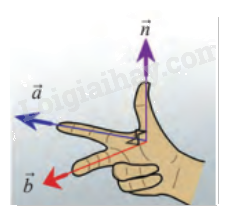
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) có cặp vectơ chỉ phương \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\), \(\vec b = \left( {{b_1};{b_2};{b_3}} \right)\). Xét vectơ \(\vec n = \left( {{a_2}{b_3} - {a_3}{b_2};{a_3}{b_1} - {a_1}{b_3};{a_1}{b_2} - {a_2}{b_1}} \right)\).
a) Vectơ \(\vec n\) có khác \(\vec 0\) hay không?
b) Tính \(\vec a.\vec n\); \(\vec b.\vec n\).
c) Vectơ \(\vec n\) có phải là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\) không?
Phương pháp giải:
a) Giả sử \(\vec n = \vec 0\), sau đó chứng minh rằng \(\vec a\) và \(\vec b\) là hai vectơ cùng phương. Điều này là vô lí do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\).
b) Sử dụng công thức tích vô hướng của hai vectơ trong không gian.
c) Để chứng minh \(\vec n\) là vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\), ta chỉ ra rằng \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\).
Lời giải chi tiết:
a) Giả sử \(\vec n = \vec 0\), khi đó \({a_2}{b_3} - {a_3}{b_2} = {a_3}{b_1} - {a_1}{b_3} = {a_1}{b_2} - {a_2}{b_1} = 0\).
Với trường hợp \({b_1}\), \({b_2}\), \({b_3}\) cùng khác 0, ta suy ra \(\frac{{{a_1}}}{{{b_1}}} = \frac{{{a_2}}}{{{b_2}}} = \frac{{{a_3}}}{{{b_3}}}\), điều này có nghĩa \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Nếu \({b_1} = 0\) thì \({a_1} = 0\), ta vẫn thu được kết quả \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Các trường hợp còn lại cho ra kết quả tương tự.
Như vậy \(\vec a\) và \(\vec b\) là hai vectơ cùng phương.
Mặt khác, do \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec a\) và \(\vec b\) là hai vectơ không cùng phương, mâu thuẫn.
Như vậy \(\vec n \ne \vec 0\).
b) Ta có:
+)\(\vec a.\vec n = {a_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {a_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {a_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {a_1}{a_2}{b_3} - {a_1}{a_3}{b_2} + {a_2}{a_3}{b_1} - {a_2}{a_1}{b_3} + {a_3}{a_1}{b_2} - {a_3}{a_2}{b_1} = 0\)
+) \(\vec b.\vec n = {b_1}\left( {{a_2}{b_3} - {a_3}{b_2}} \right) + {b_2}\left( {{a_3}{b_1} - {a_1}{b_3}} \right) + {b_3}\left( {{a_1}{b_2} - {a_2}{b_1}} \right)\)
\( = {b_1}{a_2}{b_3} - {b_1}{a_3}{b_2} + {b_2}{a_3}{b_1} - {b_2}{a_1}{b_3} + {b_3}{a_1}{b_2} - {b_3}{a_2}{b_1} = 0\)
Như vậy \(\vec a.\vec n = \vec b.\vec n = 0\).
c) Theo câu b, ta có \(\vec a.\vec n = \vec b.\vec n = 0\), điều này có nghĩa là \(\vec n\) có giá vuông góc với giá của \(\vec a\) và \(\vec b\). Mà \(\vec a\) và \(\vec b\) là một cặp vectơ chỉ phương của \(\left( \alpha \right)\), nên \(\vec n\) có giá vuông góc với mặt phẳng \(\left( \alpha \right)\). Như vậy \(\vec n\) là một vectơ pháp tuyến của \(\left( \alpha \right)\).