Giải mục 3 trang 35, 36, 37, 38 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 35, 36, 37, 38 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3, trang 35, 36, 37, 38 sách giáo khoa Toán 12 tập 2 chương trình Chân trời sáng tạo.
Chúng tôi giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong học tập.
Trong không gian (Oxyz), cho mặt phẳng (left( alpha right)) đi qua điểm ({M_0}left( {1;2;3} right)) và nhận (vec n = left( {7;5;2} right)) làm vectơ pháp tuyến. Gọi (Mleft( {x;y;z} right)) là một điểm tuỳ ý trong không gian. Tính tích vô hướng (vec n.overrightarrow {{M_0}M} ) theo (x,y,z).
TH3
Trả lời câu hỏi Thực hành 3 trang 36 SGK Toán 12 Chân trời sáng tạo
Cho hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có phương trình tổng quát là \(\left( \alpha \right):2x + 2y - 3z - 4 = 0\) và \(\left( \beta \right):x + 4z - 12 = 0\).
a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\).
b) Tìm điểm thuộc mặt phẳng \(\left( \alpha \right)\) trong số các điểm \(M\left( {1;0;1} \right)\), \(N\left( {1;1;0} \right)\).
Phương pháp giải:
a) Một vectơ pháp tuyến của mặt phẳng có phương trình \(Ax + By + Cz + D = 0\) (trong đó \(A\), \(B\), \(C\) không đồng thời bằng 0) là \(\vec n = \left( {A,B,C} \right)\).
b) Điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) nằm trên mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\) khi và chỉ khi \(A{x_0} + B{y_0} + C{z_0} + D = 0\)
Lời giải chi tiết:
a) Phương trình mặt phẳng \(\left( \alpha \right)\) là \(2x + 2y - 3z - 4 = 0\) nên \(\left( \alpha \right)\) nhận \(\overrightarrow {{n_{\left( \alpha \right)}}} = \left( {2;2; - 3} \right)\) làm một vectơ pháp tuyến.
Phương trình mặt phẳng \(\left( \beta \right)\) là \(x + 4z - 12 = 0\) nên \(\left( \beta \right)\) nhận \(\overrightarrow {{n_{\left( \beta \right)}}} = \left( {1;0;4} \right)\) làm một vectơ pháp tuyến.
b) Thay điểm \(M\left( {1;0;1} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.0 - 3.1 - 4 = - 5 \ne 0\).
Vậy điểm \(M\) không thuộc \(\left( \alpha \right)\).
Thay điểm \(N\left( {1;1;0} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.1 - 3.0 - 4 = 0\).
Vậy điểm \(N\) thuộc \(\left( \alpha \right)\).
HĐ4
Trả lời câu hỏi Hoạt động 4 trang 36 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A,B,C} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x,y,z} \right)\) là một điểm tuỳ ý trong không gian.
a) Tìm toạ độ của \(\overrightarrow {{M_0}M} \).
b) Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).
c) Lập phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right)\)
b) Sử dụng công thức tích vô hướng để tính \(\vec n.\overrightarrow {{M_0}M} \).
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\)
Lời giải chi tiết:
a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right) = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
b) Ta có: \(\vec n.\overrightarrow {{M_0}M} = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right)\)
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\).
Suy ra \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
HĐ5
Trả lời câu hỏi Hoạt động 5 trang 36 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {0,2,1} \right)\) và có cặp vectơ chỉ phương là \(\vec a = \left( {1;3;1} \right)\), \(\vec b = \left( {2;0;1} \right)\)
a) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Do \(\left( \alpha \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.
b) Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là .
Lời giải chi tiết:
a) Do \(\left( \alpha \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là:
\(\left[ {\vec a,\vec b} \right] = \left( {3.1 - 1.0;1.2 - 1.1;1.0 - 3.2} \right) = \left( {3;1; - 6} \right)\).
Vậy \(\left( \alpha \right)\) nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến.
b) Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\left( {0,2,1} \right)\) và nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến, nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\(3\left( {x - 0} \right) + 1\left( {y - 2} \right) - 6\left( {z - 1} \right) = 0 \Leftrightarrow 3x + y - 6z + 4 = 0\).
HĐ6
Trả lời câu hỏi Hoạt động 6 trang 37 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\).
a) Tìm toạ độ một cặp vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\).
b) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
c) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\), \(B\), \(C\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
c) Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;2} \right)\) và \(\overrightarrow {AC} = \left( {5;2;0} \right)\).
b) Do \(\left( \alpha \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;2} \right)\) và \(\overrightarrow {AC} = \left( {5;2;0} \right)\), nên một vectơ pháp tuyến của \(\left( \alpha \right)\) là:
\(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {3.0 - 2.2;2.5 - 2.0;2.2 - 3.5} \right) = \left( { - 4;10; - 11} \right)\).
c) Mặt phẳng \(\left( \alpha \right)\) đi qua \(A\left( {0;1;1} \right)\) và có một vectơ pháp tuyến là \(\vec n = \left( { - 4;10; - 11} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\( - 4\left( {x - 0} \right) + 10\left( {y - 1} \right) - 11\left( {z - 1} \right) = 0 \Leftrightarrow - 4x + 10y - 11z + 1 = 0\).
TH4
Trả lời câu hỏi Thực hành 4 trang 38 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\).
b) \(\left( P \right)\) đi qua điểm \(B\left( { - 2;3;0} \right)\) và có cặp vectơ chỉ phương là \(\vec u = \left( {2;2; - 1} \right)\), \(\vec v = \left( {3;1;0} \right)\).
c) \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\).
d) \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\).
Phương pháp giải:
a) Phương trình mặt phẳng \(\left( P \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
b) Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\vec u,\vec v} \right]\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.
c) Xác định một cặp vectơ chỉ phương, từ đó tính tích có hướng của cặp vectơ chỉ phương đó để tìm một vectơ pháp tuyến của \(\left( P \right)\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.
d) Sử dụng phương trình mặt phẳng theo đoạn chắn.
Lời giải chi tiết:
a) Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\) nên có phương trình là \(5\left( {x - 2} \right) - 2\left( {y - 0} \right) + 7\left( {z + 1} \right) = 0 \Leftrightarrow 5x - 2y + 7z - 3 = 0\).
b) Một vectơ pháp tuyến của \(\left( P \right)\) là:
\(\vec n = \left[ {\vec u,\vec v} \right] = \left( {2.0 - \left( { - 1} \right).1; - 1.3 - 2.0;2.1 - 2.3} \right) = \left( {1; - 3; - 4} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua \(B\left( { - 2;3;0} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1; - 3; - 4} \right)\) nên có phương trình là \(1\left( {x + 2} \right) - 3\left( {y - 3} \right) - 4\left( {z - 0} \right) = 0 \Leftrightarrow x - 3y - 4z + 11 = 0\).
c) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\) nên có 1 cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {1;1;2} \right)\) và \(\overrightarrow {AC} = \left( {2;0;1} \right)\). Do đó một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1.1 - 2.0;2.2 - 1.1;1.0 - 1.2} \right) = \left( {1;3; - 2} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua \(A\left( {2;1;5} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1;3; - 2} \right)\) nên có phương trình là \(1\left( {x - 2} \right) + 3\left( {y - 1} \right) - 2\left( {z - 5} \right) = 0 \Leftrightarrow x + 3y - 2z + 5 = 0\).
d) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\) nên phương trình mặt phẳng \(\left( P \right)\) là \(\frac{x}{7} + \frac{y}{{ - 2}} + \frac{z}{9} = 1\).
VD3
Trả lời câu hỏi Vận dụng 3 trang 38 SGK Toán 12 Chân trời sáng tạo
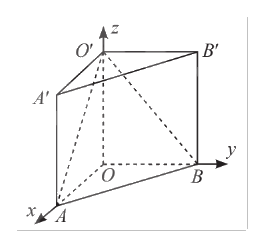
Trong không gian \(Oxyz\), cho hình lăng trụ \(OAB.O'A'B'\). Biết \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\). Viết phương trình các mặt phẳng \(\left( {O'AB} \right)\) và \(\left( {O'A'B'} \right)\).
Phương pháp giải:
Viết phương trình mặt phẳng \(\left( {O'AB} \right)\) dưới dạng phương trình mặt phẳng theo đoạn chắn. Viết phương trình mặt phẳng \(\left( {O'A'B'} \right)\) do nó đi qua điểm \(O'\) và có một vectơ pháp tuyến \(OO'\).
Lời giải chi tiết:
Mặt phẳng \(\left( {O'AB} \right)\) đi qua \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'AB} \right)\) là \(\frac{x}{2} + \frac{y}{3} + \frac{z}{5} = 1\).
Theo hình vẽ, hình lăng trụ \(OAB.O'A'B'\) có các cạnh bên vuông góc với đáy, nên ta có \(OO' \bot \left( {O'A'B'} \right)\). Suy ra \[\overrightarrow {OO'} = \left( {0;0;5} \right)\] là một vectơ pháp tuyến của mặt phẳng \(\left( {O'A'B'} \right)\).
Hơn nữa, mặt phẳng \(\left( {O'A'B'} \right)\) đi qua \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'A'B'} \right)\) là \(0\left( {x - 0} \right) + 0\left( {y - 0} \right) + 5\left( {z - 5} \right) = 0 \Leftrightarrow z - 5 = 0\).
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 35 SGK Toán 12 Chân trời sáng tạo
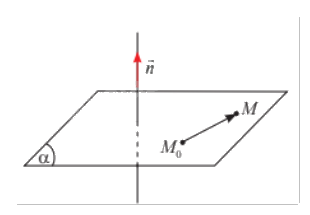
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {1;2;3} \right)\) và nhận \(\vec n = \left( {7;5;2} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x;y;z} \right)\) là một điểm tuỳ ý trong không gian. Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \) theo \(x,y,z\).
Phương pháp giải:
Tính toạ độ vectơ \(\overrightarrow {{M_0}M} \), sau đó tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).
Lời giải chi tiết:
Toạ độ của vectơ \(\overrightarrow {{M_0}M} \) là \(\left( {x - 1;y - 2;z - 3} \right)\)
Suy ra \(\vec n.\overrightarrow {{M_0}M} = 7\left( {x - 1} \right) + 5\left( {y - 2} \right) + 2\left( {z - 3} \right) = 7x + 5y + 2z - 23\)
- HĐ3
- TH3
- HĐ4
- HĐ5
- HĐ6
- TH4
- VD3
Trả lời câu hỏi Hoạt động 3 trang 35 SGK Toán 12 Chân trời sáng tạo
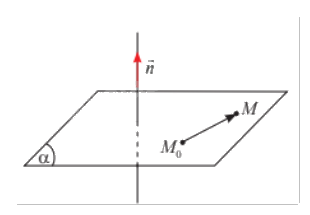
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {1;2;3} \right)\) và nhận \(\vec n = \left( {7;5;2} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x;y;z} \right)\) là một điểm tuỳ ý trong không gian. Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \) theo \(x,y,z\).
Phương pháp giải:
Tính toạ độ vectơ \(\overrightarrow {{M_0}M} \), sau đó tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).
Lời giải chi tiết:
Toạ độ của vectơ \(\overrightarrow {{M_0}M} \) là \(\left( {x - 1;y - 2;z - 3} \right)\)
Suy ra \(\vec n.\overrightarrow {{M_0}M} = 7\left( {x - 1} \right) + 5\left( {y - 2} \right) + 2\left( {z - 3} \right) = 7x + 5y + 2z - 23\)
Trả lời câu hỏi Thực hành 3 trang 36 SGK Toán 12 Chân trời sáng tạo
Cho hai mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\) có phương trình tổng quát là \(\left( \alpha \right):2x + 2y - 3z - 4 = 0\) và \(\left( \beta \right):x + 4z - 12 = 0\).
a) Tìm một vectơ pháp tuyến của mỗi mặt phẳng \(\left( \alpha \right)\), \(\left( \beta \right)\).
b) Tìm điểm thuộc mặt phẳng \(\left( \alpha \right)\) trong số các điểm \(M\left( {1;0;1} \right)\), \(N\left( {1;1;0} \right)\).
Phương pháp giải:
a) Một vectơ pháp tuyến của mặt phẳng có phương trình \(Ax + By + Cz + D = 0\) (trong đó \(A\), \(B\), \(C\) không đồng thời bằng 0) là \(\vec n = \left( {A,B,C} \right)\).
b) Điểm \(M\left( {{x_0};{y_0};{z_0}} \right)\) nằm trên mặt phẳng \(\left( \alpha \right):Ax + By + Cz + D = 0\) khi và chỉ khi \(A{x_0} + B{y_0} + C{z_0} + D = 0\)
Lời giải chi tiết:
a) Phương trình mặt phẳng \(\left( \alpha \right)\) là \(2x + 2y - 3z - 4 = 0\) nên \(\left( \alpha \right)\) nhận \(\overrightarrow {{n_{\left( \alpha \right)}}} = \left( {2;2; - 3} \right)\) làm một vectơ pháp tuyến.
Phương trình mặt phẳng \(\left( \beta \right)\) là \(x + 4z - 12 = 0\) nên \(\left( \beta \right)\) nhận \(\overrightarrow {{n_{\left( \beta \right)}}} = \left( {1;0;4} \right)\) làm một vectơ pháp tuyến.
b) Thay điểm \(M\left( {1;0;1} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.0 - 3.1 - 4 = - 5 \ne 0\).
Vậy điểm \(M\) không thuộc \(\left( \alpha \right)\).
Thay điểm \(N\left( {1;1;0} \right)\) vào phương trình mặt phẳng \(\left( \alpha \right)\), ta được:
\(2.1 + 2.1 - 3.0 - 4 = 0\).
Vậy điểm \(N\) thuộc \(\left( \alpha \right)\).
Trả lời câu hỏi Hoạt động 4 trang 36 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A,B,C} \right)\) làm vectơ pháp tuyến. Gọi \(M\left( {x,y,z} \right)\) là một điểm tuỳ ý trong không gian.
a) Tìm toạ độ của \(\overrightarrow {{M_0}M} \).
b) Tính tích vô hướng \(\vec n.\overrightarrow {{M_0}M} \).
c) Lập phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right)\)
b) Sử dụng công thức tích vô hướng để tính \(\vec n.\overrightarrow {{M_0}M} \).
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\)
Lời giải chi tiết:
a) Toạ độ của \(\overrightarrow {{M_0}M} \) là \(\left( {{x_M} - {x_{{M_0}}};{y_M} - {y_{{M_0}}};{z_M} - {z_{{M_0}}}} \right) = \left( {x - {x_0};y - {y_0};z - {z_0}} \right)\)
b) Ta có: \(\vec n.\overrightarrow {{M_0}M} = A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right)\)
c) Để lập được phương trình tổng quát của mặt phẳng \(\left( \alpha \right)\), điểm \(M\left( {x,y,z} \right)\) được chọn phải nằm trên \(\left( \alpha \right)\), điều này có nghĩa là \(\vec n.\overrightarrow {{M_0}M} = 0\).
Suy ra \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
Vậy phương trình mặt phẳng \(\left( \alpha \right)\) là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\)
Trả lời câu hỏi Hoạt động 5 trang 36 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua điểm \(M\left( {0,2,1} \right)\) và có cặp vectơ chỉ phương là \(\vec a = \left( {1;3;1} \right)\), \(\vec b = \left( {2;0;1} \right)\)
a) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
b) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Do \(\left( \alpha \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.
b) Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là .
Lời giải chi tiết:
a) Do \(\left( \alpha \right)\) nhận \(\vec a\) và \(\vec b\) làm một cặp vectơ chỉ phương, nên \(\left( \alpha \right)\) sẽ nhận vectơ \(\vec n = \left[ {\vec a,\vec b} \right]\) làm một vectơ pháp tuyến.
Tích có hướng của hai vectơ \(\vec a\) và \(\vec b\) là:
\(\left[ {\vec a,\vec b} \right] = \left( {3.1 - 1.0;1.2 - 1.1;1.0 - 3.2} \right) = \left( {3;1; - 6} \right)\).
Vậy \(\left( \alpha \right)\) nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến.
b) Mặt phẳng \(\left( \alpha \right)\) đi qua \(M\left( {0,2,1} \right)\) và nhận \(\vec n = \left( {3;1; - 6} \right)\) làm một vectơ pháp tuyến, nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\(3\left( {x - 0} \right) + 1\left( {y - 2} \right) - 6\left( {z - 1} \right) = 0 \Leftrightarrow 3x + y - 6z + 4 = 0\).
Trả lời câu hỏi Hoạt động 6 trang 37 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\).
a) Tìm toạ độ một cặp vectơ chỉ phương của mặt phẳng \(\left( \alpha \right)\).
b) Tìm toạ độ một vectơ pháp tuyến của mặt phẳng \(\left( \alpha \right)\).
c) Lập phương trình của mặt phẳng \(\left( \alpha \right)\).
Phương pháp giải:
a) Mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\), \(B\), \(C\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \).
b) Một vectơ pháp tuyến của \(\left( \alpha \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right]\).
c) Phương trình mặt phẳng \(\left( \alpha \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
Lời giải chi tiết:
a) Mặt phẳng \(\left( \alpha \right)\) đi qua ba điểm \(A\left( {0;1;1} \right)\), \(B\left( {2;4;3} \right)\), \(C\left( {5;3;1} \right)\) nên có cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;2} \right)\) và \(\overrightarrow {AC} = \left( {5;2;0} \right)\).
b) Do \(\left( \alpha \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {2;3;2} \right)\) và \(\overrightarrow {AC} = \left( {5;2;0} \right)\), nên một vectơ pháp tuyến của \(\left( \alpha \right)\) là:
\(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {3.0 - 2.2;2.5 - 2.0;2.2 - 3.5} \right) = \left( { - 4;10; - 11} \right)\).
c) Mặt phẳng \(\left( \alpha \right)\) đi qua \(A\left( {0;1;1} \right)\) và có một vectơ pháp tuyến là \(\vec n = \left( { - 4;10; - 11} \right)\) nên phương trình mặt phẳng \(\left( \alpha \right)\) là:
\( - 4\left( {x - 0} \right) + 10\left( {y - 1} \right) - 11\left( {z - 1} \right) = 0 \Leftrightarrow - 4x + 10y - 11z + 1 = 0\).
Trả lời câu hỏi Thực hành 4 trang 38 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\).
b) \(\left( P \right)\) đi qua điểm \(B\left( { - 2;3;0} \right)\) và có cặp vectơ chỉ phương là \(\vec u = \left( {2;2; - 1} \right)\), \(\vec v = \left( {3;1;0} \right)\).
c) \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\).
d) \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\).
Phương pháp giải:
a) Phương trình mặt phẳng \(\left( P \right)\) đi qua \({M_0}\left( {{x_0},{y_0},{z_0}} \right)\) và nhận \(\vec n = \left( {A;B;C} \right)\) làm một vectơ pháp tuyến là \(A\left( {x - {x_0}} \right) + B\left( {y - {y_0}} \right) + C\left( {z - {z_0}} \right) = 0\).
b) Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\vec u,\vec v} \right]\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.
c) Xác định một cặp vectơ chỉ phương, từ đó tính tích có hướng của cặp vectơ chỉ phương đó để tìm một vectơ pháp tuyến của \(\left( P \right)\). Sau đó viết phương trình mặt phẳng \(\left( P \right)\) khi biết một điểm đi qua và một vectơ pháp tuyến.
d) Sử dụng phương trình mặt phẳng theo đoạn chắn.
Lời giải chi tiết:
a) Mặt phẳng \(\left( P \right)\) đi qua điểm \(A\left( {2;0; - 1} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {5; - 2;7} \right)\) nên có phương trình là \(5\left( {x - 2} \right) - 2\left( {y - 0} \right) + 7\left( {z + 1} \right) = 0 \Leftrightarrow 5x - 2y + 7z - 3 = 0\).
b) Một vectơ pháp tuyến của \(\left( P \right)\) là:
\(\vec n = \left[ {\vec u,\vec v} \right] = \left( {2.0 - \left( { - 1} \right).1; - 1.3 - 2.0;2.1 - 2.3} \right) = \left( {1; - 3; - 4} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua \(B\left( { - 2;3;0} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1; - 3; - 4} \right)\) nên có phương trình là \(1\left( {x + 2} \right) - 3\left( {y - 3} \right) - 4\left( {z - 0} \right) = 0 \Leftrightarrow x - 3y - 4z + 11 = 0\).
c) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(A\left( {2;1;5} \right)\), \(B\left( {3;2;7} \right)\), \(C\left( {4;1;6} \right)\) nên có 1 cặp vectơ chỉ phương là \(\overrightarrow {AB} = \left( {1;1;2} \right)\) và \(\overrightarrow {AC} = \left( {2;0;1} \right)\). Do đó một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AC} } \right] = \left( {1.1 - 2.0;2.2 - 1.1;1.0 - 1.2} \right) = \left( {1;3; - 2} \right)\).
Mặt phẳng \(\left( P \right)\) đi qua \(A\left( {2;1;5} \right)\) và có một vectơ pháp tuyến \(\vec n = \left( {1;3; - 2} \right)\) nên có phương trình là \(1\left( {x - 2} \right) + 3\left( {y - 1} \right) - 2\left( {z - 5} \right) = 0 \Leftrightarrow x + 3y - 2z + 5 = 0\).
d) Mặt phẳng \(\left( P \right)\) đi qua ba điểm \(M\left( {7;0;0} \right)\), \(N\left( {0; - 2;0} \right)\), \(P\left( {0;0;9} \right)\) nên phương trình mặt phẳng \(\left( P \right)\) là \(\frac{x}{7} + \frac{y}{{ - 2}} + \frac{z}{9} = 1\).
Trả lời câu hỏi Vận dụng 3 trang 38 SGK Toán 12 Chân trời sáng tạo
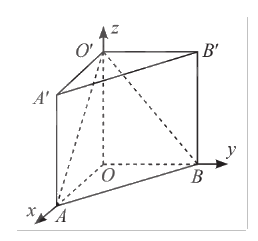
Trong không gian \(Oxyz\), cho hình lăng trụ \(OAB.O'A'B'\). Biết \(O\) là gốc toạ độ, \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\). Viết phương trình các mặt phẳng \(\left( {O'AB} \right)\) và \(\left( {O'A'B'} \right)\).
Phương pháp giải:
Viết phương trình mặt phẳng \(\left( {O'AB} \right)\) dưới dạng phương trình mặt phẳng theo đoạn chắn. Viết phương trình mặt phẳng \(\left( {O'A'B'} \right)\) do nó đi qua điểm \(O'\) và có một vectơ pháp tuyến \(OO'\).
Lời giải chi tiết:
Mặt phẳng \(\left( {O'AB} \right)\) đi qua \(A\left( {2;0;0} \right)\), \(B\left( {0;3;0} \right)\), \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'AB} \right)\) là \(\frac{x}{2} + \frac{y}{3} + \frac{z}{5} = 1\).
Theo hình vẽ, hình lăng trụ \(OAB.O'A'B'\) có các cạnh bên vuông góc với đáy, nên ta có \(OO' \bot \left( {O'A'B'} \right)\). Suy ra \[\overrightarrow {OO'} = \left( {0;0;5} \right)\] là một vectơ pháp tuyến của mặt phẳng \(\left( {O'A'B'} \right)\).
Hơn nữa, mặt phẳng \(\left( {O'A'B'} \right)\) đi qua \(O'\left( {0;0;5} \right)\) nên phương trình mặt phẳng \(\left( {O'A'B'} \right)\) là \(0\left( {x - 0} \right) + 0\left( {y - 0} \right) + 5\left( {z - 5} \right) = 0 \Leftrightarrow z - 5 = 0\).
Giải mục 3 trang 35, 36, 37, 38 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là rất cần thiết để học tốt môn Toán và chuẩn bị cho các kỳ thi sắp tới.
Nội dung chính của Mục 3 (Trang 35-38)
Để hiểu rõ hơn về Mục 3, chúng ta cần xác định nội dung chính mà nó đề cập đến. Thông thường, đây có thể là một dạng toán cụ thể, một định lý quan trọng, hoặc một phương pháp giải toán mới. Hãy xem lại lý thuyết trong SGK để có cái nhìn tổng quan trước khi bắt đầu giải bài tập.
Các bài tập thường gặp trong Mục 3
- Bài tập áp dụng định nghĩa: Các bài tập này yêu cầu bạn hiểu rõ định nghĩa của các khái niệm mới và áp dụng chúng vào các tình huống cụ thể.
- Bài tập chứng minh: Bạn cần sử dụng kiến thức đã học để chứng minh một mệnh đề hoặc một tính chất nào đó.
- Bài tập giải phương trình/bất phương trình: Đây là dạng bài tập phổ biến trong môn Toán, yêu cầu bạn sử dụng các phương pháp giải phương trình/bất phương trình đã học.
- Bài tập thực tế: Các bài tập này liên hệ kiến thức Toán học với các tình huống thực tế, giúp bạn hiểu rõ hơn về ứng dụng của Toán học trong cuộc sống.
Hướng dẫn giải chi tiết các bài tập
Dưới đây là hướng dẫn giải chi tiết cho từng bài tập trong Mục 3, trang 35, 36, 37, 38 SGK Toán 12 tập 2 Chân trời sáng tạo:
Bài 1 (Trang 35)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước giải)
Bài 2 (Trang 36)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước giải)
Bài 3 (Trang 37)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước giải)
Bài 4 (Trang 38)
Đề bài: (Ví dụ về đề bài)
Lời giải: (Giải thích chi tiết từng bước giải)
Mẹo giải nhanh và hiệu quả
Để giải các bài tập trong Mục 3 một cách nhanh chóng và hiệu quả, bạn có thể áp dụng một số mẹo sau:
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài là bước đầu tiên để giải quyết bài toán.
- Phân tích đề bài: Xác định các yếu tố quan trọng trong đề bài và mối quan hệ giữa chúng.
- Chọn phương pháp giải phù hợp: Dựa vào đặc điểm của bài toán để chọn phương pháp giải phù hợp nhất.
- Kiểm tra lại kết quả: Sau khi giải xong bài toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo thêm
Ngoài SGK, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 12:
- Sách bài tập Toán 12: Cung cấp nhiều bài tập luyện tập khác nhau.
- Các trang web học Toán trực tuyến: Cung cấp các bài giảng, bài tập và lời giải chi tiết.
- Các video hướng dẫn giải Toán: Giúp bạn hiểu rõ hơn về các khái niệm và phương pháp giải toán.
Tusach.vn hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ giải quyết thành công các bài tập trong Mục 3, trang 35, 36, 37, 38 SGK Toán 12 tập 2 Chân trời sáng tạo và đạt kết quả tốt nhất trong học tập!