Đề bài
Kết quả khảo sát năng suất (đơn vị: tấn/ha) của một số thửa ruộng được minh hoạ ở biểu đồ sau.
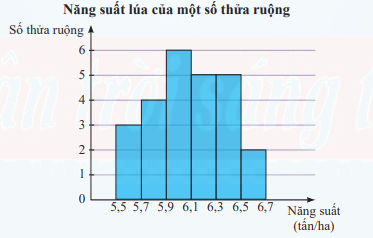a) Có bao nhiêu thửa ruộng đã được khảo sát? b) Lập bảng tần số ghép nhóm và tần số tương đối ghép nhóm tương ứng của mẫu số liệu trên. c) Hãy xác định khoảng biến thiên, khoảng tứ phân vị và độ lệch chuẩn của mẫu số liệu trên.
Phương pháp giải - Xem chi tiết
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Phương sai của mẫu số liệu ghép nhóm, kí hiệu \({S^2}\), được tính bởi công thức:
\({S^2} = \frac{1}{n}[{n_1}{({c_1} - \overline x )^2} + {n_2}{({c_2} - \overline x )^2} + ... + {n_k}{({c_k} - \overline x )^2}]\)
Trong đó: \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu
\(\overline x = \frac{1}{n}({n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k})\) là số trung bình
Độ lệch chuẩn của mẫu số liệu ghép nhóm, kí hiệu \(S\), là căn bậc hai số học của phương sai.
Lời giải chi tiết
a) Có 3 + 4 + 6 + 5 + 5 + 2 = 25 thửa ruộng đã được khảo sát
b)
c) Khoảng biến thiên của mẫu số liệu là: 6,7 – 5,5 = 1,2 (tấn/ha)
Cỡ mẫu \(n = 25\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}}\) là mẫu số liệu gốc về năng suất của 25 thửa ruộng được xếp theo thứ tự không giảm.
Ta có: \({x_1}; \ldots ;{\rm{ }}{x_3} \in [5,5;5,7)\); \({x_4}; \ldots ;{\rm{ }}{x_7} \in [5,7;5,9)\);\({x_8}; \ldots ;{\rm{ }}{x_{13}} \in [5,9;6,1)\);\({x_{14}};...;{x_{18}} \in [6,1;6,3)\);\({x_{19}};...;{x_{23}} \in [6,3;6,5)\);\({x_{24}};{x_{25}} \in [6,5;6,7)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_6};{x_7}) \in [5,7;5,9)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 5,7 + \frac{{\frac{{25}}{4} - 3}}{4}(5,9 - 5,7) = 5,8625\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [6,3;6,5)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 6,3 + \frac{{\frac{{3.25}}{4} - (3 + 4 + 6 + 5)}}{5}(6,5 - 6,3) = 6,33\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 0,4675\)
Số trung bình: \(\overline x = \frac{{3.5,6 + 4.5,8 + 6.6,0 + 5.6,2 + 5.6,4 + 2.6,6}}{{25}} = 6,088\)
Độ lệch chuẩn: \(\sigma = \sqrt {\frac{{{{5.75}^2} + {{10.125}^2} + {{9.175}^2} + {{4.225}^2} + {{2.275}^2}}}{{30}} - {{155}^2}} \approx 0,29\)
