Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo
SGK Toán 12 - Chân trời sáng tạo
Giải Toán 12 tập 1 - Chân trời sáng tạo
Chương 1. Ứng dụng đạo hàm để khảo sát hàm số
Bài 3. Đường tiệm cận của đồ thị hàm số

Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 5 trang 24 SGK Toán 12 tập 1 thuộc chương trình học môn Toán lớp 12, tập trung vào các kiến thức về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng các định nghĩa và tính chất của giới hạn để giải quyết các bài toán cụ thể.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

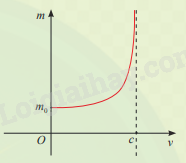
Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động: Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)trong đó \({m_0}\) là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng.

Đề bài

Tìm tiệm cận của đồ thị hàm số khối lượng hạt \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\) trong Khởi động: Theo thuyết tương đối hẹp, khối lượng m (kg) của một hạt phụ thuộc vào tốc độ di chuyển v (km/s) của nó trong hệ quy chiếu quán tính theo công thức \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)trong đó \({m_0}\) là khối lượng nghỉ của hạt, c = 300 000 km/s là tốc độ ánh sáng.

Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

(Theo: https://www.britannica.com/science/relativistic-mass)

Phương pháp giải - Xem chi tiếtGiải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

- Đường thẳng x = a được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau thoả mãn: \(\mathop {\lim f(x) = }\limits_{x \to {a^ - }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} + \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ - }} - \infty ,\mathop {\lim f(x) = }\limits_{x \to {a^ + }} - \infty \)

- Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)

- Đường thẳng y = ax + b, a ≠ 0, được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } [f(x) - (ax + b)] = 0\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } [f(x) - (ax + b)] = 0\)

Lời giải chi tiết

Xét \(m(v) = \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }}\)

Tập xác định: \(D = \mathbb{N}\backslash \{ c\} \)

Ta có: \(\mathop {\lim }\limits_{v \to {c^ + }} m(v) = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ + }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = + \infty \); \(\mathop {\lim }\limits_{v \to {c^ - }} m(v) = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{{m_0}}}{{\sqrt {1 - \frac{{{v^2}}}{{{c^2}}}} }} = \mathop {\lim }\limits_{v \to {c^ - }} \frac{{\frac{{{m_0}}}{v}}}{{\sqrt {\frac{1}{{{v^2}}} - \frac{1}{{{c^2}}}} }} = \frac{{\frac{{{m_0}}}{c}}}{{\sqrt {\frac{1}{{{c^2}}} - \frac{1}{{{c^2}}}} }} = - \infty \)

Vậy đường thẳng x = c là tiệm cận đứng của đồ thị hàm số

Giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học môn Toán lớp 12, tập trung vào việc rèn luyện kỹ năng tính giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về giới hạn, các định lý về giới hạn và các phương pháp tính giới hạn thường gặp.

Nội dung bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 5 thường bao gồm các dạng bài sau:

  • Tính giới hạn của hàm số tại một điểm.
  • Tính giới hạn của hàm số khi x tiến tới vô cùng.
  • Sử dụng các định lý về giới hạn để đơn giản hóa biểu thức và tính giới hạn.

Phương pháp giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Để giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo, bạn có thể áp dụng các phương pháp sau:

  1. Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn (nếu có thể).
  2. Phương pháp phân tích thành nhân tử: Phân tích biểu thức chứa x thành nhân tử để rút gọn và tính giới hạn.
  3. Phương pháp nhân liên hợp: Nhân tử và mẫu số với biểu thức liên hợp để khử dạng vô định.
  4. Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý về giới hạn để tính giới hạn của hàm số.

Lời giải chi tiết bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo

Dưới đây là lời giải chi tiết cho từng phần của bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo:

Ví dụ 1: Tính limx→2 (x2 - 4) / (x - 2)

Lời giải:

Ta có: (x2 - 4) / (x - 2) = (x - 2)(x + 2) / (x - 2) = x + 2 (với x ≠ 2)

Vậy, limx→2 (x2 - 4) / (x - 2) = limx→2 (x + 2) = 2 + 2 = 4

Ví dụ 2: Tính limx→∞ (2x + 1) / (x - 3)

Lời giải:

Ta có: (2x + 1) / (x - 3) = (2 + 1/x) / (1 - 3/x)

Vậy, limx→∞ (2x + 1) / (x - 3) = (2 + 0) / (1 - 0) = 2

Lưu ý khi giải bài tập về giới hạn

  • Luôn kiểm tra xem biểu thức có dạng vô định hay không trước khi tính giới hạn.
  • Sử dụng các định lý về giới hạn một cách chính xác.
  • Rút gọn biểu thức trước khi tính giới hạn để đơn giản hóa bài toán.

Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là một trang web cung cấp đầy đủ các tài liệu học tập môn Toán 12, bao gồm SGK, SBT, đề thi, bài giải và các bài viết hướng dẫn giải bài tập chi tiết. Chúng tôi luôn cập nhật những thông tin mới nhất và cung cấp cho học sinh những tài liệu học tập chất lượng nhất. Hãy truy cập Tusach.vn để học tập và ôn luyện môn Toán 12 hiệu quả!

Hy vọng với hướng dẫn chi tiết này, các bạn học sinh sẽ tự tin hơn khi giải bài tập 5 trang 24 SGK Toán 12 tập 1 - Chân trời sáng tạo và đạt kết quả tốt trong môn học.

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN