Lý Thuyết Biểu Thức Tọa Độ Vectơ Toán 12 Chân Trời Sáng Tạo

Lý thuyết Biểu thức tọa độ của các phép toán vecto Toán 12 Chân trời sáng tạo

Lý thuyết Biểu thức tọa độ của các phép toán vectơ Toán 12 Chân Trời Sáng Tạo

Bài học này cung cấp kiến thức nền tảng về biểu thức tọa độ của các phép toán vectơ trong chương trình Toán 12 Chân Trời Sáng Tạo. Chúng ta sẽ tìm hiểu cách biểu diễn vectơ bằng tọa độ và thực hiện các phép toán cộng, trừ, nhân với một số thực trên vectơ dưới dạng tọa độ.

Nắm vững lý thuyết này là bước quan trọng để giải quyết các bài toán liên quan đến vectơ trong không gian, đặc biệt là trong các bài toán hình học giải tích.

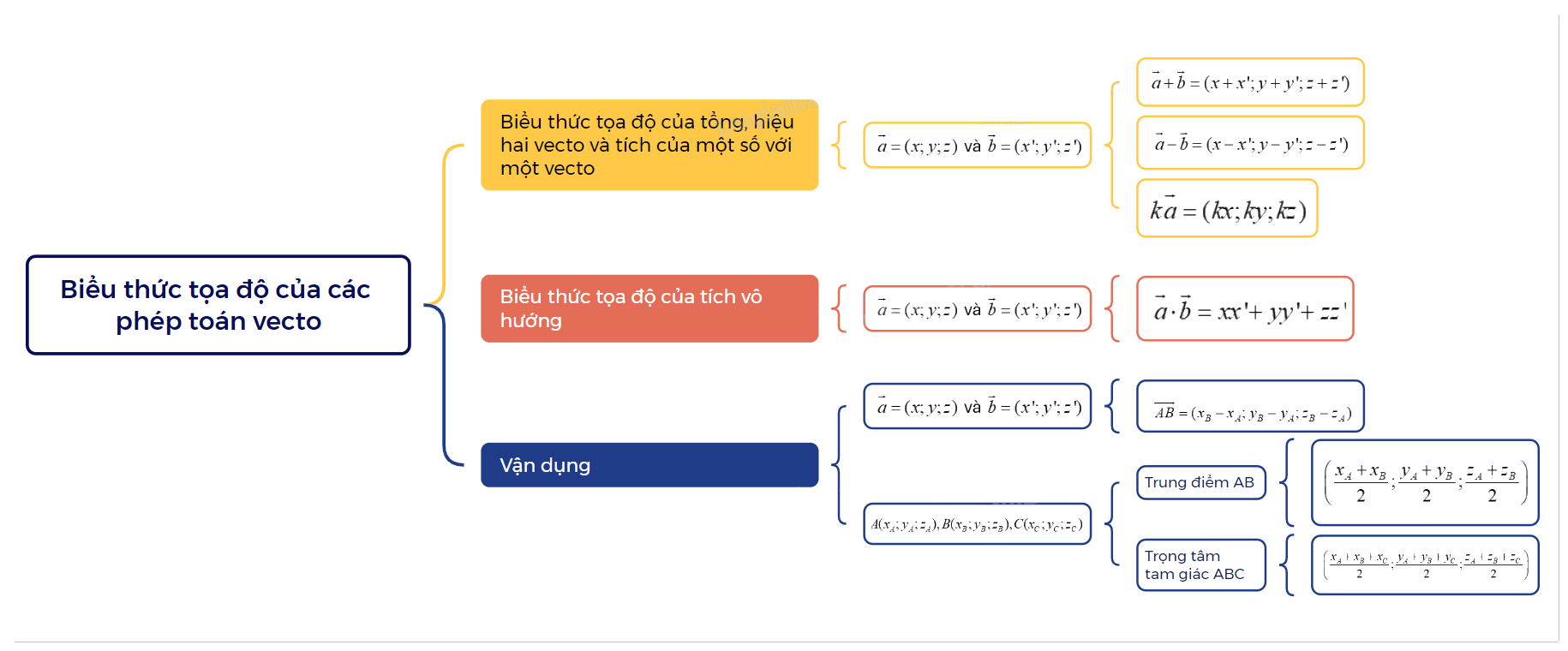
Bài 3. Biểu thức tọa độ của các phép toán vecto 1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

1. Biểu thức tọa độ của tổng, hiệu hai vecto và tích của một số với một vecto

Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\). Ta có:

\(\overrightarrow a + \overrightarrow b = (x + x';y + y';z + z')\)
\(\overrightarrow a - \overrightarrow b = (x - x';y - y';z - z')\)
\(k\overrightarrow a = (kx;ky;kz)\) với k là một số thực

2. Biểu thức tọa độ của tích vô hướng

Trong không gian Oxyz, tích vô hướng của hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x';y';z')\) được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = xx' + yy' + zz'\)

3. Vận dụng

a) Xác định tọa độ của vecto khi biết tọa độ điểm đầu và điểm cuối

Trong không gian Oxyz, cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Ta có:

\(\overrightarrow {AB} = ({x_B} - {x_A};{y_B} - {y_A};{z_B} - {z_A})\)

b) Tọa độ trung điểm đoạn thẳng. Tọa độ trọng tâm tam giác

Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Khi đó:

Tọa độ trung điểm của đoạn thẳng AB là \(\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)\)
Tọa độ trọng tâm tam giác ABC là \(\left( {\frac{{{x_A} + {x_B} + {x_C}}}{2};\frac{{{y_A} + {y_B} + {y_C}}}{2};\frac{{{z_A} + {z_B} + {z_C}}}{2}} \right)\)

Lý Thuyết Biểu Thức Tọa Độ Của Các Phép Toán Vectơ Toán 12 Chân Trời Sáng Tạo

Trong chương trình Toán 12 Chân Trời Sáng Tạo, việc hiểu rõ về biểu thức tọa độ của các phép toán vectơ là vô cùng quan trọng. Nó không chỉ là nền tảng cho việc giải các bài toán hình học giải tích mà còn là bước đệm để tiếp cận các khái niệm toán học nâng cao hơn.

1. Vectơ và Tọa Độ Vectơ

Một vectơ trong không gian được xác định bởi độ dài và hướng của nó. Để biểu diễn vectơ một cách cụ thể, chúng ta sử dụng tọa độ vectơ. Trong mặt phẳng tọa độ Oxy, một vectơ a được biểu diễn bởi cặp số (x; y), trong đó x là hoành độ và y là tung độ của vectơ.

Trong không gian Oxyz, một vectơ a được biểu diễn bởi bộ ba số (x; y; z), trong đó x, y, z lần lượt là hoành độ, tung độ và cao độ của vectơ.

2. Các Phép Toán Vectơ Dưới Dạng Tọa Độ

Khi đã có tọa độ của các vectơ, việc thực hiện các phép toán cộng, trừ, nhân với một số thực trở nên đơn giản hơn rất nhiều.

Phép cộng vectơ: Cho hai vectơ a = (x₁; y₁) và b = (x₂; y₂). Khi đó, a + b = (x₁ + x₂; y₁ + y₂).
Phép trừ vectơ: Cho hai vectơ a = (x₁; y₁) và b = (x₂; y₂). Khi đó, a - b = (x₁ - x₂; y₁ - y₂).
Phép nhân vectơ với một số thực: Cho vectơ a = (x; y) và một số thực k. Khi đó, ka = (kx; ky).

3. Ví Dụ Minh Họa

Ví dụ 1: Cho a = (2; -3) và b = (-1; 4). Tính a + b và 2a.

Giải:

a + b = (2 + (-1); -3 + 4) = (1; 1)
2a = (2 * 2; 2 * (-3)) = (4; -6)

4. Ứng Dụng của Biểu Thức Tọa Độ Vectơ

Biểu thức tọa độ vectơ có nhiều ứng dụng trong thực tế, đặc biệt trong các lĩnh vực như:

Vật lý: Tính toán vận tốc, gia tốc, lực tác dụng lên vật thể.
Đồ họa máy tính: Xây dựng mô hình 3D, tạo hiệu ứng hình ảnh.
Kỹ thuật: Thiết kế và phân tích các công trình xây dựng, máy móc.

5. Bài Tập Thực Hành

Để củng cố kiến thức, bạn hãy thử giải các bài tập sau:

Cho a = (1; 2) và b = (3; -1). Tính a - b và -3b.
Tìm tọa độ của vectơ c biết rằng c = 2a + b, với a = (-1; 0) và b = (4; 2).

Hy vọng bài viết này đã giúp bạn hiểu rõ hơn về lý thuyết biểu thức tọa độ của các phép toán vectơ Toán 12 Chân Trời Sáng Tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và áp dụng vào giải các bài toán thực tế.