Giải mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 3 trang 72, 73, 74 sách giáo khoa Toán 12 tập 2 chương trình Chân trời sáng tạo.
Chúng tôi giúp bạn nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt nhất trong môn Toán.
Hãy cùng tusach.vn khám phá lời giải ngay nhé!
Ban Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ Nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ Bảy là 0,7. Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:
TH4
Trả lời câu hỏi Thực hành 4 trang 74 SGK Toán 12 Chân trời sáng tạo
Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”.
\(B\): “Hai viên bi lấy ra có cùng màu”.
Phương pháp giải:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( A \right)\) và \(P\left( B \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”.
Xác suất để lấy ra được 1 viên bi xanh ở hộp thứ nhất là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi xanh ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 6 viên bi xanh và 4 viên bi đỏ. Suy ra xác suất để lấy ra được 1 viên bi đỏ là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi đỏ ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 5 viên bi xanh và 5 viên bi đỏ. Suy ra xác suất để lấy được 1 viên bi đỏ là \(\frac{5}{{10}} = 0,5\).
Ta có sơ đồ hình cây sau:
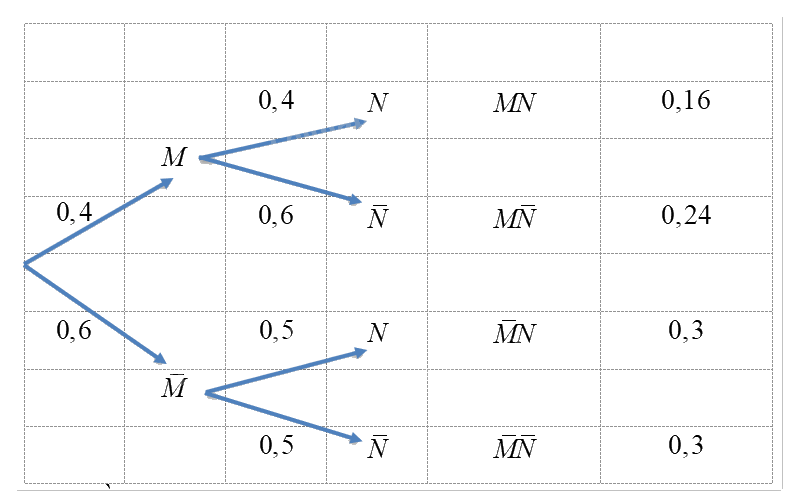
Dựa vào sơ đồ hình cây, ta có:
\(P\left( A \right) = P\left( {MN} \right) = 0,16.\)
\(P\left( B \right) = P\left( {M\bar N} \right) + P\left( {\bar MN} \right) = 0,24 + 0,3 = 0,54.\)
VD3
Trả lời câu hỏi Vận dụng 3 trang 74 SGK Toán 12 Chân trời sáng tạo
Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là 85% đối với sinh viên loại giỏi và 70% đối với sinh viên tốt nghiệp loại khác.
Tỉ lệ sinh viên tốt nghiệp loại giỏi là 30%. Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(C\): “Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
\(D\): “Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
Phương pháp giải:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( C \right)\) và \(P\left( D \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”.
Theo đề bài, ta có sơ đồ hình cây sau:

Từ sơ đồ hình cây, ta suy ra \(P\left( C \right) = P\left( {MN} \right) = 0,255\) và \(P\left( D \right) = P\left( {\bar MN} \right) = 0,49.\)
HĐ3
Trả lời câu hỏi Hoạt động 3 trang 72 SGK Toán 12 Chân trời sáng tạo
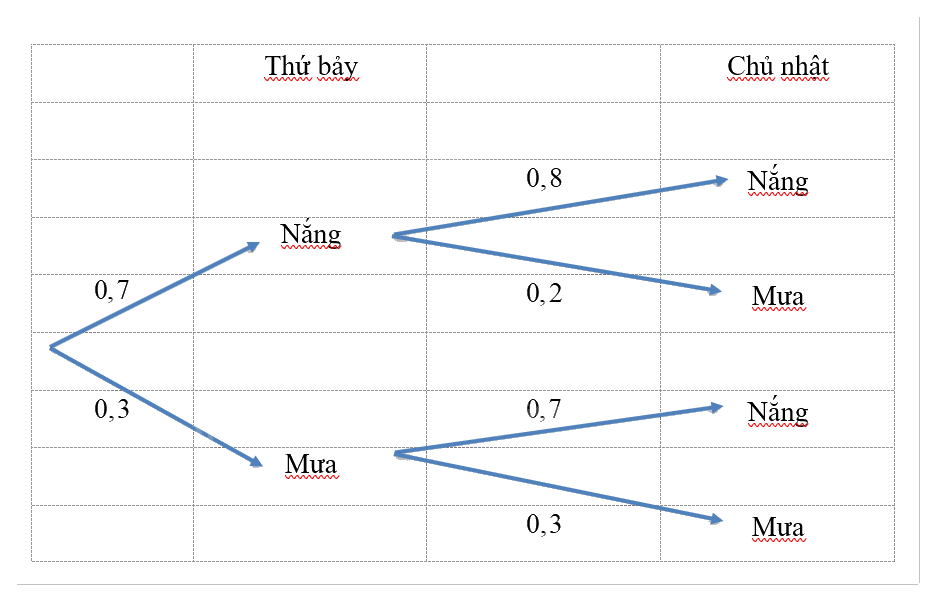
Ban Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ Nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ Bảy là 0,7.
Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:
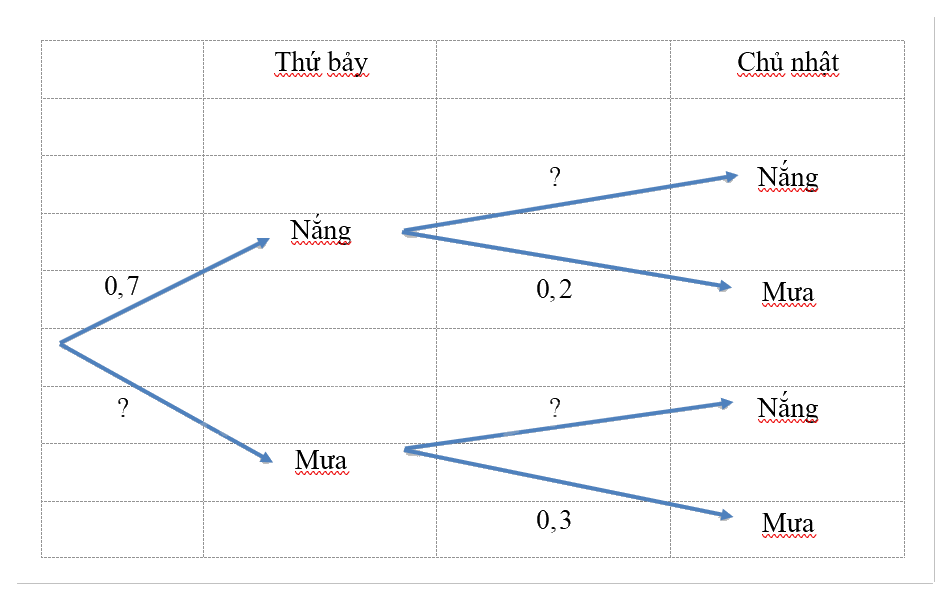
Phương pháp giải:
Do trong một ngày chỉ có thể xảy ra biến cố “Trời nắng” hoặc “Trời mưa”, nên sử dụng công thức cộng xác suất với các biến cố đối để điền các số vào dấu hỏi chấm.
Lời giải chi tiết:
Với ngày thứ 7, xác suất trời nắng là \(0,7\) nên xác suất trời mưa là \(1 - 0,7 = 0,3\).
Với ngày Chủ nhật:
- Trong trường hợp ngày thứ 7 trời nắng, xác suất trời mưa trong ngày Chủ nhật là \(0,2\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,2 = 0,8\).
- Trong trường hợp ngày thứ 7 trời mưa, xác suất trời mưa trong ngày Chủ nhật là \(0,3\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,3 = 0,7\).
Ta có sơ đồ sau:
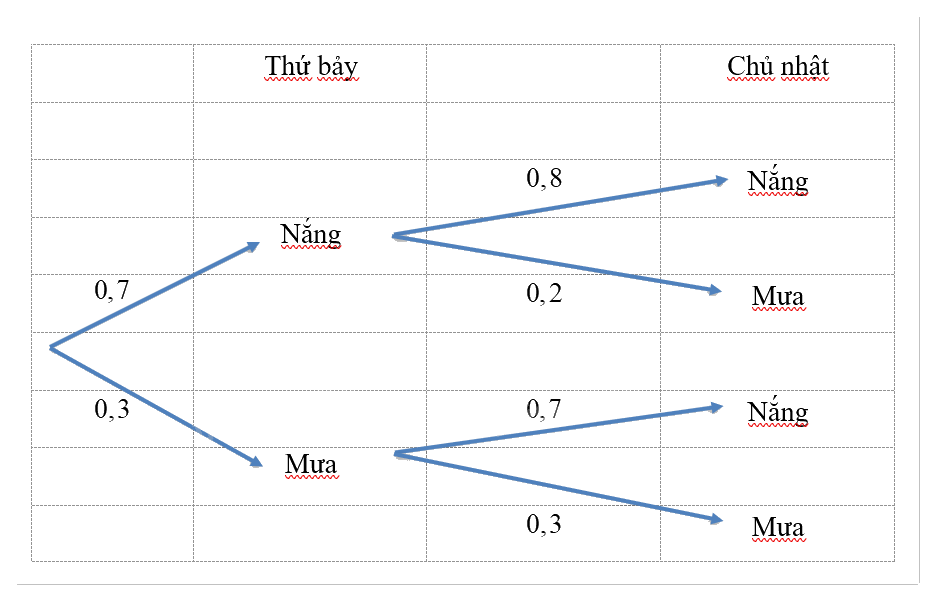
- HĐ3
- TH4
- VD3
Trả lời câu hỏi Hoạt động 3 trang 72 SGK Toán 12 Chân trời sáng tạo
Ban Việt chuẩn bị đi tham quan một hòn đảo trong hai ngày thứ Bảy và Chủ Nhật. Ở hòn đảo đó, mỗi ngày chỉ có nắng hoặc mưa, nếu một ngày là nắng thì khả năng xảy ra mưa ở ngày tiếp theo là 20%, còn nếu một ngày là mưa thì khả năng ngày hôm sau vẫn mưa là 30%. Theo dự báo thời tiết, xác suất trời sẽ nắng vào ngày thứ Bảy là 0,7.
Hãy tìm các giá trị thích hợp thay vào ? ở sơ đồ hình cây sau:
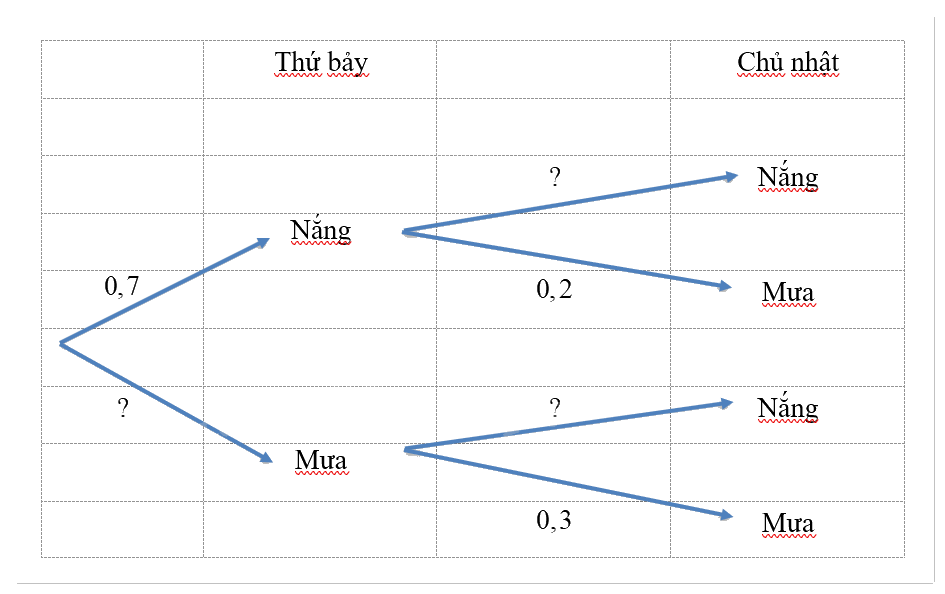
Phương pháp giải:
Do trong một ngày chỉ có thể xảy ra biến cố “Trời nắng” hoặc “Trời mưa”, nên sử dụng công thức cộng xác suất với các biến cố đối để điền các số vào dấu hỏi chấm.
Lời giải chi tiết:
Với ngày thứ 7, xác suất trời nắng là \(0,7\) nên xác suất trời mưa là \(1 - 0,7 = 0,3\).
Với ngày Chủ nhật:
- Trong trường hợp ngày thứ 7 trời nắng, xác suất trời mưa trong ngày Chủ nhật là \(0,2\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,2 = 0,8\).
- Trong trường hợp ngày thứ 7 trời mưa, xác suất trời mưa trong ngày Chủ nhật là \(0,3\). Suy ra xác suất trời nắng trong ngày Chủ nhật là \(1 - 0,3 = 0,7\).
Ta có sơ đồ sau:
Trả lời câu hỏi Thực hành 4 trang 74 SGK Toán 12 Chân trời sáng tạo
Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên 1 viên bi từ hộp thứ hai. Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(A\): “Viên bi lấy ra từ hộp thứ nhất có màu xanh và viên bi lấy ra từ hộp thứ hai có màu đỏ”.
\(B\): “Hai viên bi lấy ra có cùng màu”.
Phương pháp giải:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( A \right)\) và \(P\left( B \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Viên bi lấy ra ở hộp thứ nhất có màu xanh” và \(N\) là biến cố “Viên bi lấy ra ở hộp thứ hai có màu đỏ”.
Xác suất để lấy ra được 1 viên bi xanh ở hộp thứ nhất là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi xanh ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 6 viên bi xanh và 4 viên bi đỏ. Suy ra xác suất để lấy ra được 1 viên bi đỏ là \(\frac{4}{{10}} = 0,4\).
Nếu ta lấy được viên bi đỏ ở hộp thứ nhất và bỏ vào hộp thứ hai thì hộp thứ hai có 5 viên bi xanh và 5 viên bi đỏ. Suy ra xác suất để lấy được 1 viên bi đỏ là \(\frac{5}{{10}} = 0,5\).
Ta có sơ đồ hình cây sau:
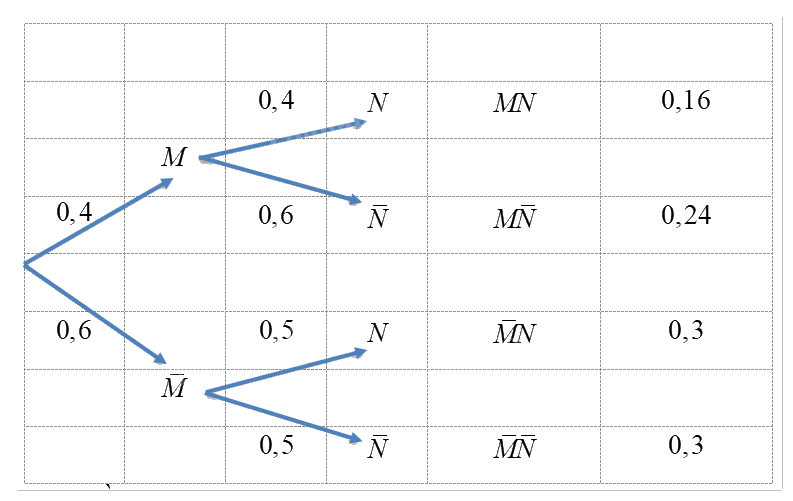
Dựa vào sơ đồ hình cây, ta có:
\(P\left( A \right) = P\left( {MN} \right) = 0,16.\)
\(P\left( B \right) = P\left( {M\bar N} \right) + P\left( {\bar MN} \right) = 0,24 + 0,3 = 0,54.\)
Trả lời câu hỏi Vận dụng 3 trang 74 SGK Toán 12 Chân trời sáng tạo
Một trường đại học tiến hành khảo sát tình trạng việc làm sau khi tốt nghiệp của sinh viên. Kết quả khảo sát cho thấy tỉ lệ người tìm được việc làm đúng chuyên ngành là 85% đối với sinh viên loại giỏi và 70% đối với sinh viên tốt nghiệp loại khác.
Tỉ lệ sinh viên tốt nghiệp loại giỏi là 30%. Gặp ngẫu nhiên một sinh viên đã tốt nghiệp của trường.
Sử dụng sơ đồ hình cây, tính xác suất của các biến cố:
\(C\): “Sinh viên tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
\(D\): “Sinh viên không tốt nghiệp loại giỏi và tìm được việc làm đúng chuyên ngành”.
Phương pháp giải:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”. Sử dụng sơ đồ hình cây, từ đó tính được \(P\left( C \right)\) và \(P\left( D \right)\).
Lời giải chi tiết:
Gọi \(M\) là biến cố “Sinh viên tốt nghiệp loại giỏi” và \(N\) là biến cố “Sinh viên tìm được việc làm đúng chuyên ngành”.
Theo đề bài, ta có sơ đồ hình cây sau:

Từ sơ đồ hình cây, ta suy ra \(P\left( C \right) = P\left( {MN} \right) = 0,255\) và \(P\left( D \right) = P\left( {\bar MN} \right) = 0,49.\)
Giải mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 3 trong SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường xoay quanh các chủ đề về Đường thẳng và mặt phẳng trong không gian, bao gồm các kiến thức về quan hệ song song, vuông góc giữa đường thẳng và mặt phẳng, góc giữa hai mặt phẳng, và khoảng cách từ một điểm đến mặt phẳng. Việc nắm vững kiến thức này là nền tảng quan trọng để giải quyết các bài toán hình học không gian phức tạp hơn.
Nội dung chính của Mục 3 trang 72, 73, 74
- Bài tập 1: Thường tập trung vào việc xác định vị trí tương đối giữa đường thẳng và mặt phẳng, sử dụng các định lý và tính chất đã học.
- Bài tập 2: Liên quan đến việc tính góc giữa hai mặt phẳng, đòi hỏi học sinh phải vận dụng kiến thức về vector pháp tuyến và công thức tính góc.
- Bài tập 3: Thực hành tính khoảng cách từ một điểm đến mặt phẳng, sử dụng công thức và các bước giải cụ thể.
Lời giải chi tiết các bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 3 trang 72, 73, 74 SGK Toán 12 tập 2 - Chân trời sáng tạo:
Bài tập 1: (Trang 72)
Đề bài: (Ví dụ: Cho hình chóp S.ABCD, đáy là hình vuông ABCD. Gọi M là trung điểm của CD. Chứng minh rằng AM vuông góc với BM.)
Lời giải:
- Chọn hệ tọa độ thích hợp với A là gốc tọa độ, AB là trục x, AD là trục y, AS là trục z.
- Xác định tọa độ các điểm A, B, C, D, M.
- Tính vector AM và BM.
- Chứng minh AM.BM = 0, suy ra AM vuông góc với BM.
Bài tập 2: (Trang 73)
Đề bài: (Ví dụ: Tính góc giữa hai mặt phẳng (SBC) và (ABCD) của hình chóp S.ABCD, biết SA vuông góc với mặt phẳng (ABCD).)
Lời giải:
- Xác định vector pháp tuyến của mặt phẳng (SBC) và (ABCD).
- Sử dụng công thức tính góc giữa hai mặt phẳng: cos(θ) = |n1.n2| / (|n1| * |n2|).
- Tính toán và tìm ra giá trị của θ.
Bài tập 3: (Trang 74)
Đề bài: (Ví dụ: Tính khoảng cách từ điểm A đến mặt phẳng (SCD) của hình chóp S.ABCD, biết SA vuông góc với mặt phẳng (ABCD).)
Lời giải:
- Tìm phương trình mặt phẳng (SCD).
- Sử dụng công thức tính khoảng cách từ một điểm đến mặt phẳng: d = |Ax0 + By0 + Cz0 + D| / √(A² + B² + C²).
- Thay tọa độ điểm A và các hệ số của phương trình mặt phẳng vào công thức để tính khoảng cách.
Mẹo giải nhanh và hiệu quả
- Nắm vững kiến thức lý thuyết: Hiểu rõ các định lý, tính chất và công thức liên quan đến đường thẳng và mặt phẳng trong không gian.
- Vẽ hình minh họa: Vẽ hình giúp bạn hình dung rõ hơn về bài toán và tìm ra hướng giải quyết.
- Chọn hệ tọa độ phù hợp: Việc chọn hệ tọa độ hợp lý sẽ giúp đơn giản hóa các phép tính và giải quyết bài toán nhanh chóng hơn.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập môn Toán 12. Chúng tôi cung cấp đầy đủ lời giải chi tiết, bài giảng video, và các tài liệu học tập hữu ích khác. Hãy truy cập tusach.vn để học Toán 12 hiệu quả và đạt kết quả tốt nhất!