Giải bài tập 11 trang 38 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải Bài Tập 11 Trang 38 Toán 12 Tập 1 - Chân Trời Sáng Tạo
Chào mừng bạn đến với lời giải chi tiết bài tập 11 trang 38 SGK Toán 12 tập 1 Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, hỗ trợ tối đa cho quá trình học tập của bạn.
Cho hàm số (y = frac{1}{3}{x^3} - {x^2} + 4). a) Khảo sát và vẽ đồ thị của hàm số. b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.
Đề bài
Cho hàm số \(y = \frac{1}{3}{x^3} - {x^2} + 4\).
a) Khảo sát và vẽ đồ thị của hàm số.
b) Tính khoảng cách giữa hai điểm cực trị của đồ thị hàm số.
Phương pháp giải - Xem chi tiết
a) Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu, cực trị (nếu có) của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực của hàm số và các đường tiệm cận của đồ thị hàm số (nếu có).
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các điểm cực trị (nếu có), giao điểm của đồ thị với các trục toạ độ (nếu có và dễ tìm), ...
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
b) Quan sát đồ thị và tìm khoảng cách giữa 2 cực trị. Dùng định lí Pytago để tìm khoảng cách đó
Lời giải chi tiết
a) Tập xác định: \(D = \mathbb{R}\)
- Chiều biến thiên:
\(y' = {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)
Trên các khoảng (\( - \infty \); 0), (2; \( + \infty \)) thì y' < 0 nên hàm số nghịch biến trên mỗi khoảng đó. Trên khoảng (0; 2) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị:
Hàm số đạt cực đại tại x = 0 và \({y_{cd}} = 4\)
Hàm số đạt cực tiểu tại x = 2 và \({y_{ct}} = \frac{8}{3}\)
- Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (\frac{1}{3}{x^3} - {x^2} + 4) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (\frac{1}{3}{x^3} - {x^2} + 4) = + \infty \)
- Bảng biến thiên:
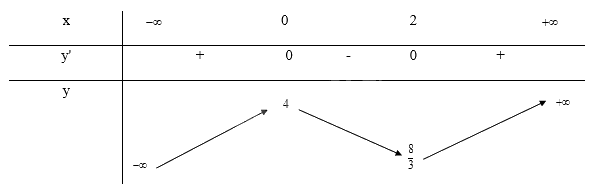
Khi x = 0 thì y = 4 nên (0; 4) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{1}{3}{x^3} - {x^2} + 4 = 0 \Leftrightarrow x = - 1,61\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1,61; 0)
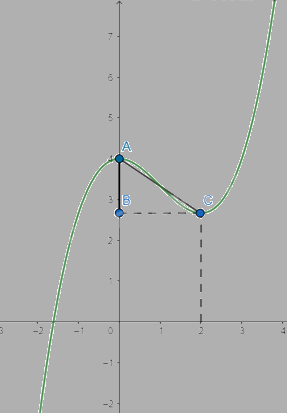
b) Khoảng cách giữa 2 cực trị là \(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{(4 - 8/3)}^2} + {2^2}} \)
= \(\frac{{2\sqrt {13} }}{3}\)
Giải Bài Tập 11 Trang 38 Toán 12 Tập 1 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết
Bài tập 11 trang 38 SGK Toán 12 tập 1 Chân trời sáng tạo thuộc chương trình học về đạo hàm. Đây là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm của hàm số và ứng dụng đạo hàm để giải quyết các bài toán thực tế.
Nội Dung Bài Tập 11 Trang 38
Bài tập yêu cầu tính đạo hàm của các hàm số sau:
- a) y = x4 + 5x2 + 3
- b) y = 2x3 - x + 1
- c) y = (x2 + 1)(x - 2)
- d) y = (x2 + 3x)(x2 - 2x + 5)
Phương Pháp Giải
Để giải bài tập này, chúng ta cần nắm vững các quy tắc tính đạo hàm cơ bản sau:
- Đạo hàm của một tổng: (u + v)' = u' + v'
- Đạo hàm của một tích: (uv)' = u'v + uv'
- Đạo hàm của một hàm số lũy thừa: (xn)' = nxn-1
- Đạo hàm của một hằng số: (c)' = 0
Lời Giải Chi Tiết
a) y = x4 + 5x2 + 3
y' = (x4)' + (5x2)' + (3)' = 4x3 + 10x + 0 = 4x3 + 10x
b) y = 2x3 - x + 1
y' = (2x3)' - (x)' + (1)' = 6x2 - 1 + 0 = 6x2 - 1
c) y = (x2 + 1)(x - 2)
y' = (x2 + 1)'(x - 2) + (x2 + 1)(x - 2)' = (2x)(x - 2) + (x2 + 1)(1) = 2x2 - 4x + x2 + 1 = 3x2 - 4x + 1
d) y = (x2 + 3x)(x2 - 2x + 5)
y' = (x2 + 3x)'(x2 - 2x + 5) + (x2 + 3x)(x2 - 2x + 5)' = (2x + 3)(x2 - 2x + 5) + (x2 + 3x)(2x - 2)
= (2x3 - 4x2 + 10x + 3x2 - 6x + 15) + (2x3 - 2x2 + 6x2 - 6x)
= 2x3 - x2 + 4x + 15 + 2x3 + 4x2 - 6x
= 4x3 + 3x2 - 2x + 15
Lưu Ý Khi Giải Bài Tập
- Nắm vững các quy tắc tính đạo hàm cơ bản.
- Áp dụng đúng quy tắc khi tính đạo hàm của các hàm số phức tạp.
- Kiểm tra lại kết quả sau khi tính toán.
Tusach.vn - Đồng Hành Cùng Bạn Trên Con Đường Học Tập
Tusach.vn luôn cập nhật lời giải chi tiết các bài tập trong SGK Toán 12 tập 1 Chân trời sáng tạo. Hãy truy cập website của chúng tôi để tìm hiểu thêm và nâng cao kiến thức của bạn.
Chúc bạn học tập tốt!