Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Chúng tôi giúp học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán hiệu quả.
Với đội ngũ giáo viên giàu kinh nghiệm, các lời giải của chúng tôi không chỉ cung cấp đáp án mà còn giải thích rõ ràng từng bước, giúp bạn hiểu sâu sắc bản chất của bài toán.
Trong không gian (Oxyz), cho mặt cầu (Sleft( {I;R} right)) có tâm (Ileft( {a;b;c} right)) và bán kính (R). Xét một điểm (Mleft( {x;y;z} right)) thay đổi. a) Tính khoảng cách (IM) theo (x), (y), (z) và (a), (b), (c). b) Nêu điều kiện cần và đủ của (x), (y), (z) để điểm (Mleft( {x;y;z} right)) nằm trên mặt cầu (Sleft( {I;R} right)).
TH1
Trả lời câu hỏi Thực hành 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\):
a) Có tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\).
b) Có đường kính \(EF\) với \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\).
c) Có tâm \(M\left( { - 2;1;3} \right)\) và đi qua điểm \(N\left( {2; - 3; - 4} \right)\).
Phương pháp giải:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) có phương trình là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
Lời giải chi tiết:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\) có phương trình là
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 4} \right)^2} = 100\).
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\).
Ta có \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\), suy ra \(I\left( {5; - 2;4} \right)\).
Ta có \(EF = \sqrt {{{\left( {3 - 7} \right)}^2} + {{\left( { - 1 + 3} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = 2\sqrt {21} \), suy ra \(R = \frac{{EF}}{2} = \sqrt {21} \).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 21\).
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\).
Ta có \(MN = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {1 + 3} \right)}^2} + {{\left( {3 + 4} \right)}^2}} = 9\).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 81\).
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 63 SGK Toán 12 Chân trời sáng tạo
a) Trong không gian \(Oxyz\), cho điểm \(M\left( {x;y;z} \right)\) thay đổi có toạ độ luôn thoả mãn phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\). (*)
i) Biến đổi (*) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Chứng tỏ \(M\left( {x;y;z} \right)\) luôn thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\)
b) Bằng cách biến đổi phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\) (**) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\), hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không.
Phương pháp giải:
a) Sử dụng các hằng đẳng thức để đưa phương trình (*) về dạng như đề bài yêu cầu, từ đó suy ra điểm \(M\) luôn thuộc mặt cầu \(\left( S \right)\).
b) Sử dụng hằng đẳng thức để đưa phương trình (**) về dạng như đề bài yêu cầu, rồi kết luận.
Lời giải chi tiết:
a)
i) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) - 25 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\end{array}.\)
ii) Do điểm \(M\left( {x;y;z} \right)\) có toạ độ thoả mãn phương trình (*), suy ra điểm \(M\) thoả mãn phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\). Vậy điểm \(M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) + 1 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\end{array}.\)
Do \( - 1 < 0\), nên phương trình trên không là phương trình mặt cầu. Suy ra (**) không là phương trình mặt cầu.
TH2
Trả lời câu hỏi Thực hành 2 trang 63 SGK Toán 12 Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\)
b) \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\)
Phương pháp giải:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\). Xác định \(a\), \(b\), \(c\), \(d\) và tính \({a^2} + {b^2} + {c^2} - d\), rồi rút ra kết luận.
Lời giải chi tiết:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\).
a) Với phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\), ta có \(a = 0\), \(b = 0\), \(c = - 2\) và \(d = - 32\).
Ta có \({a^2} + {b^2} + {c^2} - d = {0^2} + {0^2} + {\left( { - 2} \right)^2} + 32 = 36 > 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\) là phương trình mặt cầu tâm \(I\left( {0;0; - 2} \right)\) và bán kính \(R = 6\).
b) Với phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\), ta có \(a = - 1\), \(b = - 1\), \(c = 1\) và \(d = 4\).
Ta có \({a^2} + {b^2} + {c^2} - d = {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {1^2} - 4 = - 1 < 0.\)
Vậy phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\) không là phương trình mặt cầu.
VD1
Trả lời câu hỏi Vận dụng 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị của các trục toạ độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\). Tìm toạ độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình \(z = 0\).

Phương pháp giải:
Từ phương trình mặt cầu, chỉ ra tâm và bán kính của quả bóng thám không. Sau đó sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính khoảng cách từ tâm của quả bóng đến mặt đất.
Lời giải chi tiết:
Phương trình bề mặt của quả bóng thám không là \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\), suy ra quả bóng có tâm \(I\left( {300;400;2000} \right)\) và bán kính \(R = 1.\)
Khoảng cách từ tâm quả bóng đến mặt đất là
\(d = \frac{{\left| {0.300 + 0.400 + 1.2000 + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2000\) (mét).
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo
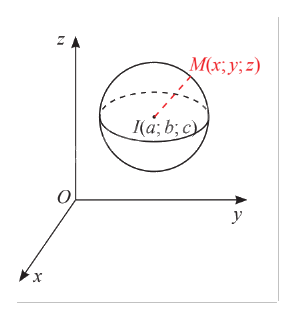
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải chi tiết:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
- HĐ1
- TH1
- VD1
- HĐ2
- TH2
Trả lời câu hỏi Hoạt động 1 trang 61 SGK Toán 12 Chân trời sáng tạo
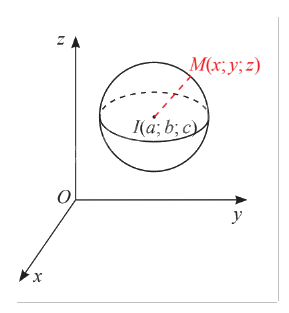
Trong không gian \(Oxyz\), cho mặt cầu \(S\left( {I;R} \right)\) có tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\). Xét một điểm \(M\left( {x;y;z} \right)\) thay đổi.
a) Tính khoảng cách \(IM\) theo \(x\), \(y\), \(z\) và \(a\), \(b\), \(c\).
b) Nêu điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\).
Phương pháp giải:
a) Sử dụng công thức tính khoảng cách giữa hai điểm trong không gian để tính khoảng cách \(IM\).
b) Để điểm \(M\) nằm trên mặt cầu \(S\left( {I;R} \right)\) thì \(IM = R\).
Lời giải chi tiết:
a) Ta có \(I\left( {a;b;c} \right)\) và \(M\left( {x;y;z} \right)\). Suy ra \(IM = \sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} \).
b) Điều kiện cần và đủ của \(x\), \(y\), \(z\) để điểm \(M\left( {x;y;z} \right)\) nằm trên mặt cầu \(S\left( {I;R} \right)\) là \(IM = R\), điều này tương đương với
\(\sqrt {{{\left( {x - a} \right)}^2} + {{\left( {y - b} \right)}^2} + {{\left( {z - c} \right)}^2}} = R \Leftrightarrow {\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\).
Trả lời câu hỏi Thực hành 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Viết phương trình mặt cầu \(\left( S \right)\):
a) Có tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\).
b) Có đường kính \(EF\) với \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\).
c) Có tâm \(M\left( { - 2;1;3} \right)\) và đi qua điểm \(N\left( {2; - 3; - 4} \right)\).
Phương pháp giải:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {a;b;c} \right)\) và bán kính \(R\) có phương trình là
\({\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\)
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\), từ đó viết phương trình mặt cầu \(\left( S \right)\) theo như câu a.
Lời giải chi tiết:
a) Mặt cầu \(\left( S \right)\) tâm \(I\left( {3; - 2; - 4} \right)\), bán kính \(R = 10\) có phương trình là
\({\left( {x - 3} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z + 4} \right)^2} = 100\).
b) Mặt cầu \(\left( S \right)\) có đường kính \(EF\), suy ra \(\left( S \right)\) có tâm \(I\) là trung điểm của \(EF\) và bán kính bằng \(\frac{{EF}}{2}\).
Ta có \(E\left( {3; - 1;8} \right)\) và \(F\left( {7; - 3;0} \right)\), suy ra \(I\left( {5; - 2;4} \right)\).
Ta có \(EF = \sqrt {{{\left( {3 - 7} \right)}^2} + {{\left( { - 1 + 3} \right)}^2} + {{\left( {8 - 0} \right)}^2}} = 2\sqrt {21} \), suy ra \(R = \frac{{EF}}{2} = \sqrt {21} \).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} + {\left( {z - 4} \right)^2} = 21\).
c) Mặt cầu \(\left( S \right)\) có tâm \(M\) và đi qua \(N\), nên \(MN\) là một bán kính của \(\left( S \right)\).
Ta có \(MN = \sqrt {{{\left( { - 2 - 2} \right)}^2} + {{\left( {1 + 3} \right)}^2} + {{\left( {3 + 4} \right)}^2}} = 9\).
Vậy phương trình mặt cầu \(\left( S \right)\) là \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} + {\left( {z - 3} \right)^2} = 81\).
Trả lời câu hỏi Vận dụng 1 trang 62 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\) (đơn vị của các trục toạ độ là mét), các nhà nghiên cứu khí tượng dùng một phần mềm mô phỏng bề mặt của một quả bóng thám không có dạng hình cầu bằng phương trình \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\). Tìm toạ độ tâm, bán kính của quả bóng và tính khoảng cách từ tâm của quả bóng đến mặt đất có phương trình \(z = 0\).

Phương pháp giải:
Từ phương trình mặt cầu, chỉ ra tâm và bán kính của quả bóng thám không. Sau đó sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng để tính khoảng cách từ tâm của quả bóng đến mặt đất.
Lời giải chi tiết:
Phương trình bề mặt của quả bóng thám không là \({\left( {x - 300} \right)^2} + {\left( {y - 400} \right)^2} + {\left( {z - 2000} \right)^2} = 1\), suy ra quả bóng có tâm \(I\left( {300;400;2000} \right)\) và bán kính \(R = 1.\)
Khoảng cách từ tâm quả bóng đến mặt đất là
\(d = \frac{{\left| {0.300 + 0.400 + 1.2000 + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 2000\) (mét).
Trả lời câu hỏi Hoạt động 2 trang 63 SGK Toán 12 Chân trời sáng tạo
a) Trong không gian \(Oxyz\), cho điểm \(M\left( {x;y;z} \right)\) thay đổi có toạ độ luôn thoả mãn phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\). (*)
i) Biến đổi (*) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\).
ii) Chứng tỏ \(M\left( {x;y;z} \right)\) luôn thuộc một mặt cầu \(\left( S \right)\). Tìm tâm và bán kính của \(\left( S \right)\)
b) Bằng cách biến đổi phương trình \({x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\) (**) về dạng \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\), hãy cho biết phương trình (**) có thể là phương trình mặt cầu hay không.
Phương pháp giải:
a) Sử dụng các hằng đẳng thức để đưa phương trình (*) về dạng như đề bài yêu cầu, từ đó suy ra điểm \(M\) luôn thuộc mặt cầu \(\left( S \right)\).
b) Sử dụng hằng đẳng thức để đưa phương trình (**) về dạng như đề bài yêu cầu, rồi kết luận.
Lời giải chi tiết:
a)
i) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z - 11 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) - 25 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\end{array}.\)
ii) Do điểm \(M\left( {x;y;z} \right)\) có toạ độ thoả mãn phương trình (*), suy ra điểm \(M\) thoả mãn phương trình \({\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = 25\). Vậy điểm \(M\) thuộc mặt cầu \(\left( S \right)\) có tâm \(I\left( {1;2;3} \right)\) và bán kính \(R = \sqrt {25} = 5\).
b) Ta có
\(\begin{array}{l}{x^2} + {y^2} + {z^2} - 2x - 4y - 6z + 15 = 0\\ \Leftrightarrow \left( {{x^2} - 2x + 1} \right) + \left( {{y^2} - 4y + 4} \right) + \left( {{z^2} - 6z + 9} \right) + 1 = 0\\ \Leftrightarrow {\left( {x - 1} \right)^2} + {\left( {y - 2} \right)^2} + {\left( {z - 3} \right)^2} = - 1\end{array}.\)
Do \( - 1 < 0\), nên phương trình trên không là phương trình mặt cầu. Suy ra (**) không là phương trình mặt cầu.
Trả lời câu hỏi Thực hành 2 trang 63 SGK Toán 12 Chân trời sáng tạo
Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính của mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\)
b) \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\)
Phương pháp giải:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\). Xác định \(a\), \(b\), \(c\), \(d\) và tính \({a^2} + {b^2} + {c^2} - d\), rồi rút ra kết luận.
Lời giải chi tiết:
Các phương trình ở câu a và b đều là phương trình mặt cầu có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\).
a) Với phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\), ta có \(a = 0\), \(b = 0\), \(c = - 2\) và \(d = - 32\).
Ta có \({a^2} + {b^2} + {c^2} - d = {0^2} + {0^2} + {\left( { - 2} \right)^2} + 32 = 36 > 0\).
Vậy phương trình \({x^2} + {y^2} + {z^2} + 4z - 32 = 0\) là phương trình mặt cầu tâm \(I\left( {0;0; - 2} \right)\) và bán kính \(R = 6\).
b) Với phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\), ta có \(a = - 1\), \(b = - 1\), \(c = 1\) và \(d = 4\).
Ta có \({a^2} + {b^2} + {c^2} - d = {\left( { - 1} \right)^2} + {\left( { - 1} \right)^2} + {1^2} - 4 = - 1 < 0.\)
Vậy phương trình \({x^2} + {y^2} + {z^2} + 2x + 2y - 2z + 4 = 0\) không là phương trình mặt cầu.
Giải mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là vô cùng cần thiết để học sinh có thể đạt kết quả tốt trong các bài kiểm tra và kỳ thi sắp tới. Tusach.vn xin giới thiệu lời giải chi tiết cho các bài tập trang 61, 62, 63, giúp các em học sinh tự tin hơn trong quá trình học tập.
Nội dung chính của Mục 1 (Trang 61, 62, 63)
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của Mục 1. Thông thường, mục này sẽ bao gồm:
- Các khái niệm cơ bản: Định nghĩa, tính chất, các công thức liên quan đến chủ đề đang học.
- Các dạng bài tập thường gặp: Bài tập áp dụng công thức, bài tập chứng minh, bài tập tìm điều kiện, v.v.
- Ví dụ minh họa: Các bài tập mẫu được giải chi tiết để giúp học sinh hiểu rõ phương pháp giải.
Giải chi tiết các bài tập trang 61, 62, 63
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 1 trang 61, 62, 63 SGK Toán 12 tập 2 Chân trời sáng tạo:
Bài 1: (Trang 61)
(Nội dung bài tập và lời giải chi tiết)
Giải:
(Các bước giải chi tiết, kèm theo giải thích rõ ràng)
Bài 2: (Trang 62)
(Nội dung bài tập và lời giải chi tiết)
Giải:
(Các bước giải chi tiết, kèm theo giải thích rõ ràng)
Bài 3: (Trang 63)
(Nội dung bài tập và lời giải chi tiết)
Giải:
(Các bước giải chi tiết, kèm theo giải thích rõ ràng)
Mẹo giải bài tập hiệu quả
Để giải bài tập Toán 12 tập 2 hiệu quả, các em học sinh nên:
- Nắm vững kiến thức cơ bản: Đọc kỹ SGK, ghi chép đầy đủ các khái niệm, định nghĩa, công thức.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Tìm kiếm sự giúp đỡ khi cần thiết: Hỏi thầy cô, bạn bè hoặc tham khảo các nguồn tài liệu trực tuyến.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm giải toán, v.v.
Tusach.vn – Đồng hành cùng học sinh trên con đường chinh phục Toán học
Tusach.vn cam kết cung cấp cho học sinh những lời giải chính xác, dễ hiểu và đầy đủ nhất. Chúng tôi luôn cập nhật nội dung mới nhất và đa dạng các dạng bài tập để đáp ứng nhu cầu học tập của các em. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chủ đề | Trang | Link |
|---|---|---|
| Giải SGK Toán 12 tập 2 | Tất cả | Tusach.vn |