Giải mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Bài tập trong mục này tập trung vào các kiến thức cơ bản về giới hạn dãy số, một chủ đề quan trọng trong chương trình Toán 12.
Định nghĩa
KP1
Trả lời câu hỏi Khám phá 1 trang 14 SGK Toán 12 Chân trời sáng tạo
Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày.
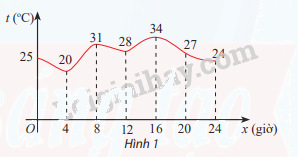
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là \(28^\circ C\).
ii) Nhiệt độ cao nhất trong ngày là \(40^\circ C\).
iii) Nhiệt độ cao nhất trong ngày là \(34^\circ C\).
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
Phương pháp giải:
Quan sát đồ thị hình 1
Lời giải chi tiết:
a) Khẳng định đúng là iii) vì nhìn hình ta thấy điểm cao nhất của đồ thị là \(34^\circ C\)
b) Thời điểm có nhiệt độ cao nhất trong ngày (\(34^\circ C\)) là lúc 16 giờ
c) Nhiệt độ thấp nhất trong ngày là \(20^\circ C\)
VD1
Trả lời câu hỏi Vận dụng1 trang 16 SGK Toán 12 Chân trời sáng tạo
Sử dụng đạo hàm và lập bảng biến thiên, trả lời câu hỏi trong Hoạt động khởi động (trang 14).
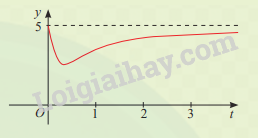
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t \( \ge \) 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)
Phương pháp giải:
Sử dụng đạo hàm và lập bảng biến thiên
Lời giải chi tiết:
Xét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) trên nửa đoạn \([0; + \infty )\)
\(y'(t) = \frac{{135{t^2} - 15}}{{{{(9{t^2} + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{3}\\x = - \frac{1}{3}(loai)\end{array} \right.\)
Bảng biến thiên:
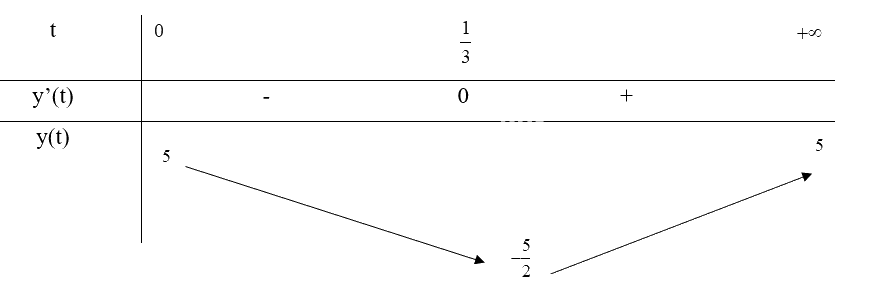
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0; + \infty )} y(t) = y(\frac{1}{3}) = - \frac{5}{2}\) và \(\mathop {\max }\limits_{[0; + \infty )} y(t) = y(0) = 5\)
Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = \(\frac{1}{3}\) giờ thì nồng độ oxygen trong nước thấp nhất
TH1
Trả lời câu hỏi Thực hành 1 trang 16 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
c) \(h(x) = x\sqrt {2 - {x^2}} \)
Phương pháp giải:
Cho hàm số y = f(x) xác định trên tập hợp D.
- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) \( \le \) M với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = M. Kí hiệu M = \(\mathop {\max }\limits_D \)f(x). Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) \( \ge \) m với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = m. Kí hiệu m = \(\mathop {\min }\limits_D \)f(x).
- Tìm đạo hàm f’(x), lập bảng biến thiên và xác định GTLN và GTNN
Lời giải chi tiết:
a) Xét \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
\(f'(x) = 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Bảng biến thiên:
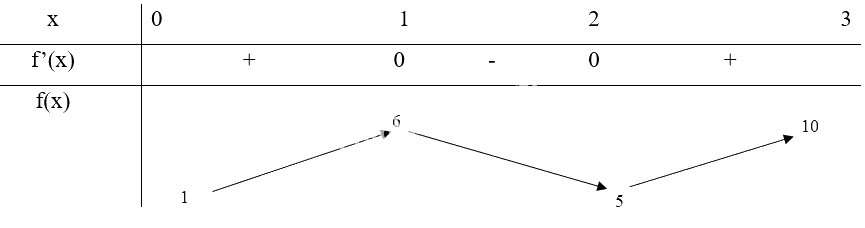
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0;3]} f(x) = f(0) = 1\) và \(\mathop {\max }\limits_{[0;3]} f(x) = f(3) = 10\)
b) Xét \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
\(g'(x) = 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1(loai)\end{array} \right.\)
Bảng biến thiên:
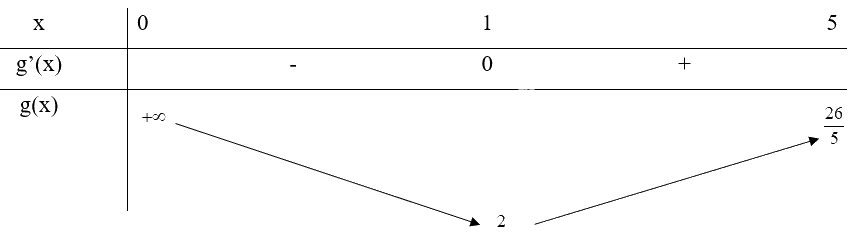
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{(0;5)} f(x) = f(1) = 2\) và hàm số không tồn tại giá trị lớn nhất trên khoảng (0;5)
c) Xét \(h(x) = x\sqrt {2 - {x^2}} \)
Tập xác định: \(D = [ - \sqrt 2 ;\sqrt 2 ]\)
\(h'(x) = \sqrt {2 - {x^2}} - \frac{{{x^2}}}{{\sqrt {2 - {x^2}} }}\)
Tập xác định mới: \({D_1} = ( - \sqrt 2 ;\sqrt 2 )\)
\(h'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
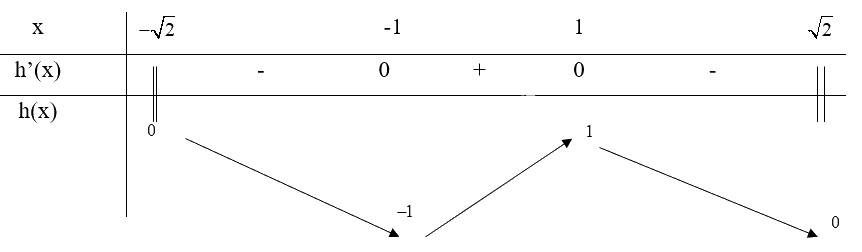
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D f(x) = f( - 1) = - 1\) và \(\mathop {\max }\limits_D f(x) = f(1) = 1\)
- KP1
- TH1
- VD1
Trả lời câu hỏi Khám phá 1 trang 14 SGK Toán 12 Chân trời sáng tạo
Hình 1 cho biết sự thay đổi của nhiệt độ ở một thành phố trong một ngày.
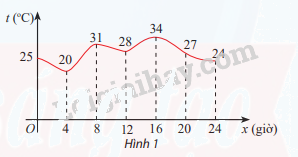
a) Khẳng định nào sau đây đúng? Vì sao?
i) Nhiệt độ cao nhất trong ngày là \(28^\circ C\).
ii) Nhiệt độ cao nhất trong ngày là \(40^\circ C\).
iii) Nhiệt độ cao nhất trong ngày là \(34^\circ C\).
b) Hãy xác định thời điểm có nhiệt độ cao nhất trong ngày.
c) Nhiệt độ thấp nhất trong ngày là bao nhiêu?
Phương pháp giải:
Quan sát đồ thị hình 1
Lời giải chi tiết:
a) Khẳng định đúng là iii) vì nhìn hình ta thấy điểm cao nhất của đồ thị là \(34^\circ C\)
b) Thời điểm có nhiệt độ cao nhất trong ngày (\(34^\circ C\)) là lúc 16 giờ
c) Nhiệt độ thấp nhất trong ngày là \(20^\circ C\)
Trả lời câu hỏi Thực hành 1 trang 16 SGK Toán 12 Chân trời sáng tạo
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
b) \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
c) \(h(x) = x\sqrt {2 - {x^2}} \)
Phương pháp giải:
Cho hàm số y = f(x) xác định trên tập hợp D.
- Số M được gọi là giá trị lớn nhất của hàm số y = f(x) trên D nếu f(x) \( \le \) M với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = M. Kí hiệu M = \(\mathop {\max }\limits_D \)f(x). Số m được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên D nếu f(x) \( \ge \) m với mọi x thuộc D và tồn tại \({x_0}\) thuộc D sao cho f(\({x_0}\)) = m. Kí hiệu m = \(\mathop {\min }\limits_D \)f(x).
- Tìm đạo hàm f’(x), lập bảng biến thiên và xác định GTLN và GTNN
Lời giải chi tiết:
a) Xét \(f(x) = 2{x^3} - 9{x^2} + 12x + 1\) trên đoạn [0;3]
\(f'(x) = 6{x^2} - 18x + 12 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 2\\x = 1\end{array} \right.\)
Bảng biến thiên:
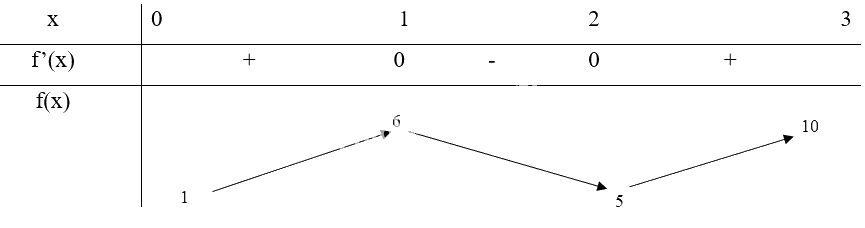
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0;3]} f(x) = f(0) = 1\) và \(\mathop {\max }\limits_{[0;3]} f(x) = f(3) = 10\)
b) Xét \(g(x) = x + \frac{1}{x}\) trên khoảng (0;5)
\(g'(x) = 1 - \frac{1}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1(loai)\end{array} \right.\)
Bảng biến thiên:
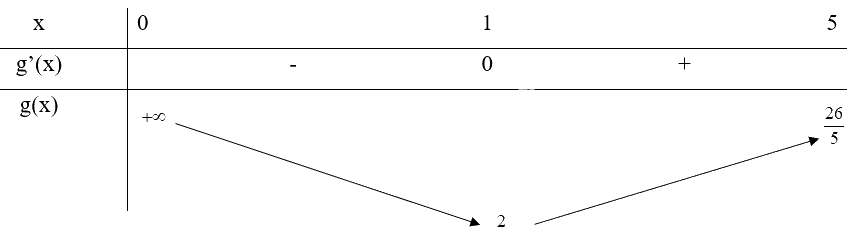
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{(0;5)} f(x) = f(1) = 2\) và hàm số không tồn tại giá trị lớn nhất trên khoảng (0;5)
c) Xét \(h(x) = x\sqrt {2 - {x^2}} \)
Tập xác định: \(D = [ - \sqrt 2 ;\sqrt 2 ]\)
\(h'(x) = \sqrt {2 - {x^2}} - \frac{{{x^2}}}{{\sqrt {2 - {x^2}} }}\)
Tập xác định mới: \({D_1} = ( - \sqrt 2 ;\sqrt 2 )\)
\(h'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\)
Bảng biến thiên:
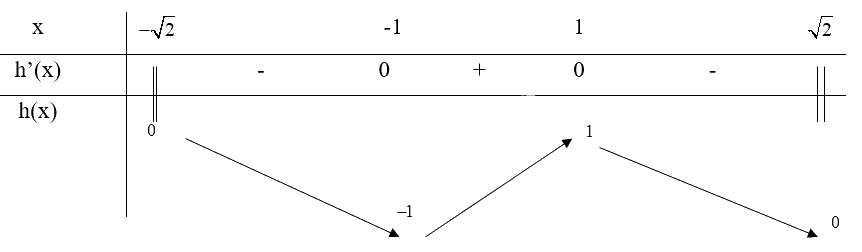
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D f(x) = f( - 1) = - 1\) và \(\mathop {\max }\limits_D f(x) = f(1) = 1\)
Trả lời câu hỏi Vận dụng1 trang 16 SGK Toán 12 Chân trời sáng tạo
Sử dụng đạo hàm và lập bảng biến thiên, trả lời câu hỏi trong Hoạt động khởi động (trang 14).
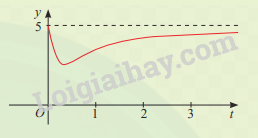
Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau t giờ (t \( \ge \) 0) khi một lượng rác thải hữu cơ bị xả vào hồ được xấp xỉ bởi hàm số (có đồ thị như đường màu đỏ ở hình bên)
\(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\)
Vào các thời điểm nào nồng độ oxygen trong nước cao nhất và thấp nhất?
(Theo: https://www.researchgate.net/publication/264903978_Microrespirometric_ characterization _of_activated_sludge_inhibition_by_copper_and_zinc)
Phương pháp giải:
Sử dụng đạo hàm và lập bảng biến thiên
Lời giải chi tiết:
Xét \(y(t) = 5 - \frac{{15t}}{{9{t^2} + 1}}\) trên nửa đoạn \([0; + \infty )\)
\(y'(t) = \frac{{135{t^2} - 15}}{{{{(9{t^2} + 1)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{1}{3}\\x = - \frac{1}{3}(loai)\end{array} \right.\)
Bảng biến thiên:
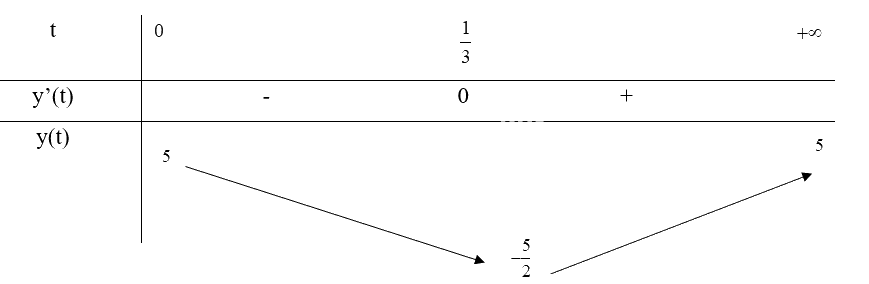
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[0; + \infty )} y(t) = y(\frac{1}{3}) = - \frac{5}{2}\) và \(\mathop {\max }\limits_{[0; + \infty )} y(t) = y(0) = 5\)
Vậy vào các thời điểm t = 0 thì nồng độ oxygen trong nước cao nhất và t = \(\frac{1}{3}\) giờ thì nồng độ oxygen trong nước thấp nhất
Giải mục 1 trang 14, 15, 16 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và hướng dẫn chi tiết
Mục 1 của SGK Toán 12 tập 1 Chân trời sáng tạo giới thiệu về khái niệm giới hạn của dãy số. Đây là nền tảng quan trọng để hiểu các khái niệm nâng cao hơn trong chương trình, như giới hạn hàm số và đạo hàm. Việc nắm vững kiến thức này sẽ giúp các em giải quyết các bài toán liên quan một cách hiệu quả.
Nội dung chính của Mục 1
- Khái niệm dãy số: Định nghĩa dãy số, các loại dãy số (dãy số hữu hạn, dãy số vô hạn, dãy số tăng, dãy số giảm).
- Giới hạn của dãy số: Định nghĩa giới hạn của dãy số, các tính chất của giới hạn.
- Các dạng giới hạn cơ bản: Giới hạn bằng 0, giới hạn bằng một số thực khác 0, giới hạn vô cùng.
- Ứng dụng của giới hạn dãy số: Giải các bài toán liên quan đến giới hạn dãy số, chứng minh sự hội tụ của dãy số.
Hướng dẫn giải chi tiết các bài tập trang 14, 15, 16
Dưới đây là hướng dẫn giải chi tiết các bài tập trong mục 1, trang 14, 15, 16 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 14)
Đề bài: Tìm giới hạn của dãy số un = 2n + 1.
Lời giải:
- Áp dụng định nghĩa giới hạn của dãy số.
- Phân tích biểu thức 2n + 1 khi n tiến tới vô cùng.
- Kết luận: lim un = +∞.
Bài 2: (Trang 15)
Đề bài: Cho dãy số vn = 1/n. Tính lim vn.
Lời giải:
Khi n tiến tới vô cùng, 1/n tiến tới 0. Do đó, lim vn = 0.
Bài 3: (Trang 16)
Đề bài: Chứng minh dãy số wn = (n+1)/n bị chặn.
Lời giải:
Ta có: 1 ≤ wn < 2 với mọi n thuộc N*. Vậy dãy số wn bị chặn.
Mẹo học tốt Toán 12 - Chân trời sáng tạo
- Nắm vững định nghĩa: Hiểu rõ các khái niệm cơ bản về dãy số và giới hạn.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng.
- Sử dụng tài liệu tham khảo: Tham khảo thêm các sách bài tập, đề thi thử để mở rộng kiến thức.
- Hỏi thầy cô giáo: Đừng ngần ngại hỏi thầy cô giáo khi gặp khó khăn.
Tusach.vn - Đồng hành cùng bạn học Toán 12
Tusach.vn là website cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập SGK Toán 12 tập 1 Chân trời sáng tạo. Chúng tôi hy vọng sẽ giúp các em học Toán 12 hiệu quả hơn. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
Chúc các em học tập tốt!