Giải bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn hiểu sâu sắc kiến thức về giới hạn của hàm số.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất.
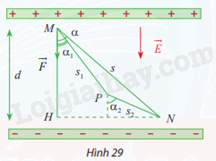
Một lực tĩnh điện \(\overrightarrow F \) tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc MNP (Hình 29). Biết \(q = {2.10^{ - 12}}C\), vectơ điện trường có độ lớn \(E = 1,{8.10^5}\)N/C và d = MH = 5mm. Tính công A sinh bởi lực tĩnh điện \(\overrightarrow F \).
Giải bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức về giới hạn một bên, giới hạn tại vô cùng để giải quyết các bài toán cụ thể. Dưới đây là hướng dẫn chi tiết cách giải bài tập này:
Nội dung bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 8 yêu cầu tính các giới hạn sau:
- limx→2 (x2 - 3x + 2) / (x - 2)
- limx→-1 (x3 + 1) / (x + 1)
- limx→0 sin(5x) / x
- limx→∞ (2x2 + 3x - 1) / (x2 + 2)
Phương pháp giải bài tập về giới hạn
Để giải các bài tập về giới hạn, bạn cần nắm vững các kiến thức sau:
- Khái niệm giới hạn: Hiểu rõ ý nghĩa của giới hạn, giới hạn một bên, giới hạn tại vô cùng.
- Các định lý về giới hạn: Nắm vững các định lý về giới hạn của tổng, hiệu, tích, thương, lũy thừa.
- Các giới hạn đặc biệt: Biết các giới hạn đặc biệt như limx→0 sin(x)/x = 1, limx→0 (1 + x)1/x = e.
- Các phương pháp giải: Sử dụng các phương pháp như phân tích thành nhân tử, chia cả tử và mẫu cho x, sử dụng định lý L'Hopital.
Lời giải chi tiết bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo
1. limx→2 (x2 - 3x + 2) / (x - 2)
Ta có: x2 - 3x + 2 = (x - 1)(x - 2). Do đó:
limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1
2. limx→-1 (x3 + 1) / (x + 1)
Ta có: x3 + 1 = (x + 1)(x2 - x + 1). Do đó:
limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 3
3. limx→0 sin(5x) / x
Đặt t = 5x. Khi x → 0 thì t → 0. Do đó:
limx→0 sin(5x) / x = limt→0 sin(t) / (t/5) = 5 * limt→0 sin(t) / t = 5 * 1 = 5
4. limx→∞ (2x2 + 3x - 1) / (x2 + 2)
Chia cả tử và mẫu cho x2, ta được:
limx→∞ (2x2 + 3x - 1) / (x2 + 2) = limx→∞ (2 + 3/x - 1/x2) / (1 + 2/x2) = (2 + 0 - 0) / (1 + 0) = 2
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem có thể áp dụng trực tiếp các định lý về giới hạn hay không.
- Nếu không, hãy cố gắng biến đổi biểu thức để đưa về dạng có thể áp dụng định lý.
- Chú ý đến các giới hạn đặc biệt.
- Kiểm tra lại kết quả sau khi giải.
Hy vọng với hướng dẫn chi tiết này, bạn đã hiểu rõ cách giải bài tập 8 trang 51 SGK Toán 12 tập 1 - Chân trời sáng tạo. Chúc bạn học tập tốt!
