Lý thuyết Khảo sát và vẽ đồ thị một số hàm số cơ bản Toán 12 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Khảo sát và Vẽ đồ thị hàm số Toán 12 Chân trời sáng tạo
Chương trình Toán 12 Chân trời sáng tạo tập trung vào việc giúp học sinh nắm vững kiến thức về hàm số, đặc biệt là kỹ năng khảo sát và vẽ đồ thị. Đây là một phần quan trọng, thường xuyên xuất hiện trong các kỳ thi THPT Quốc gia.
Bài viết này sẽ cung cấp một cách đầy đủ và dễ hiểu về lý thuyết, các bước thực hiện và ví dụ minh họa để bạn có thể tự tin giải quyết các bài toán liên quan.
1. Sơ đồ khảo sát hàm số Các bước khảo sát hàm số
1. Sơ đồ khảo sát hàm số
Các bước khảo sát hàm số
1. Tìm tập xác định của hàm số 2. Xét sự biến thiên của hàm số
3. Vẽ đồ thị của hàm số
|
2. Khảo sát hàm số \(y = a{x^3} + b{x^2} + cx + d(a \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = - {x^3} + 3{x^2} - 4\)
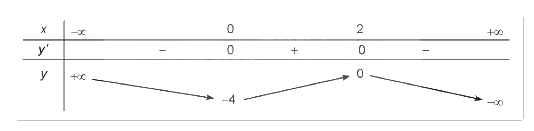
1. Tập xác định của hàm số: R
2. Sự biến thiên:
- Ta có: \(y' = - 3{x^2} + 6x\). Vậy y’ = 0 khi x = 0 hoặc x = 2
- Trên khoảng \(\left( {0;2} \right)\), y’ > 0 nên hàm số đồng biến. Trên các khoảng \(\left( { - \infty ;0} \right)\) và \(\left( {2; + \infty } \right)\), y’ < 0 nên hàm số nghịch biến trên mỗi khoảng đó
- Hàm số đạt cực tiểu tại x = 0, giá trị cực tiểu \({y_{CT}} = - 4\). Hàm số đạt cực đại tại x = 2, giá trị cực đại
- Giới hạn tại vô cực: \(\mathop {\lim }\limits_{x \to - \infty } y = + \infty ;\mathop {\lim }\limits_{x \to + \infty } y = - \infty \)
- BBT:
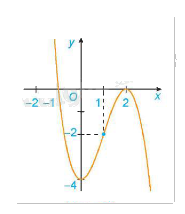
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;4} \right)\)
- Ta có: y = 0 \( \Leftrightarrow \)x = -1 hoặc x = 2. Do đó giao điểm của đồ thị hàm số với trục hoành là các điểm \(\left( { - 1;0} \right)\) và \(\left( {2;0} \right)\)
- Đồ thị hàm số có tâm đối xứng là điểm \(\left( {1; - 2} \right)\
3. Khảo sát hàm số \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{x + 1}}{{x - 2}}\)
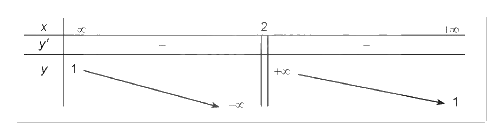
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên:
- Ta có: \(y' = - \frac{3}{{{{(x - 2)}^2}}} < 0\) với mọi \(x \ne 2\)
- Hàm số nghịch biến trên từng khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\)
- Hàm số không có cực trị
- Tiệm cận: \(\mathop {\lim }\limits_{x \to - \infty } y = 1;\mathop {\lim }\limits_{x \to + \infty } - \infty = 1\)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận ngang là y = 1
- BBT:
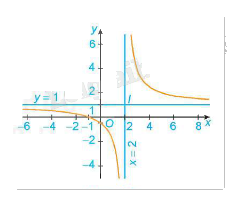
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0; - \frac{1}{2}} \right)\)
- Giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( { - 1;0} \right)\)
- Đồ thị hàm số nhận giao điểm I \(\left( {2;1} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
4. Khảo sát hàm số\(y = \frac{{a{x^2} + bx + c}}{{px + q}}(a \ne 0,p \ne 0)\)(đa thức tử không chia hết cho đa thức mẫu)
Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = \frac{{{x^2} - x - 1}}{{x - 2}}\)
1. Tập xác định của hàm số: R\{2}
2. Sự biến thiên: Viết \(y = x + 1 + \frac{1}{{x - 2}}\)
- Ta có: \(y' = 1 - \frac{1}{{{{(x - 2)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{(x - 2)}^2}}}\) . Vậy y’ = 0 \( \Leftrightarrow \) x = 1 hoặc x = 3
- Trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {3; + \infty } \right)\), y’ > 0 nên hàm số đồng biến trên từng khoảng này
- Trên các khoảng \(\left( {1;2} \right)\) và \(\left( {2;3} \right)\), y’ < 0 nên hàm số nghịch biến trên từng khoảng này
- Hàm số đạt cực đại tại x = 1 với ; hàm số đạt cực tiểu tại x = 3 với \({y_{CT}} = 5\)
- \(\mathop {\lim }\limits_{x \to - \infty } y = - \infty ;\mathop {\lim }\limits_{x \to + \infty } y = + \infty \)
\(\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty ;\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty \)
\(\mathop {\lim }\limits_{x \to + \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{x - 2}} = 0\); \(\mathop {\lim }\limits_{x \to - \infty } \left[ {y - \left( {x + 1} \right)} \right] = \mathop {\lim }\limits_{x \to - \infty } \frac{1}{{x - 2}} = 0\)
Do đó, đồ thị của hàm số có tiệm cận đứng là x = 2, tiệm cận xiên là y = x+1
- BBT:
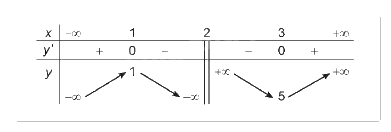
3. Đồ thị:
- Giao điểm của đồ thị hàm số với trục tung là điểm \(\left( {0;\frac{1}{2}} \right)\)
- Ta có: \(y = 0 \Leftrightarrow x = \frac{{1 - \sqrt 5 }}{2};x = \frac{{1 + \sqrt 5 }}{2}\). Do đó giao điểm của đồ thị hàm số với trục hoành là điểm \(\left( {\frac{{1 - \sqrt 5 }}{2};0} \right);\left( {\frac{{1 + \sqrt 5 }}{2};0} \right)\)
- Đồ thị hàm số nhận giao điểm I \(\left( {2;3} \right)\) của hai đường tiệm cận làm tâm đối xứng và nhận hai đường phân giác của các góc tạo bởi hai đường tiệm cận này làm trục đối xứng
5. Vận dụng đạo hàm và khảo sát hàm số để giải quyết một số vấn đề liên quan đến thực tiễn
Ví dụ: Số dân của một thị trấn sau t năm kể từ năm 1970 được ước tính bởi công thức \(f(t) = \frac{{26t + 10}}{{t + 5}}\) (f(t) được tính bằng nghìn người)
a) Tính số dân của thị trấn vào năm 2022
b) Xem y = f(t) là một hàm số xác định trên nửa khoảng \(\left[ {0; + \infty } \right)\). Khảo sát sự biến thiên và vẽ đồ thị của hàm số f(t)
c) Đạo hàm của hàm số y = f(t) biểu thị tốc độ tăng dân số của thị trấn (tính bằng nghìn người/năm)
- Tính tốc độ tăng dân số vào năm 2022 của thị trấn đó
- Vào năm nào thì tốc độ tăng dân số là 0,192 nghìn người/năm ?
Giải:
a) Ta có: \(f(52) = \frac{{26.52 + 10}}{{52 + 5}} = \frac{{1362}}{{57}} \approx 23,895\) (nghìn người)
Vậy số dân của thị trấn vào năm 2022 khoảng 23895 nghìn người
b)
1) Sự biến thiên
- Giới hạn tại vô cực và đường tiệm cận ngang:
\(\mathop {\lim }\limits_{t \to + \infty } f(t) = 26\). Do đó, đường thẳng y = 26 là tiệm cận ngang của đồ thị hàm số.
- BBT:
\(f'(t) = \frac{{120}}{{{{(t + 5)}^2}}} > 0\) với mọi \(t \ge 0\)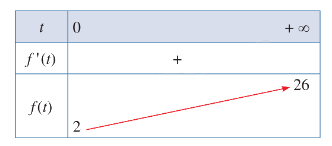
Hàm số đồng biến trên nửa khoảng \(\left[ {0; + \infty } \right)\).
Hàm số không có cực trị
2) Đồ thị
- Giao điểm của đồ thị với trục tung (0;2)
- Đồ thị hàm số đi qua điểm (1;6). Vậy đồ thị hàm số \(y = f(t) = \frac{{26t + 10}}{{t + 5}}\), \(t \ge 0\) được cho ở hình vẽ sau
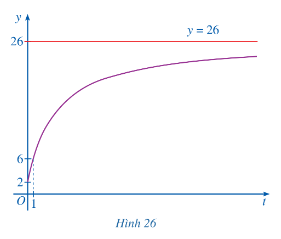
c)
- Tốc độ tăng dân số vào năm 2022 của thị trấn đó là:
\(f'(52) = \frac{{120}}{{{{(52 + 5)}^2}}} = \frac{{40}}{{1083}}\)
- Ta có:
\(f'(t) = 0,192 \Leftrightarrow \frac{{120}}{{{{(t + 5)}^2}}} = 0,192 \Leftrightarrow {(t + 5)^2} = 625 \Leftrightarrow t = 20\) (do \(t \ge 0\))
Vậy vào năm 1990, tốc độ tăng dân số là 0,192 nghìn người/năm.
Lý Thuyết Khảo Sát và Vẽ Đồ Thị Hàm Số Cơ Bản Toán 12 Chân Trời Sáng Tạo
Khảo sát và vẽ đồ thị hàm số là một trong những chủ đề quan trọng bậc nhất trong chương trình Toán 12, đặc biệt là với bộ sách Chân Trời Sáng Tạo. Việc nắm vững lý thuyết và kỹ năng thực hành sẽ giúp học sinh giải quyết hiệu quả các bài toán và đạt kết quả tốt trong các kỳ thi.
1. Tổng Quan về Khảo Sát Hàm Số
Khảo sát hàm số là quá trình nghiên cứu các đặc điểm của hàm số, bao gồm:
- Tập xác định: Tìm tập hợp tất cả các giá trị của x mà hàm số có nghĩa.
- Chiều biến thiên: Xác định hàm số đồng biến, nghịch biến trên các khoảng nào.
- Cực trị: Tìm các điểm cực đại, cực tiểu của hàm số.
- Giới hạn: Tính giới hạn của hàm số tại vô cùng và các điểm gián đoạn.
- Tiệm cận: Xác định các đường tiệm cận đứng, ngang, xiên của đồ thị hàm số.
- Bảng biến thiên: Tổng hợp các thông tin trên vào một bảng để dễ dàng theo dõi.
2. Các Bước Khảo Sát Hàm Số
- Xác định tập xác định của hàm số.
- Tính đạo hàm cấp nhất y'.
- Tìm các điểm tới hạn (y' = 0 hoặc y' không xác định).
- Lập bảng biến thiên của y'.
- Kết luận về chiều biến thiên của hàm số.
- Tính đạo hàm cấp hai y''.
- Tìm các điểm uốn (y'' = 0 và đổi dấu).
- Lập bảng biến thiên của y''.
- Kết luận về tính lồi, lõm của đồ thị hàm số.
- Tính giới hạn của hàm số tại vô cùng và các điểm gián đoạn.
- Tìm tiệm cận (nếu có).
- Vẽ đồ thị hàm số.
3. Khảo Sát Một Số Hàm Số Cơ Bản
a. Hàm số bậc ba: y = ax3 + bx2 + cx + d
Hàm số bậc ba có thể có cực đại, cực tiểu hoặc không có cực trị. Điểm uốn luôn tồn tại và là tâm đối xứng của đồ thị.
b. Hàm số bậc bốn: y = ax4 + bx3 + cx2 + dx + e
Hàm số bậc bốn có thể có cực đại, cực tiểu hoặc không có cực trị. Điểm uốn có thể có hoặc không có.
c. Hàm số mũ: y = ax (a > 0, a ≠ 1)
Hàm số mũ luôn đồng biến hoặc nghịch biến trên tập xác định của nó. Không có cực trị và không có tiệm cận đứng.
d. Hàm số logarit: y = logax (a > 0, a ≠ 1)
Hàm số logarit luôn đồng biến hoặc nghịch biến trên tập xác định của nó. Có tiệm cận đứng x = 0 và không có cực trị.
4. Ví dụ Minh Họa
Ví dụ: Khảo sát hàm số y = x3 - 3x2 + 2
- Tập xác định: R
- Đạo hàm cấp nhất: y' = 3x2 - 6x
- Điểm tới hạn: y' = 0 ⇔ x = 0 hoặc x = 2
- Bảng biến thiên của y': ... (tự vẽ)
- Chiều biến thiên: Hàm số đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2).
- Đạo hàm cấp hai: y'' = 6x - 6
- Điểm uốn: y'' = 0 ⇔ x = 1
- Bảng biến thiên của y'': ... (tự vẽ)
- Tính lồi, lõm: Hàm số lõm trên (-∞; 1) và lồi trên (1; +∞).
- Giới hạn: limx→+∞ y = +∞, limx→-∞ y = -∞
- Tiệm cận: Không có tiệm cận.
- Đồ thị: (Vẽ đồ thị dựa trên các thông tin trên)
5. Lời Khuyên Khi Học và Luyện Tập
- Nắm vững lý thuyết và các công thức đạo hàm.
- Luyện tập thường xuyên với nhiều dạng bài tập khác nhau.
- Sử dụng các công cụ vẽ đồ thị để kiểm tra kết quả.
- Hiểu rõ bản chất của các khái niệm để áp dụng linh hoạt.
Hy vọng bài viết này sẽ giúp bạn hiểu rõ hơn về lý thuyết khảo sát và vẽ đồ thị hàm số Toán 12 Chân Trời Sáng Tạo. Chúc bạn học tập tốt!