Giải mục 2 trang 24,25,26 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 24,25,26 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết và dễ hiểu cho các bài tập trong mục 2 trang 24, 25, 26 sách giáo khoa Toán 12 tập 2 chương trình Chân trời sáng tạo. Chúng tôi luôn cố gắng cung cấp những giải pháp tối ưu, giúp học sinh hiểu rõ bản chất của bài toán và rèn luyện kỹ năng giải quyết vấn đề.
Bài giải được trình bày rõ ràng, logic, kèm theo các lưu ý quan trọng để bạn có thể tự tin làm bài tập và đạt kết quả tốt nhất.
Tính thể tích hình khối
TH5
Trả lời câu hỏi Thực hành 5 trang 25 SGK Toán 12 Chân trời sáng tạo
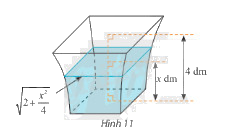
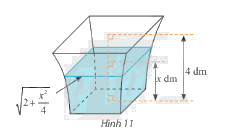
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
Phương pháp giải:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \)
Lời giải chi tiết:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
TH6
Trả lời câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo
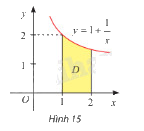
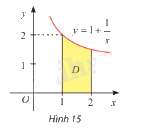
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Phương pháp giải:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)
KP3
Trả lời câu hỏi Khám phá 3 trang 24 SGK Toán 12 Chân trời sáng tạo
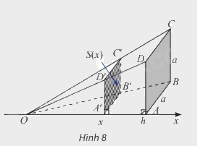
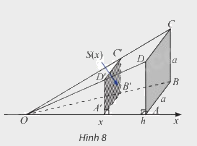
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).
Phương pháp giải:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}}\), từ đó tính được \(A'D'\), sau đó tính \(S\left( x \right)\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau.
Lời giải chi tiết:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
KP4
Trả lời câu hỏi Khám phá 4 trang 25 SGK Toán 12 Chân trời sáng tạo
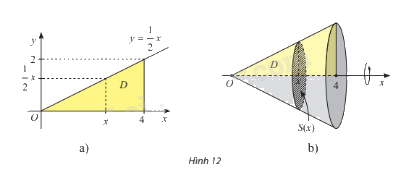
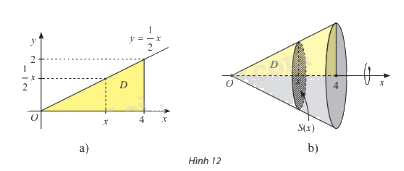
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
Phương pháp giải:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\).
Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\).
b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
VD2
Trả lời câu hỏi Vận dụng 2trang 27 SGK Toán 12 Chân trời sáng tạo
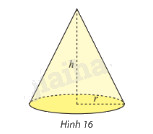
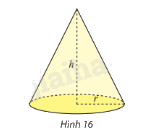
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
Phương pháp giải:
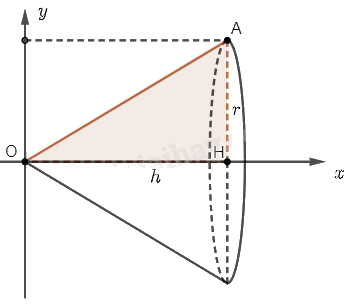
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
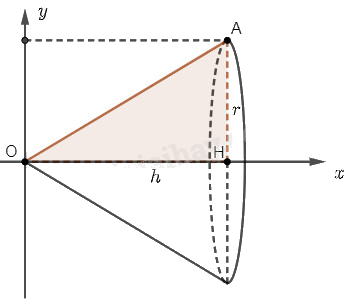
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)
- KP3
- TH5
- KP4
- TH6
- VD2
Trả lời câu hỏi Khám phá 3 trang 24 SGK Toán 12 Chân trời sáng tạo
Trong không gian, cho hình chóp \(O.ABCD\) có đáy là hình vuông cạnh \(a\), \(OA \bot \left( {ABCD} \right)\), \(OA = h\). Đặt trục số \(Ox\) như hình 8. Một mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 < x \le h} \right)\), cắt hình chóp \(O.ABCD\) theo mặt cắt là hình vuông \(A'B'C'D'\). Kí hiệu \(S\left( x \right)\) là diện tích của hình vuông \(A'B'C'D'\).
a) Tính \(S\left( x \right)\) theo \(a\), \(h\) và \(x\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và so sánh với thể tích của khối chóp \(O.ABCD\).
Phương pháp giải:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}}\), từ đó tính được \(A'D'\), sau đó tính \(S\left( x \right)\).
b) Tính \(\int\limits_0^h {S\left( x \right)dx} \) và thể tích khối chóp \(O.ABCD\) và so sánh các kết quả với nhau.
Lời giải chi tiết:
a) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
Trả lời câu hỏi Thực hành 5 trang 25 SGK Toán 12 Chân trời sáng tạo
Một bình chứa nước có dạng như hình 11. Biết rằng khi nước ở trong bình có chiều cao \(x\) (dm) \(\left( {0 \le x \le 4} \right)\) thì mặt nước là hình vuông có cạnh \(\sqrt {2 + \frac{{{x^2}}}{4}} \) (dm). Tính dung tích của bình.
Phương pháp giải:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} \)
Lời giải chi tiết:
Chọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
Trả lời câu hỏi Khám phá 4 trang 25 SGK Toán 12 Chân trời sáng tạo
Cho \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right) = \frac{1}{2}x\), trục hoành và đường thẳng \(x = 4\) (hình 12a). Quay hình \(D\) xung quanh trục \(Ox\) thì được một khối nón, kí hiệu là \(N\). (hình 12b)
a) Cắt khối \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) \(\left( {0 \le x \le 4} \right)\) thì mặt cắt là hình gì? Tính diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Sử dụng công thức tính thể tích hình khối, tính thể tích của khối nón \(N\).
Phương pháp giải:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Tính bán kính của hình tròn, từ đó tính được diện tích \(S\left( x \right)\) của mặt cắt đó.
b) Công thức tính thể tích của khối nón \(N\) có bán kính đáy \(r\) và chiều cao \(h\): \(V = \frac{1}{3}\pi {r^2}h\).
Lời giải chi tiết:
a) Mặt cắt khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) là hình tròn. Ta nhận thấy rằng khi cắt khối nón \(N\) bởi mặt phẳng vuông góc với trục \(Ox\) tại điểm có hoành độ \(x\) thì bán kính mặt cắt sẽ là \(\frac{1}{2}x\).
Do đó diện tích của mặt cắt là \(S\left( x \right) = \pi .{\left( {\frac{1}{2}x} \right)^2} = \frac{\pi }{2}{x^2}\).
b) Khối nón \(N\) có bán kính đáy \(r = 2\) và chiều cao \(h = 4\) nên thể tích của khối nón là: \(V = \frac{1}{3}\pi {.2^2}.4 = \frac{{16\pi }}{3}\)
Trả lời câu hỏi Thực hành 6 trang 26 SGK Toán 12 Chân trời sáng tạo
Gọi \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = 1 + \frac{1}{x}\), trục hoành và hai đường thẳng \(x = 1\), \(x = 2\) (hình 15). Tính thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).
Phương pháp giải:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\), với \(D\) là hình phẳng giới hạn bởi đồ thị hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a\), \(x = b\), là: \(V = \pi \int\limits_a^b {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
Thể tích khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_1^2 {{{\left( {1 + \frac{1}{x}} \right)}^2}dx} = \pi \int\limits_1^2 {\left( {1 + \frac{2}{x} + \frac{1}{{{x^2}}}} \right)dx} = \pi \left. {\left( {x + 2\ln \left| x \right| - \frac{1}{x}} \right)} \right|_1^2 = \pi \left( {\frac{3}{2} + 2\ln 2} \right)\)
Trả lời câu hỏi Vận dụng 2trang 27 SGK Toán 12 Chân trời sáng tạo
Sử dụng tích phân, tính thể tích khối nón có bán kính đáy \(r\) và chiều cao \(h\). (hình 16)
Phương pháp giải:
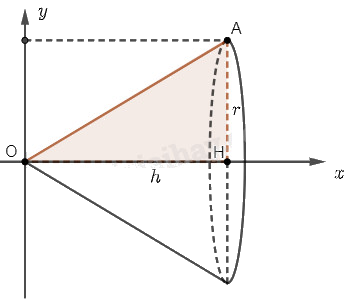
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Thể tích của khối nón là \(V = \pi \int\limits_0^h {{f^2}\left( x \right)dx} \)
Lời giải chi tiết:
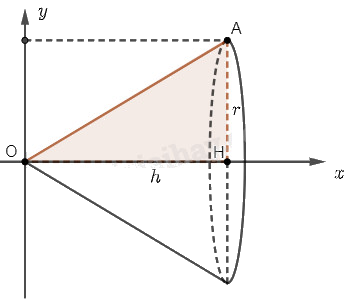
Chọn trục \(Ox\) và \(Oy\) như hình vẽ.
Khi quay hình phẳng \(D\) giới hạn bởi tam giác \(OAH\) quanh trục \(Ox\), ta sẽ được một khối nón có bán kính đáy \(r\) và chiều cao \(h\).
Hình phẳng \(D\) được giới hạn bởi đường thẳng \(OA\) có phương trình \(y = f\left( x \right) = ax + b\), trục hoành và hai đường thẳng \(x = 0\), \(x = h\).
Đường thẳng \(OA\) đi qua điểm \(O\left( {0;0} \right)\) và \(A\left( {h;r} \right)\) nên phương trình đường thẳng \(OA\) là \(y = \frac{r}{h}x\).
Thể tích khối nón là:
\(V = \pi \int\limits_0^h {{{\left( {\frac{r}{h}x} \right)}^2}dx} = \pi \frac{{{r^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{\pi {r^2}}}{{{h^2}}}.\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{\pi {r^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{\pi {r^2}h}}{3}\)
Giải mục 2 trang 24,25,26 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng trong mục này là rất cần thiết để giải quyết các bài toán phức tạp hơn và chuẩn bị cho kỳ thi tốt nghiệp THPT.
Nội dung chính của Mục 2 (trang 24, 25, 26)
Để hiểu rõ hơn về nội dung của mục này, chúng ta cần xem xét các bài tập cụ thể. Thông thường, mục 2 sẽ bao gồm các dạng bài tập sau:
- Dạng 1: Bài tập về lý thuyết, yêu cầu học sinh phát biểu định nghĩa, tính chất, định lý liên quan đến chủ đề.
- Dạng 2: Bài tập áp dụng công thức, tính toán các giá trị cụ thể.
- Dạng 3: Bài tập kết hợp kiến thức, yêu cầu học sinh vận dụng linh hoạt các công thức và định lý để giải quyết vấn đề.
- Dạng 4: Bài tập trắc nghiệm, kiểm tra khả năng hiểu và vận dụng kiến thức của học sinh.
Giải chi tiết từng bài tập
Dưới đây là lời giải chi tiết cho từng bài tập trong mục 2 trang 24, 25, 26 SGK Toán 12 tập 2 - Chân trời sáng tạo:
Bài 1 (Trang 24)
Đề bài: (Ví dụ: Chứng minh rằng hàm số f(x) = x2 + 2x + 1 có giá trị nhỏ nhất tại x = -1)
Lời giải:
- Ta có f(x) = x2 + 2x + 1 = (x + 1)2
- Vì (x + 1)2 ≥ 0 với mọi x, nên f(x) ≥ 0 với mọi x.
- Dấu bằng xảy ra khi x + 1 = 0, tức là x = -1.
- Vậy hàm số f(x) có giá trị nhỏ nhất là 0 tại x = -1.
Bài 2 (Trang 25)
Đề bài: (Ví dụ: Giải phương trình log2(x + 1) = 3)
Lời giải:
log2(x + 1) = 3 ⇔ x + 1 = 23 ⇔ x + 1 = 8 ⇔ x = 7
Bài 3 (Trang 26)
Đề bài: (Ví dụ: Tính tích phân ∫01 x2 dx)
Lời giải:
∫01 x2 dx = [x3/3]01 = (13/3) - (03/3) = 1/3
Lưu ý quan trọng khi giải bài tập
Để giải bài tập Toán 12 hiệu quả, bạn cần lưu ý những điều sau:
- Nắm vững lý thuyết: Hiểu rõ các định nghĩa, tính chất, định lý liên quan đến chủ đề.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Kiểm tra lại kết quả: Sau khi giải xong bài tập, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
- Sử dụng tài liệu tham khảo: Tham khảo các sách giáo khoa, sách bài tập, tài liệu trực tuyến để bổ sung kiến thức và tìm hiểu các phương pháp giải khác nhau.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Hãy truy cập tusach.vn để được hỗ trợ tốt nhất!
| Chủ đề | Trang | Link |
|---|---|---|
| Giải mục 2 | 24, 25, 26 | tusach.vn/giai-toan-12-muc-2 |