Giải bài tập 9 trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 9 trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
Bài tập 9 trang 43 SGK Toán 12 tập 2 thuộc chương trình Toán 12 Chân trời sáng tạo, yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài tập.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 2a\), \(AD = 5a\), \(SA = 3a\). Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right).\)
Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = 2a\), \(AD = 5a\), \(SA = 3a\). Bằng cách thiết lập hệ trục toạ độ \(Oxyz\) như hình dưới đây, tính khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right).\)
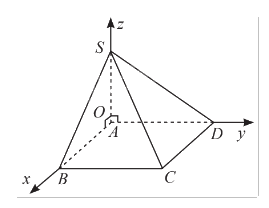
Phương pháp giải - Xem chi tiết
Xác định toạ độ các điểm \(A\), \(S\), \(B\), \(C\). Viết phương trình mặt phẳng \(\left( {SBC} \right)\), từ đó tính được khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right).\)
Lời giải chi tiết
Theo hình vẽ, toạ độ điểm \(A\) là \(A\left( {0;0;0} \right).\)
Điểm \(B\) nằm trên trục \(Ox\), \({x_B} > 0\) và \(AB = 2a\) nên toạ độ điểm \(B\) là \(B\left( {2a;0;0} \right).\)
Điểm \(S\) nằm trên trục \(Oz\), \({z_S} > 0\) và \(SA = 3a\) nên toạ độ điểm \(S\) là \(S\left( {0;0;3a} \right).\)
Điểm \(D\) nằm trên trục \(Oy\), \({y_D} > 0\) và \(AD = 5a\) nên toạ độ điểm \(D\) là \(D\left( {0;5a;0} \right).\)
Điểm \(C\) nằm trên mặt phẳng \(\left( {Oxy} \right)\), \(CB \bot Ox\), \(CD \bot Oy\) nên toạ độ điểm \(C\) là \(C\left( {2a;5a;0} \right).\)
Mặt phẳng \(\left( {SBC} \right)\) đi qua \(S\), \(B\), \(C\). Ta có \(\overrightarrow {SB} = \left( {2a;0; - 3a} \right)\) và \(\overrightarrow {BC} = \left( {0;5a;0} \right)\). Suy ra một cặp vectơ chỉ phương của mặt phẳng \(\left( {SBC} \right)\) là \(\vec u = \frac{1}{a}\overrightarrow {SB} = \left( {2;0; - 3} \right)\) và \(\vec v = \frac{1}{a}\overrightarrow {BC} = \left( {0;5;0} \right).\)
Từ đó, một vectơ pháp tuyến của mặt phẳng \(\left( {SBC} \right)\) là
\(\vec n = \left[ {\vec u,\vec v} \right] = \left( {0.0 - \left( { - 3} \right).5;\left( { - 3} \right).0 - 2.0;2.5 - 0.0} \right) = \left( {15;0;10} \right).\)
Vậy phương trình mặt phẳng \(\left( {SBC} \right)\) là
\(15\left( {x - 0} \right) + 0\left( {y - 0} \right) + 10\left( {z - 3a} \right) = 0 \Leftrightarrow 3x + 2z - 6a = 0.\)
Khoảng cách từ \(A\) đến mặt phẳng \(\left( {SBC} \right)\) là:
\(d\left( {A,\left( {SBC} \right)} \right) = \frac{{\left| {3.0 + 2.0 - 6a} \right|}}{{\sqrt {{3^2} + {2^2}} }} = \frac{{6a\sqrt {13} }}{{13}}.\)
Giải bài tập 9 trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 9 trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo là một bài toán quan trọng trong chương trình học, đòi hỏi học sinh phải nắm vững kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc giải quyết các bài toán thực tế. Dưới đây là hướng dẫn chi tiết cách giải bài tập này, giúp các em học sinh hiểu rõ phương pháp và tự tin làm bài tập.
Đề bài:
Cho hàm số f(x) = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Lời giải:
- Bước 1: Tính đạo hàm f'(x)
- Bước 2: Tìm các điểm làm f'(x) = 0
- Bước 3: Lập bảng xét dấu f'(x)
- Bước 4: Kết luận
- Hàm số f(x) đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.
- Hàm số f(x) đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = -2.
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| f'(x) | + | - | + | |
| f(x) | Đồng biến | Nghịch biến | Đồng biến |
Dựa vào bảng xét dấu, ta thấy:
Lưu ý quan trọng:
Khi giải các bài toán về cực trị của hàm số, cần thực hiện đầy đủ các bước sau:
- Tính đạo hàm cấp một f'(x).
- Tìm các điểm làm f'(x) = 0.
- Lập bảng xét dấu f'(x) để xác định khoảng đồng biến, nghịch biến của hàm số.
- Kết luận về các điểm cực trị và giá trị cực trị.
Mở rộng kiến thức:
Ngoài bài tập 9, các em học sinh có thể tham khảo thêm các bài tập tương tự trong SGK Toán 12 tập 2 - Chân trời sáng tạo để củng cố kiến thức và rèn luyện kỹ năng giải toán. Việc hiểu rõ lý thuyết và thực hành giải nhiều bài tập khác nhau sẽ giúp các em nắm vững kiến thức và đạt kết quả tốt trong các kỳ thi.
Tại sao nên chọn tusach.vn để học Toán 12?
- Lời giải chi tiết, dễ hiểu: Các lời giải được trình bày rõ ràng, logic, giúp các em học sinh dễ dàng theo dõi và nắm bắt kiến thức.
- Đội ngũ giáo viên giàu kinh nghiệm: Các lời giải được biên soạn bởi các giáo viên có nhiều năm kinh nghiệm trong việc giảng dạy Toán 12.
- Cập nhật liên tục: Nội dung được cập nhật thường xuyên, đảm bảo tính chính xác và phù hợp với chương trình học mới nhất.
- Giao diện thân thiện, dễ sử dụng: Website được thiết kế trực quan, dễ dàng tìm kiếm và truy cập thông tin.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin giải bài tập 9 trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo và đạt kết quả tốt trong môn Toán.