Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 7 trang 18 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng về giới hạn của hàm số. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ bản chất bài toán và tự tin giải các bài tập tương tự.
Chúng tôi luôn cập nhật nhanh chóng và chính xác các lời giải bài tập Toán 12, đảm bảo cung cấp cho bạn nguồn tài liệu học tập đáng tin cậy.
Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.
Đề bài
Hộp sữa \(1l\) được thiết kế dạng hình hộp chữ nhật với đáy là hình vuông cạnh x cm. Tìm x để diện tích toàn phần của hộp nhỏ nhất.
Phương pháp giải - Xem chi tiết
Tìm mối liên hệ giữa chiều cao và cạnh đáy, từ đó lập hàm số biểu diễn diện tích toàn phần của hộp theo x. Sau đó tìm đạo hàm, lập bảng biến thiên và xác định giá trị nhỏ nhất
Lời giải chi tiết
Gọi chiều cao của hộp là h (cm)
Thể tích của hộp là: \(V = h.{x^2} = 1 \Leftrightarrow h = \frac{1}{{{x^2}}}\)
Diện tích toàn phần của hộp là: \(y = {S_{tp}} = {S_{xq}} + {S_{day}} = 4hx + 2{x^2} = 4.\frac{1}{{{x^2}}}.x + 2{x^2} = 2{x^2} + \frac{4}{x}\)
Tập xác định: \(D = (0; + \infty )\)
\(y' = 4x - \frac{4}{{{x^2}}} = 0 \Leftrightarrow x = 1\)
Bảng biến thiên:
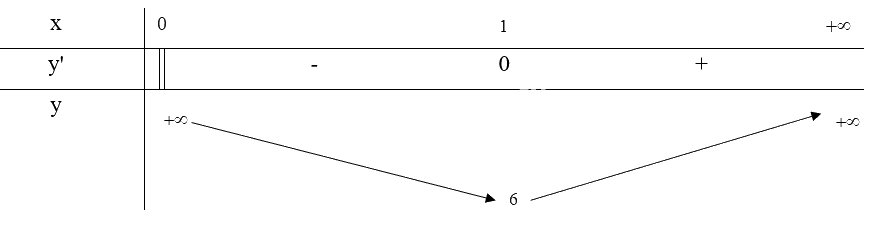
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_D y = y(1) = 6\)
Vậy x = 1cm thì diện tích toàn phần của hộp nhỏ nhất và bằng 6 \(c{m^2}\)
Giải bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết
Bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn của hàm số. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản về giới hạn, các định lý liên quan và các phương pháp tính giới hạn thường gặp.
Nội dung bài tập 7 trang 18 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập yêu cầu tính các giới hạn sau:
- lim (x→2) (x^2 - 3x + 2) / (x - 2)
- lim (x→-1) (x^3 + 1) / (x + 1)
- lim (x→0) (√(x+1) - 1) / x
Hướng dẫn giải chi tiết
1. Giải lim (x→2) (x^2 - 3x + 2) / (x - 2)
Ta có thể phân tích tử thức thành nhân tử:
x^2 - 3x + 2 = (x - 1)(x - 2)
Do đó:
lim (x→2) (x^2 - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
2. Giải lim (x→-1) (x^3 + 1) / (x + 1)
Ta có thể phân tích tử thức thành nhân tử:
x^3 + 1 = (x + 1)(x^2 - x + 1)
Do đó:
lim (x→-1) (x^3 + 1) / (x + 1) = lim (x→-1) (x + 1)(x^2 - x + 1) / (x + 1) = lim (x→-1) (x^2 - x + 1) = (-1)^2 - (-1) + 1 = 1 + 1 + 1 = 3
3. Giải lim (x→0) (√(x+1) - 1) / x
Để tính giới hạn này, ta có thể sử dụng phương pháp nhân liên hợp:
lim (x→0) (√(x+1) - 1) / x = lim (x→0) [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = lim (x→0) (x+1 - 1) / [x(√(x+1) + 1)] = lim (x→0) x / [x(√(x+1) + 1)] = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Lưu ý khi giải bài tập về giới hạn
- Luôn kiểm tra xem có thể rút gọn biểu thức trước khi tính giới hạn hay không.
- Sử dụng các định lý về giới hạn một cách chính xác.
- Khi gặp các dạng giới hạn đặc biệt (ví dụ: 0/0, ∞/∞), cần sử dụng các phương pháp phù hợp (ví dụ: nhân liên hợp, chia đa thức).
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là địa chỉ tin cậy cung cấp lời giải bài tập Toán 12, đáp án nhanh chóng và chính xác. Chúng tôi luôn cập nhật nội dung mới nhất theo chương trình học, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Bài tập | Lời giải |
|---|---|
| Bài tập 7a | 1 |
| Bài tập 7b | 3 |
| Bài tập 7c | 1/2 |