Giải bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 8 trang 86 SGK Toán 12 tập 1 thuộc chương trình học Toán 12 Chân trời sáng tạo, tập trung vào việc rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác và cập nhật nhất để hỗ trợ tối đa cho quá trình học tập của các bạn.
Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B. a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên. b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn? c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
Đề bài
Biểu đồ sau mô tả kết quả điều tra về điểm trung bình năm học của học sinh hai trường A và B.
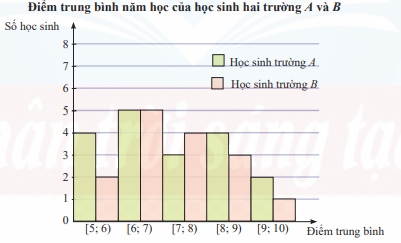 a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên. b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn? c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
a) Hãy xác định giá trị đại diện cho mỗi nhóm và lập bảng tần số ghép nhóm cho mẫu số liệu trên. b) Nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn? c) Nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường nào có điểm trung bình đồng đều hơn?
Phương pháp giải - Xem chi tiết
Khi biểu diễn mẫu số liệu liên tục bởi biểu đồ tần số có dạng cột, các cột thường được vẽ kề nhau. Ta quy ước: cột có đầu mút trái là a và có đầu mút phải là b trên trục hoành biểu diễn cho tần số của nhóm [a; b). Giá trị đại diện của nhóm [a; b) là \(c = \frac{1}{2}(a + b)\)
Khoảng tứ phân vị nhỏ hơn thì số giờ nắng trong tháng 6 của địa phương đó đồng đều hơn
Độ lệch chuẩn nhỏ hơn thì số giờ nắng trong tháng 6 của địa phương đó đồng đều hơn
Lời giải chi tiết
a) 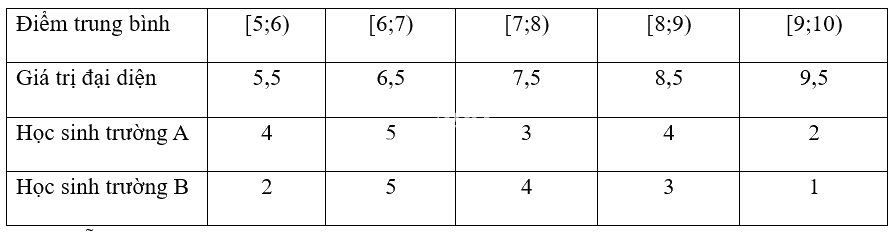
b) Cỡ mẫu: \({n_A} = 18\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{18}}\) là mẫu số liệu gốc về điểm trung bình năm học của học sinh hai trường A được xếp theo thứ tự không giảm.
Ta có: \({x_1};...;{x_4} \in [5;6)\); \({x_5};...;{x_9} \in [6;7)\);\({x_{10}};...;{x_{12}} \in [7;8)\);\({x_{12}}; \ldots ;{\rm{ }}{x_{16}} \in [8;9)\);\({x_{17}};{\rm{ }}{x_{18}} \in [9;10)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_5} \in [6;7)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 6 + \frac{{\frac{{18}}{4} - 4}}{5}(7 - 6) = 6,1\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{14}} \in [8;9)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 8 + \frac{{\frac{{3.18}}{4} - (4 + 5 + 3)}}{4}(9 - 8) = 8,375\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 2,275\)
Cỡ mẫu: \({n_B} = 15\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{15}}\) là mẫu số liệu gốc về điểm trung bình năm học của học sinh hai trường B được xếp theo thứ tự không giảm.
Ta có: \({y_1};{y_2} \in [5;6)\); \({y_3};...;{y_7} \in [6;7)\);\({y_8};...;{y_{11}} \in [7;8)\);\({y_{12}};...;{y_{14}} \in [8;9)\); \({y_{15}} \in [9;10)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_4} \in [6;7)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 6 + \frac{{\frac{{15}}{4} - 2}}{5}(7 - 6) = 6,35\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{12}} \in [8;9)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 8 + \frac{{\frac{{3.15}}{4} - (2 + 5 + 4)}}{3}(9 - 8) = 8,08\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = 1,73\)
Vậy nếu so sánh theo khoảng tứ phân vị của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn
c) Xét số liệu của trường A:
Số trung bình: \(\overline {{x_X}} = \frac{{4.5,5 + 5.6,5 + 3.7,5 + 4.8,5 + 2.9,5}}{{18}} = 7,22\)
Độ lệch chuẩn: \({\sigma _X} = \sqrt {\frac{{4.5,{5^2} + 5.6,{5^2} + 3.7,{5^2} + 4.8,{5^2} + 2.9,{5^2}}}{{18}} - 7,{{22}^2}} \approx 1,79\)
Xét số liệu của trường B:
Số trung bình: \(\overline {{x_Y}} = \frac{{2.5,5 + 5.6,5 + 4.7,5 + 3.8,5 + 1.9,5}}{{15}} = 7,23\)
Độ lệch chuẩn: \({\sigma _Y} = \sqrt {\frac{{2.5,{5^2} + 5.6,{5^2} + 4.7,{5^2} + 3.8,{5^2} + 1.9,{5^2}}}{{15}} - 7,{{23}^2}} \approx 1,31\)
Vậy nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì học sinh trường B có điểm trung bình đồng đều hơn
Giải bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học Toán 12, giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Dưới đây là hướng dẫn giải chi tiết bài tập này, giúp các em học sinh hiểu rõ bản chất bài toán và tự tin làm bài.
Nội dung bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập yêu cầu khảo sát hàm số y = x3 - 3x2 + 2. Cụ thể, học sinh cần thực hiện các bước sau:
- Xác định tập xác định của hàm số.
- Tính đạo hàm bậc nhất y' và tìm các điểm cực trị của hàm số.
- Lập bảng biến thiên của hàm số.
- Vẽ đồ thị hàm số.
Hướng dẫn giải chi tiết
Bước 1: Xác định tập xác định
Hàm số y = x3 - 3x2 + 2 là một hàm đa thức, do đó tập xác định của hàm số là R.
Bước 2: Tính đạo hàm bậc nhất và tìm điểm cực trị
Đạo hàm bậc nhất của hàm số là: y' = 3x2 - 6x.
Để tìm điểm cực trị, ta giải phương trình y' = 0:
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2.
Ta có bảng biến thiên:
| x | -∞ | 0 | 2 | +∞ |
|---|---|---|---|---|
| y' | + | - | + | |
| y | ↗ | ↘ | ↗ |
Từ bảng biến thiên, ta thấy hàm số đạt cực đại tại x = 0, ycđ = 2 và đạt cực tiểu tại x = 2, yct = -2.
Bước 3: Lập bảng biến thiên
Dựa vào kết quả trên, ta có bảng biến thiên của hàm số:
| x | -∞ | 0 | 2 | +∞ | |
|---|---|---|---|---|---|
| y' | + | 0 | - | 0 | + |
| y | -∞ | 2 | -2 | +∞ |
Bước 4: Vẽ đồ thị hàm số
Dựa vào bảng biến thiên, ta có thể vẽ đồ thị hàm số y = x3 - 3x2 + 2.
Lưu ý khi giải bài tập
- Luôn kiểm tra lại các bước tính toán để tránh sai sót.
- Hiểu rõ ý nghĩa của đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số.
- Sử dụng bảng biến thiên để xác định các khoảng đồng biến, nghịch biến, cực đại, cực tiểu của hàm số.
Hy vọng hướng dẫn giải chi tiết bài tập 8 trang 86 SGK Toán 12 tập 1 - Chân trời sáng tạo này sẽ giúp các em học sinh hiểu rõ hơn về bài toán và đạt kết quả tốt trong học tập. Tusach.vn luôn đồng hành cùng các bạn trên con đường chinh phục kiến thức!