Giải bài tập 7 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải Bài Tập 7 Trang 27 Toán 12 Tập 2 - Chân Trời Sáng Tạo
Chào mừng bạn đến với lời giải chi tiết bài tập 7 trang 27 SGK Toán 12 tập 2, chương trình Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp bạn hiểu sâu sắc kiến thức và tự tin làm bài tập.
tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
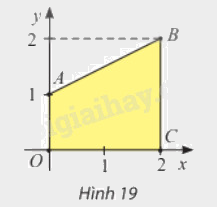
Trong mặt phẳng toạ độ (Oxy), cho hình thang (OABC) có (Aleft( {0;1} right)), (Bleft( {2;2} right)) và (Cleft( {2;0} right)) (hình dưới đây). Tính thể tích khối tròn xoay tạo thành khi quay hình thang (OABC) quanh trục (Ox).
Đề bài
Trong mặt phẳng toạ độ \(Oxy\), cho hình thang \(OABC\) có \(A\left( {0;1} \right)\), \(B\left( {2;2} \right)\) và \(C\left( {2;0} \right)\) (hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang \(OABC\) quanh trục \(Ox\).
Phương pháp giải - Xem chi tiết
Hình thang \(OABC\) được giới hạn bởi các đường thẳng \(AB\), \(OC\) (trục hoành), \(OA\) (trục tung, \(x = 0\)) và \(BC\) \(\left( {x = 2} \right)\). Phương trình đường thẳng \(AB\) là \(y = f\left( x \right) = ax + b\).
Thể tích khối tròn xoay khi quay hình thang \(OABC\) quanh trục \(Ox\) là \(V = \pi \int\limits_0^2 {{f^2}\left( x \right)dx} \).
Lời giải chi tiết
Hình thang \(OABC\) được giới hạn bởi các đường thẳng \(AB\), \(OC\) (trục hoành), \(OA\) (trục tung, \(x = 0\)) và \(BC\) \(\left( {x = 2} \right)\).
Phương trình đường thẳng \(AB\) là \(y = f\left( x \right) = ax + b\). Do \(A\left( {0;1} \right)\), \(B\left( {2;2} \right)\) nên ta có hệ phương trình \(\left\{ {\begin{array}{*{20}{c}}{a.0 + b = 1}\\{a.2 + b = 2}\end{array}} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b = 1\end{array} \right.\)
Vậy phương trình đường thẳng \(AB\) là \(y = \frac{1}{2}x + 1\).
Thể tích khối tròn xoay khi quay hình thang \(OABC\) quanh trục \(Ox\) là:
\(V = \pi \int\limits_0^2 {{{\left( {\frac{1}{2}x + 1} \right)}^2}dx} = \pi \int\limits_0^2 {\left( {\frac{1}{4}{x^2} + x + 1} \right)dx} = \pi \left. {\left( {\frac{{{x^3}}}{{12}} + \frac{{{x^2}}}{2} + x} \right)} \right|_0^2 = \frac{{14}\pi}{3}\).
Giải Bài Tập 7 Trang 27 Toán 12 Tập 2 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết
Bài tập 7 trang 27 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo thuộc chủ đề về đạo hàm của hàm số. Đây là một phần kiến thức quan trọng, nền tảng cho các bài toán ứng dụng đạo hàm trong giai đoạn học tập tiếp theo. Bài viết này sẽ đi sâu vào phân tích từng bước giải bài tập, giúp bạn nắm vững phương pháp và tự tin giải quyết các bài toán tương tự.
Nội Dung Bài Tập 7 Trang 27
Bài tập 7 yêu cầu tính đạo hàm của các hàm số sau:
- a) y = x3 - 3x2 + 2
- b) y = 2x4 + 5x2 - 1
- c) y = -x5 + 4x3 - 7x
- d) y = x2 + 3x + 1/x
Phương Pháp Giải
Để giải bài tập này, chúng ta cần áp dụng các quy tắc tính đạo hàm cơ bản sau:
- Đạo hàm của một tổng/hiệu: (u + v)' = u' + v'
- Đạo hàm của một tích: (uv)' = u'v + uv'
- Đạo hàm của một lũy thừa: (xn)' = nxn-1
- Đạo hàm của một hằng số: (c)' = 0
- Đạo hàm của 1/x: (1/x)' = -1/x2
Lời Giải Chi Tiết
a) y = x3 - 3x2 + 2
y' = (x3)' - 3(x2)' + (2)' = 3x2 - 6x + 0 = 3x2 - 6x
b) y = 2x4 + 5x2 - 1
y' = 2(x4)' + 5(x2)' - (1)' = 8x3 + 10x - 0 = 8x3 + 10x
c) y = -x5 + 4x3 - 7x
y' = -(x5)' + 4(x3)' - 7(x)' = -5x4 + 12x2 - 7
d) y = x2 + 3x + 1/x
y' = (x2)' + 3(x)' + (1/x)' = 2x + 3 - 1/x2
Lưu Ý Quan Trọng
Khi tính đạo hàm, cần chú ý đến các quy tắc và áp dụng chính xác. Đặc biệt, đối với các hàm số phức tạp, nên phân tích thành các thành phần đơn giản trước khi tính đạo hàm.
Bài Tập Tương Tự
Để củng cố kiến thức, bạn có thể thử giải các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = 4x3 - 2x2 + x - 5
- Tính đạo hàm của hàm số y = x4 - 3x2 + 2x + 1
Kết Luận
Hy vọng với lời giải chi tiết và phương pháp giải rõ ràng trên, bạn đã hiểu rõ cách giải bài tập 7 trang 27 SGK Toán 12 tập 2 chương trình Chân trời sáng tạo. Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong các kỳ thi.
Nếu bạn có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với tusach.vn để được hỗ trợ.