Giải mục 3 trang 60,61,62 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải Mục 3 Trang 60, 61, 62 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo
Chào mừng các em học sinh đến với lời giải chi tiết Mục 3 trang 60, 61, 62 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Vận dụng
TH3
Trả lời câu hỏi Thực hành 3 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).
a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)
b) Tính các độ dài MN, NP, MP.
Phương pháp giải:
a) Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết:
a) \(\overrightarrow {MN} = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)
\(\overrightarrow {NP} = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)
\(\overrightarrow {MP} = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)
b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}} = 2\sqrt {69} \)
\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}} = \sqrt {118} \)
\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}} = 3\sqrt {10} \)
KP3
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)
KP4
Trả lời câu hỏi Khám phá 4 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OB} = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)
\(\overrightarrow {OM} = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)
\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)
TH4
Trả lời câu hỏi Thực hành 4 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.
Phương pháp giải:
Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)
\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).
\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)
b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)
TH5
Trả lời câu hỏi Thực hành 5 trang 63 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M
Phương pháp giải:
a)\(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
VD4
Trả lời câu hỏi Vận dụng 4 trang 64 SGK Toán 12 Chân trời sáng tạo
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)
Phương pháp giải:
a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
- KP3
- TH3
- KP4
- TH4
- VD3
- TH5
- VD4
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Trả lời câu hỏi Khám phá 3 trang 60 SGK Toán 12 Chân trời sáng tạo
Cho hai điểm \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B})\). Từ biểu thức \(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} \), tìm toạ độ của vectơ \(\overrightarrow {AB} \) theo toạ độ hai điểm A, B.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {AB} = \overrightarrow {OB} - \overrightarrow {OA} = ({x_A};{y_A};{z_A}) - ({x_B};{y_B};{z_B}) = ({x_A} - {x_B};{y_A} - {y_B};{z_A} - {z_B})\)
Trả lời câu hỏi Thực hành 3 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho ba điểm M(7; –2; 0), N(–9; 0; 4), P(0; –6; 5).
a) Tìm toạ độ của các vectơ \(\overrightarrow {MN} ,\overrightarrow {NP} ,\overrightarrow {MP} \)
b) Tính các độ dài MN, NP, MP.
Phương pháp giải:
a) Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a - \overrightarrow b = ({a_1} - {b_1};{a_2} - {b_2};{a_3} - {b_3})\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
Lời giải chi tiết:
a) \(\overrightarrow {MN} = ( - 9 - 7;0 - ( - 2);4 - 0) = ( - 16;2;4)\)
\(\overrightarrow {NP} = (0 - ( - 9); - 6 - 0;5 - 4) = (9; - 6;1)\)
\(\overrightarrow {MP} = (0 - 7; - 6 - ( - 2);5 - 0) = ( - 7; - 4;5)\)
b) \(MN = \sqrt {{{( - 16)}^2} + {2^2} + {4^2}} = 2\sqrt {69} \)
\(NP = \sqrt {{9^2} + {{( - 6)}^2} + {1^2}} = \sqrt {118} \)
\(MP = \sqrt {{{( - 7)}^2} + {{( - 4)}^2} + {5^2}} = 3\sqrt {10} \)
Trả lời câu hỏi Khám phá 4 trang 61 SGK Toán 12 Chân trời sáng tạo
Cho tam giác ABC có \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Gọi \(M({x_M};{y_M};{z_M})\) là trung điểm của đoạn thẳng AB và \(G({x_G};{y_G};{z_G})\) là trọng tâm của tam giác ABC. Sử dụng các hệ thức vectơ \(\overrightarrow {OM} = \frac{1}{2}(\overrightarrow {OA} + \overrightarrow {OB} )\),\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} )\), tìm toạ độ của các điểm M và G.
Phương pháp giải:
Cho hai vectơ \(\overrightarrow a = ({a_1};{a_2};{a_3})\), \(\overrightarrow b = ({b_1};{b_2};{b_3})\), ta có \(\overrightarrow a + \overrightarrow b = ({a_1} + {b_1};{a_2} + {b_2};{a_3} + {b_3})\)
Lời giải chi tiết:
\(\overrightarrow {OA} + \overrightarrow {OB} = ({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B})\)
\(\overrightarrow {OM} = \frac{1}{2}({x_A} + {x_B};{y_A} + {y_B};{z_A} + {z_B}) = (\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)=> \(M(\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2})\)
\(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} = {x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}\)
\(\overrightarrow {OG} = \frac{1}{3}(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} ) = \frac{1}{3}({x_A} + {x_B} + {x_C};{y_A} + {y_B} + {y_C};{z_A} + {z_B} + {z_C}) = (\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)=> \(G(\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3})\)
Trả lời câu hỏi Thực hành 4 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(2; 1; 3), N(1; 2; 3), P(–3; –1; 0). Tìm toạ độ:
a) Các điểm M′, N′, P′ lần lượt là trung điểm của các cạnh NP, MP, MN;
b) Trọng tâm G của tam giác M′N′P′.
Phương pháp giải:
Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(M'(\frac{{1 - 3}}{2};\frac{{2 - 1}}{2};\frac{3}{2})\) hay \(M'( - 1;\frac{1}{2};\frac{3}{2})\)
\(N'(\frac{{2 - 3}}{2};\frac{{1 - 1}}{2};\frac{3}{2})\) hay \(N'( - \frac{1}{2};0;\frac{3}{2})\).
\(P'(\frac{{2 + 1}}{2};\frac{{1 + 2}}{2};\frac{{3 + 3}}{2})\) hay \(P'(\frac{3}{2};\frac{3}{2};3)\)
b) \(G(\frac{{2 + 1 - 3}}{3};\frac{{1 + 2 - 1}}{3};\frac{{3 + 3 + 0}}{3})\) hay \(G(0;\frac{2}{3};1)\)
Trả lời câu hỏi Vận dụng 3 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC
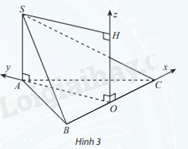
Phương pháp giải:
\(\overrightarrow {OA} = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
Trả lời câu hỏi Thực hành 5 trang 63 SGK Toán 12 Chân trời sáng tạo
Cho tam giác MNP có M(0; 1; 2), N(5; 9; 3), P(7; 8; 2).
a) Tìm toạ độ điểm K là chân đường cao kẻ từ M của tam giác MNP.
b) Tìm độ dài cạnh MN và MP.
c) Tính góc M
Phương pháp giải:
a)\(\overrightarrow a \bot \overrightarrow b \Rightarrow \overrightarrow a .\overrightarrow b = 0\)
b) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
c) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) Ta có: \(\overrightarrow {NP} = (2; - 1; - 1)\)
Gọi K(x;y;z) là chân đường cao kẻ từ M của tam giác MNP
=> \(\overrightarrow {NK} = (x - 5;y - 9;z - 3)\)
\(\overrightarrow {NK} \) cùng phương với \(\overrightarrow {NP} \) nên \(x - 5 = 2t;y - 9 = - t;z - 3 = - t\) => \(K(2t + 2; - t + 9; - t + 3)\)
Ta có: \(\overrightarrow {MK} = (2t + 2; - t + 8; - t + 1)\)
\(\overrightarrow {MK} \bot \overrightarrow {NP} \Leftrightarrow \overrightarrow {MK} .\overrightarrow {NP} = 0 \Leftrightarrow (2t + 2).2 - ( - t + 8) - ( - t + 1) = 0 \Leftrightarrow t = \frac{5}{6}\)
Vậy \(K(\frac{{11}}{3};\frac{{49}}{6};\frac{{13}}{6})\)
b) Ta có: \(\overrightarrow {MN} = (5;8;1) \Rightarrow MN = \sqrt {{5^2} + {8^2} + {1^2}} = 3\sqrt {10} \)
\(\overrightarrow {MP} = (7;7;0) \Rightarrow MP = \sqrt {{7^2} + {7^2}} = 7\sqrt 2 \)
c) \(\cos M = \frac{{\overrightarrow {MN} .\overrightarrow {MP} }}{{|\overrightarrow {MN} |.|\overrightarrow {MP} |}} = \frac{{5.7 + 8.7}}{{3\sqrt {10} .7\sqrt 2 }} = \frac{{13\sqrt 5 }}{{30}}\)
Trả lời câu hỏi Vận dụng 4 trang 64 SGK Toán 12 Chân trời sáng tạo
Trên phần mềm mô phỏng việc điều khiển drone giao hàng trong không gian Oxyz, một đội gồm ba drone giao hàng A, B, C đang có toạ độ là A(1; 1; 1), B(5; 7; 9), C(9; 11 ; 4). Tính:
a) Các khoảng cách giữa mỗi cặp drone giao hàng.
b) Góc \(\widehat {BAC}\)
Phương pháp giải:
a) Công thức tính độ lớn vecto: \(|\overrightarrow a | = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} \)
b) \(\cos (\overrightarrow a ,\overrightarrow b ) = \frac{{\overrightarrow a .\overrightarrow b }}{{|\overrightarrow a |.|\overrightarrow b |}}\)
Lời giải chi tiết:
a) \(\overrightarrow {AB} = (4;6;8) \Rightarrow AB = \sqrt {{4^2} + {6^2} + {8^2}} = 2\sqrt {29} \)
\(\overrightarrow {AC} = (8;10;3) \Rightarrow \sqrt {{8^2} + {{10}^2} + {3^2}} = \sqrt {173} \)
\(\overrightarrow {BC} = (4;4; - 5) \Rightarrow \sqrt {{4^2} + {4^2} + {{( - 5)}^2}} = \sqrt {57} \)
c) \(\cos \widehat {BAC} = \frac{{\overrightarrow {AB} .\overrightarrow {AC} }}{{|\overrightarrow {AB} |.|\overrightarrow {AC} |}} = \frac{{4.8 + 6.10 + 8.3}}{{2\sqrt {29} .\sqrt {173} }} \approx 0,82 \Rightarrow \widehat {BAC} = 35,03^\circ \)
VD3
Trả lời câu hỏi Vận dụng 3 trang 62 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp S.ABC có \(SA \bot (ABC)\), SA = a và đáy ABC là tam giác đều cạnh a, O là trung điểm của BC. Bằng cách thiết lập hệ toạ độ như hình vẽ, hãy tìm toạ độ:
a) Các điểm A, S, B, C
b) Trung điểm M của SB và trung điểm N của SC;
c) Trọng tâm G của tam giác SBC
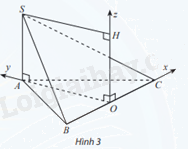
Phương pháp giải:
\(\overrightarrow {OA} = (a;b;c) \Rightarrow A(a;b;c)\). Cho tam giác ABC có \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\), \(C({c_1};{c_2};{c_3})\), ta có \(M(\frac{{{a_1} + {b_1}}}{2};\frac{{{a_2} + {b_2}}}{2};\frac{{{a_3} + {b_3}}}{2})\) là trung điểm của AB, \(G(\frac{{{a_1} + {b_1} + {c_1}}}{3};\frac{{{a_2} + {b_2} + {c_2}}}{3};\frac{{{a_3} + {b_3} + {c_3}}}{3})\) là trọng tâm của tam giác ABC
Lời giải chi tiết:
a) \(OA = \sqrt {A{B^2} - O{B^2}} = \sqrt {{a^2} - {{(\frac{a}{2})}^2}} = \frac{{a\sqrt 3 }}{2}\)
\(\overrightarrow {OA} = \frac{{a\sqrt 3 }}{2}\overrightarrow j = (0;\frac{{a\sqrt 3 }}{2};0) \Rightarrow A(0;\frac{{a\sqrt 3 }}{2};0)\)
\(\overrightarrow {OB} = - \frac{a}{2}\overrightarrow i = ( - \frac{a}{2};0;0) \Rightarrow B( - \frac{a}{2};0;0)\)
\(\overrightarrow {OC} = \frac{a}{2}\overrightarrow i = (\frac{a}{2};0;0) \Rightarrow C(\frac{a}{2};0;0)\)
\(\overrightarrow {OS} = \frac{{a\sqrt 3 }}{2}\overrightarrow j + a\overrightarrow k = (0;\frac{{a\sqrt 3 }}{2};a) \Rightarrow S(0;\frac{{a\sqrt 3 }}{2};a)\)
b) \(M(\frac{{0 - \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(M( - \frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
\(N(\frac{{0 + \frac{a}{2}}}{2};\frac{{\frac{{a\sqrt 3 }}{2}}}{2};\frac{a}{2})\) hay \(N(\frac{a}{2};\frac{{a\sqrt 3 }}{4};\frac{a}{2})\)
c) \(G(\frac{{0 + \frac{a}{2} - \frac{a}{2}}}{3};\frac{{\frac{{a\sqrt 3 }}{2}}}{3};\frac{a}{3})\) hay \(G(0;\frac{{a\sqrt 3 }}{6};\frac{a}{3})\)
Giải Mục 3 Trang 60, 61, 62 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo: Tổng Quan và Phương Pháp Giải
Mục 3 trong SGK Toán 12 tập 1 chương trình Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể, đòi hỏi học sinh phải nắm vững lý thuyết và kỹ năng giải toán liên quan. Việc giải các bài tập trong mục này không chỉ giúp các em củng cố kiến thức mà còn rèn luyện tư duy logic và khả năng vận dụng kiến thức vào thực tế.
Nội Dung Chính của Mục 3
Thông thường, Mục 3 sẽ xoay quanh các chủ đề như:
- Đạo hàm của hàm số lượng giác: Tính đạo hàm của các hàm số sin, cos, tan, cot và các hàm hợp.
- Ứng dụng đạo hàm để khảo sát hàm số: Xác định khoảng đồng biến, nghịch biến, cực trị và vẽ đồ thị hàm số.
- Bài toán tối ưu: Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng cho trước.
Phương Pháp Giải Bài Tập Hiệu Quả
Để giải tốt các bài tập trong Mục 3, các em cần:
- Nắm vững lý thuyết: Hiểu rõ các công thức đạo hàm, quy tắc tính đạo hàm và các khái niệm liên quan.
- Phân tích đề bài: Xác định rõ yêu cầu của đề bài, các điều kiện ràng buộc và các thông tin quan trọng.
- Lựa chọn phương pháp giải phù hợp: Tùy thuộc vào từng bài toán cụ thể, các em có thể sử dụng các phương pháp như đạo hàm, khảo sát hàm số, phương pháp đổi biến số, hoặc phương pháp đánh giá.
- Kiểm tra lại kết quả: Sau khi giải xong bài toán, các em nên kiểm tra lại kết quả để đảm bảo tính chính xác.
Giải Chi Tiết Các Bài Tập Trang 60, 61, 62
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 3 trang 60, 61, 62 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 60)
Đề bài: Tính đạo hàm của hàm số f(x) = 2sin(x) + 3cos(x).
Lời giải:
f'(x) = 2cos(x) - 3sin(x)
Bài 2: (Trang 61)
Đề bài: Tìm khoảng đồng biến của hàm số y = x3 - 3x2 + 2.
Lời giải:
y' = 3x2 - 6x. Giải phương trình y' = 0, ta được x = 0 hoặc x = 2. Khảo sát dấu của y' trên các khoảng (-∞; 0), (0; 2), (2; +∞), ta thấy hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
Bài 3: (Trang 62)
Đề bài: Tìm giá trị lớn nhất của hàm số y = -x2 + 4x - 1 trên đoạn [0; 3].
Lời giải:
y' = -2x + 4. Giải phương trình y' = 0, ta được x = 2. Tính giá trị của hàm số tại các điểm x = 0, x = 2, x = 3, ta được y(0) = -1, y(2) = 3, y(3) = 2. Vậy giá trị lớn nhất của hàm số trên đoạn [0; 3] là 3.
Lưu Ý Quan Trọng
Trong quá trình giải toán, các em cần chú ý:
- Sử dụng đúng các công thức đạo hàm và quy tắc tính đạo hàm.
- Kiểm tra kỹ các điều kiện ràng buộc của bài toán.
- Biết cách trình bày lời giải một cách rõ ràng, logic và dễ hiểu.
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn trong việc giải các bài tập trong Mục 3 trang 60, 61, 62 SGK Toán 12 tập 1 Chân trời sáng tạo. Chúc các em học tập tốt!