Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Khoảng tứ phân vị
VD
Trả lời câu hỏi Vận dụng trang 73 SGK Toán 12 Chân trời sáng tạo
Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của từng mẫu số liệu ghép nhóm ứng với mỗi khu vực A và B.
b) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực nào có độ tuổi kết hôn đồng đều hơn?
Phương pháp giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Khoảng tứ phân vị càng bé thì dữ liệu càng tập trung xung quanh trung vị
Lời giải chi tiết:
Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: 34 – 19 = 15(tuổi)
Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: 31 – 19 = 12(tuổi)
Cỡ mẫu \(n = 100\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực A được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{10}} \in [19;22)\); \({x_{11}}; \ldots ;{\rm{ }}{x_{37}} \in [22;25)\);\({x_{38}}; \ldots ;{\rm{ }}{x_{68}} \in [25;28)\);\({x_{69}}; \ldots ;{\rm{ }}{x_{93}} \in [28;31)\);\({x_{94}}; \ldots ;{\rm{ }}{x_{100}} \in [31;34)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [22;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 22 + \frac{{\frac{{100}}{4} - 10}}{{27}}(25 - 22) = \frac{{71}}{3}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [28;31)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 28 + \frac{{\frac{{3.100}}{4} - (10 + 27 + 31)}}{{25}}(31 - 28) = \frac{{721}}{{25}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{388}}{{75}}\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực B được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{47}} \in [19;22)\); \({y_{48}}; \ldots ;{\rm{ }}{y_{87}} \in [22;25)\);\({y_{88}}; \ldots ;{\rm{ }}{y_{98}} \in [25;30)\);\({y_{99}};{y_{100}} \in [28;31)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_{25}} + {y_{26}}) \in [19;22)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 19 + \frac{{\frac{{100}}{4}}}{{47}}(22 - 19) = \frac{{968}}{{47}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({y_{75}} + {y_{76}}) \in [22;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 22 + \frac{{\frac{{3.100}}{4} - 47}}{{40}}(25 - 22) = \frac{{241}}{{10}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{1647}}{{470}}\)
b) Có \({\Delta _Q}' < {\Delta _Q}\) nên phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn
TH3
Trả lời câu hỏi Thực hành 3 trang 73 SGK Toán 12 Chân trời sáng tạo
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

b) Hãy so sánh độ phân tán của nửa giữa hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở Thực hành 1.

Phương pháp giải:
a) Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Tìm khoảng tứ phân vị của 2 nhóm số liệu rồi so sánh
Lời giải chi tiết:
a) Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm.
Khoảng biến thiên R = 33 – 15 = 18 (phút).
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{22}} \in [15;18)\); \({x_{23}}; \ldots ;{\rm{ }}{x_{60}} \in [18;21)\); \({x_{61}}; \ldots ;{\rm{ }}{x_{87}} \in [21;24)\); \({x_{88}}; \ldots ;{\rm{ }}{x_{95}} \in [24;27)\);\({x_{96}}; \ldots ;{\rm{ }}{x_{99}} \in [27;30)\);\({x_{100}} \in [30;33)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 18 + \frac{{\frac{{100}}{4} - 22}}{{38}}(21 - 18) = \frac{{693}}{{38}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 21 + \frac{{\frac{{3.100}}{4} - (22 + 38)}}{{27}}(24 - 21) = \frac{{68}}{3}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{505}}{{114}}\).
Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\).
Hay \(x > \frac{{68}}{3} + 1,5.\frac{{505}}{{114}} = 29,31\) hoặc \(x < \frac{{693}}{{38}} - 1,5.\frac{{505}}{{114}} = 11,59\).
Do đó, chỉ có đúng 1 lần ông Thắng đi hết 32 phút là giá trị ngoại lệ của mẫu số liệu ghép nhóm.
Khoảng biến thiên của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ: 30 – 15 = 15 (phút).
Gọi \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{99}}\) là mẫu số liệu gốc gồm thời gian 99 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm, sau khi đã loại bỏ giá trị ngoại lệ.
Ta có: \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{22}} \in [15;18)\); \({z_{23}}; \ldots ;{\rm{ }}{z_{60}} \in [18;21); {z_{61}}; \ldots ;{\rm{ }}{z_{87}} \in [21;24); {z_{88}}; \ldots ;{\rm{ }}{z_{95}} \in [24;27); {z_{95}}; \ldots ;{\rm{ }}{z_{99}} \in [27;30) \).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}'' = 18 + \frac{{\frac{{99}}{4}}-22}{{38}}(21 - 18) = \frac{{2769}}{{152}}\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}'' = 21 + \frac{{\frac{{3.99}}{4} - (22+38)}}{{27}}(24 - 21) = \frac{{271}}{{12}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}'' = {Q_3}'' - {Q_1}'' = \frac{{1991}}{{456}}\).
Nhận xét: Sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên mới giảm mạnh còn khoảng tứ phân vị mới không bị ảnh hưởng nhiều.
b) Cỡ mẫu \(n = 25\).
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2} \in [155;160)\); \({x_3}; \ldots ;{\rm{ }}{x_9} \in [160;165)\);\({x_{10}}; \ldots ;{\rm{ }}{x_{21}} \in [165;170)\);\({x_{22}}; \ldots ;{\rm{ }}{x_{24}} \in [170;175)\);\({x_{25}} \in [180;185)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_6} + {x_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 160 + \frac{{\frac{{25}}{4} - 2}}{7}(165 - 160) = \frac{{4565}}{{28}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 165 + \frac{{\frac{{3.25}}{4} - (2 + 7)}}{{12}}(170 - 165) = \frac{{2705}}{{16}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{675}}{{112}}\).
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [155;160)\); \({y_6}; \ldots ;{\rm{ }}{y_{14}} \in [160;165)\);\({y_{15}}; \ldots ;{\rm{ }}{y_{22}} \in [165;170)\);\({y_{23}};{\rm{ }}{{\rm{y}}_{24}} \in [170;175)\);\({y_{25}} \in [175;180)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_6} + {y_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 160 + \frac{{\frac{{25}}{4} - 5}}{9}(165 - 160) = \frac{{5785}}{{36}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 165 + \frac{{\frac{{3.25}}{4} - (5 + 9)}}{8}(170 - 165) = \frac{{5375}}{{32}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{2095}}{{288}}\).
Có \({\Delta _Q}' > {\Delta _Q}\) nên chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lơn hơn lớp 12C.
KP2
Trả lời câu hỏi Khám phá 2 trang 70 SGK Toán 12 Chân trời sáng tạo
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:

a) Hãy tìm các tứ phân vị \({Q_1}\) và \({Q_3}\).
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?
Phương pháp giải:
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Lời giải chi tiết:
a) Cỡ mẫu n = 150
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{150}}\) là mẫu số liệu gốc gồm thu nhập của 150 hộ gia đình được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{24}} \in [200;250)\); \({x_{25}}; \ldots ;{\rm{ }}{x_{86}} \in [250;300)\); \({x_{87}}; \ldots ;{\rm{ }}{x_{120}} \in [300;350)\); \({x_{121}}; \ldots ;{\rm{ }}{x_{141}} \in [350;400)\); \({x_{142}}; \ldots ;{\rm{ }}{x_{150}} \in [400;450)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{38}} \in [250;300)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 250 + \frac{{\frac{{150}}{4} - 24}}{{62}}(300 - 250) = \frac{{16175}}{{62}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{113}} \in [300;350)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 300 + \frac{{\frac{{3.150}}{4} - (24 + 62)}}{{34}}(350 - 300) = \frac{{11525}}{{34}}\)
b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng \([{Q_1};{Q_3}) = [260,89;338,97)\)(triệu đồng)
TH2
Trả lời câu hỏi Thực hành 2 trang 71 SGK Toán 12 Chân trời sáng tạo
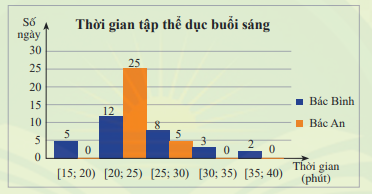
Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Khởi động.

Phương pháp giải:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết:
Cỡ mẫu \(n = 30\);
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}} \in [20;25)\); \({x_{26}}; \ldots ;{\rm{ }}{x_{30}} \in [25;30)\);
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 20 + \frac{{\frac{{30}}{4}}}{{25}}(25 - 20) = \frac{{43}}{2}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in [20;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 20 + \frac{{\frac{{3.30}}{4}}}{{25}}(25 - 20) = \frac{{49}}{2}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 3\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [15;20)\); \({y_6}; \ldots ;{\rm{ }}{y_{17}} \in [20;25)\);\({y_{18}}; \ldots ;{\rm{ }}{y_{25}} \in [25;30)\);\({y_{26}};{y_{27}};{\rm{ }}{y_{28}} \in [30;35)\);\({y_{29}};{y_{30}} \in [35;40)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 20 + \frac{{\frac{{30}}{4}}-5}{{12}}(25 - 20) = \frac{{505}}{24}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{23}} \in [25;30)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 25 + \frac{{\frac{{3.30}}{4} - (5 + 12)}}{8}(30 - 25) = \frac{{455}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{355}}{{48}}\)
Vì \(\frac{{355}}{{48}}>3\) nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An
- KP2
- TH2
- TH3
- VD
Trả lời câu hỏi Khám phá 2 trang 70 SGK Toán 12 Chân trời sáng tạo
Kết quả điều tra tổng thu nhập trong năm 2022 của một số hộ gia đình trong một địa phương được ghi lại ở bảng sau:

a) Hãy tìm các tứ phân vị \({Q_1}\) và \({Q_3}\).
b) Một doanh nghiệp địa phương muốn hướng dịch vụ của mình đến các gia đình có mức thu nhập ở tầm trung, tức là 50% các hộ gia đình có mức thu nhập ở chính giữa so với tất cả các hộ gia đình của địa phương. Hỏi doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng nào?
Phương pháp giải:
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Lời giải chi tiết:
a) Cỡ mẫu n = 150
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{150}}\) là mẫu số liệu gốc gồm thu nhập của 150 hộ gia đình được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{24}} \in [200;250)\); \({x_{25}}; \ldots ;{\rm{ }}{x_{86}} \in [250;300)\); \({x_{87}}; \ldots ;{\rm{ }}{x_{120}} \in [300;350)\); \({x_{121}}; \ldots ;{\rm{ }}{x_{141}} \in [350;400)\); \({x_{142}}; \ldots ;{\rm{ }}{x_{150}} \in [400;450)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_{38}} \in [250;300)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 250 + \frac{{\frac{{150}}{4} - 24}}{{62}}(300 - 250) = \frac{{16175}}{{62}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{113}} \in [300;350)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 300 + \frac{{\frac{{3.150}}{4} - (24 + 62)}}{{34}}(350 - 300) = \frac{{11525}}{{34}}\)
b) Doanh nghiệp cần hướng đến các gia đình có mức thu nhập trong khoảng \([{Q_1};{Q_3}) = [260,89;338,97)\)(triệu đồng)
Trả lời câu hỏi Thực hành 2 trang 71 SGK Toán 12 Chân trời sáng tạo
Hãy so sánh khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình và bác An trong Khởi động.
Phương pháp giải:
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
Lời giải chi tiết:
Cỡ mẫu \(n = 30\);
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác An được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}} \in [20;25)\); \({x_{26}}; \ldots ;{\rm{ }}{x_{30}} \in [25;30)\);
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 20 + \frac{{\frac{{30}}{4}}}{{25}}(25 - 20) = \frac{{43}}{2}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{23}} \in [20;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 20 + \frac{{\frac{{3.30}}{4}}}{{25}}(25 - 20) = \frac{{49}}{2}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = 3\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{30}}\) là mẫu số liệu gốc về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [15;20)\); \({y_6}; \ldots ;{\rm{ }}{y_{17}} \in [20;25)\);\({y_{18}}; \ldots ;{\rm{ }}{y_{25}} \in [25;30)\);\({y_{26}};{y_{27}};{\rm{ }}{y_{28}} \in [30;35)\);\({y_{29}};{y_{30}} \in [35;40)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({y_8} \in [20;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 20 + \frac{{\frac{{30}}{4}}-5}{{12}}(25 - 20) = \frac{{505}}{24}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{23}} \in [25;30)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 25 + \frac{{\frac{{3.30}}{4} - (5 + 12)}}{8}(30 - 25) = \frac{{455}}{{16}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{355}}{{48}}\)
Vì \(\frac{{355}}{{48}}>3\) nên khoảng tứ phân vị của mẫu số liệu ghép nhóm về thời gian tập thể dục buổi sáng mỗi ngày của bác Bình lớn hơn bác An
Trả lời câu hỏi Thực hành 3 trang 73 SGK Toán 12 Chân trời sáng tạo
a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu ghép nhóm ở Ví dụ 4 sau khi đã loại bỏ các giá trị ngoại lệ. Em có nhận xét gì về khoảng biến thiên, khoảng tứ phân vị vừa tìm được và khoảng biến thiên, khoảng tứ phân vị ban đầu?
Hằng ngày ông Thắng đều đi xe buýt từ nhà đến cơ quan. Dưới đây là bảng thống kê thời gian của 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan.

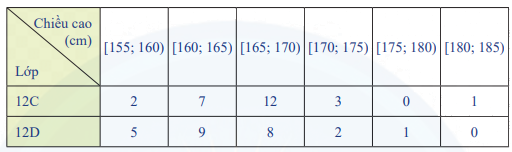
b) Hãy so sánh độ phân tán của nửa giữa hai mẫu số liệu chiều cao của các học sinh nữ lớp 12C và 12D ở Thực hành 1.
Phương pháp giải:
a) Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\)
Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Tìm khoảng tứ phân vị của 2 nhóm số liệu rồi so sánh
Lời giải chi tiết:
a) Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc gồm thời gian 100 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm.
Khoảng biến thiên R = 33 – 15 = 18 (phút).
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{22}} \in [15;18)\); \({x_{23}}; \ldots ;{\rm{ }}{x_{60}} \in [18;21)\); \({x_{61}}; \ldots ;{\rm{ }}{x_{87}} \in [21;24)\); \({x_{88}}; \ldots ;{\rm{ }}{x_{95}} \in [24;27)\);\({x_{96}}; \ldots ;{\rm{ }}{x_{99}} \in [27;30)\);\({x_{100}} \in [30;33)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [18;21)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 18 + \frac{{\frac{{100}}{4} - 22}}{{38}}(21 - 18) = \frac{{693}}{{38}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [21;24)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 21 + \frac{{\frac{{3.100}}{4} - (22 + 38)}}{{27}}(24 - 21) = \frac{{68}}{3}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{505}}{{114}}\).
Giá trị x trong mẫu số liệu là giá trị ngoại lệ nếu \(x > {Q_3} + 1,5{\Delta _Q}\) hoặc \(x < {Q_1} - 1,5{\Delta _Q}\).
Hay \(x > \frac{{68}}{3} + 1,5.\frac{{505}}{{114}} = 29,31\) hoặc \(x < \frac{{693}}{{38}} - 1,5.\frac{{505}}{{114}} = 11,59\).
Do đó, chỉ có đúng 1 lần ông Thắng đi hết 32 phút là giá trị ngoại lệ của mẫu số liệu ghép nhóm.
Khoảng biến thiên của mẫu số liệu ghép nhóm sau khi loại bỏ giá trị ngoại lệ: 30 – 15 = 15 (phút).
Gọi \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{99}}\) là mẫu số liệu gốc gồm thời gian 99 lần ông Thắng đi xe buýt từ nhà đến cơ quan được xếp theo thứ tự không giảm, sau khi đã loại bỏ giá trị ngoại lệ.
Ta có: \({z_1};{\rm{ }}{z_2}; \ldots ;{\rm{ }}{z_{22}} \in [15;18)\); \({z_{23}}; \ldots ;{\rm{ }}{z_{60}} \in [18;21); {z_{61}}; \ldots ;{\rm{ }}{z_{87}} \in [21;24); {z_{88}}; \ldots ;{\rm{ }}{z_{95}} \in [24;27); {z_{95}}; \ldots ;{\rm{ }}{z_{99}} \in [27;30) \).
Tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}'' = 18 + \frac{{\frac{{99}}{4}}-22}{{38}}(21 - 18) = \frac{{2769}}{{152}}\).
Tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}'' = 21 + \frac{{\frac{{3.99}}{4} - (22+38)}}{{27}}(24 - 21) = \frac{{271}}{{12}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}'' = {Q_3}'' - {Q_1}'' = \frac{{1991}}{{456}}\).
Nhận xét: Sau khi loại bỏ giá trị ngoại lệ, khoảng biến thiên mới giảm mạnh còn khoảng tứ phân vị mới không bị ảnh hưởng nhiều.
b) Cỡ mẫu \(n = 25\).
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12C được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2} \in [155;160)\); \({x_3}; \ldots ;{\rm{ }}{x_9} \in [160;165)\);\({x_{10}}; \ldots ;{\rm{ }}{x_{21}} \in [165;170)\);\({x_{22}}; \ldots ;{\rm{ }}{x_{24}} \in [170;175)\);\({x_{25}} \in [180;185)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_6} + {x_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 160 + \frac{{\frac{{25}}{4} - 2}}{7}(165 - 160) = \frac{{4565}}{{28}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 165 + \frac{{\frac{{3.25}}{4} - (2 + 7)}}{{12}}(170 - 165) = \frac{{2705}}{{16}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{675}}{{112}}\).
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{25}}\) là mẫu số liệu gốc về chiều cao của các bạn học sinh nữ lớp 12D được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_5} \in [155;160)\); \({y_6}; \ldots ;{\rm{ }}{y_{14}} \in [160;165)\);\({y_{15}}; \ldots ;{\rm{ }}{y_{22}} \in [165;170)\);\({y_{23}};{\rm{ }}{{\rm{y}}_{24}} \in [170;175)\);\({y_{25}} \in [175;180)\).
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_6} + {y_7}) \in [160;165)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 160 + \frac{{\frac{{25}}{4} - 5}}{9}(165 - 160) = \frac{{5785}}{{36}}\).
Tứ phân vị thứ ba của mẫu số liệu gốc là \({y_{19}} \in [165;170)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 165 + \frac{{\frac{{3.25}}{4} - (5 + 9)}}{8}(170 - 165) = \frac{{5375}}{{32}}\).
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{2095}}{{288}}\).
Có \({\Delta _Q}' > {\Delta _Q}\) nên chiều cao của các bạn học sinh nữ lớp 12D có độ phân tán lơn hơn lớp 12C.
Trả lời câu hỏi Vận dụng trang 73 SGK Toán 12 Chân trời sáng tạo
Giả sử kết quả khảo sát hai khu vực A và B về độ tuổi kết hôn của một số phụ nữ vừa lập gia đình được cho ở bảng sau:

a) Hãy tìm khoảng biến thiên và khoảng tứ phân vị của từng mẫu số liệu ghép nhóm ứng với mỗi khu vực A và B.
b) Nếu so sánh theo khoảng tứ phân vị thì phụ nữ ở khu vực nào có độ tuổi kết hôn đồng đều hơn?
Phương pháp giải:
a) Khoảng biến thiên của mẫu số liệu ghép nhóm là hiệu số giữa đầu mút phải của nhóm cuối cùng và đầu mút trái của nhóm đầu tiên có chứa dữ liệu của mẫu số liệu.
Tứ phân vị thứ k, kí hiệu là \({Q_k}\), với k = 1, 2, 3 của mẫu số liệu ghép nhóm được xác định như sau:
\({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}({u_{m + 1}} - {u_m})\)
trong đó:
\(n = {n_1} + {n_2} + {n_3} + ... + {n_k}\) là cỡ mẫu
\([{u_m};{u_{m + 1}}]\) là nhóm chứa tứ phân vị thứ k
\({n_m}\) là tần số của nhóm chứa tứ phân vị thứ k
\(C = {n_1} + {n_2} + {n_3} + ... + {n_{m - 1}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm, kí hiệu \({\Delta _Q}\), là hiệu giữa tứ phân vị thứ ba \({Q_3}\) và tứ phân vị thứ nhất \({Q_1}\) của mẫu số liệu ghép nhóm đó, tức là \({\Delta _Q} = {Q_3} - {Q_1}\).
b) Khoảng tứ phân vị càng bé thì dữ liệu càng tập trung xung quanh trung vị
Lời giải chi tiết:
Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực A là: 34 – 19 = 15(tuổi)
Khoảng biến thiên của mẫu số liệu ghép nhóm ứng với khu vực B là: 31 – 19 = 12(tuổi)
Cỡ mẫu \(n = 100\)
Gọi \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực A được xếp theo thứ tự không giảm.
Ta có: \({x_1};{\rm{ }}{x_2}; \ldots ;{\rm{ }}{x_{10}} \in [19;22)\); \({x_{11}}; \ldots ;{\rm{ }}{x_{37}} \in [22;25)\);\({x_{38}}; \ldots ;{\rm{ }}{x_{68}} \in [25;28)\);\({x_{69}}; \ldots ;{\rm{ }}{x_{93}} \in [28;31)\);\({x_{94}}; \ldots ;{\rm{ }}{x_{100}} \in [31;34)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({x_{25}} + {x_{26}}) \in [22;25)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1} = 22 + \frac{{\frac{{100}}{4} - 10}}{{27}}(25 - 22) = \frac{{71}}{3}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({x_{75}} + {x_{76}}) \in [28;31)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3} = 28 + \frac{{\frac{{3.100}}{4} - (10 + 27 + 31)}}{{25}}(31 - 28) = \frac{{721}}{{25}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q} = {Q_3} - {Q_1} = \frac{{388}}{{75}}\)
Gọi \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{100}}\) là mẫu số liệu gốc về độ tuổi kết hôn của phụ nữ ở khu vực B được xếp theo thứ tự không giảm.
Ta có: \({y_1};{\rm{ }}{y_2}; \ldots ;{\rm{ }}{y_{47}} \in [19;22)\); \({y_{48}}; \ldots ;{\rm{ }}{y_{87}} \in [22;25)\);\({y_{88}}; \ldots ;{\rm{ }}{y_{98}} \in [25;30)\);\({y_{99}};{y_{100}} \in [28;31)\)
Tứ phân vị thứ nhất của mẫu số liệu gốc là \(\frac{1}{2}({y_{25}} + {y_{26}}) \in [19;22)\). Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: \({Q_1}' = 19 + \frac{{\frac{{100}}{4}}}{{47}}(22 - 19) = \frac{{968}}{{47}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \(\frac{1}{2}({y_{75}} + {y_{76}}) \in [22;25)\). Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: \({Q_3}' = 22 + \frac{{\frac{{3.100}}{4} - 47}}{{40}}(25 - 22) = \frac{{241}}{{10}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là: \({\Delta _Q}' = {Q_3}' - {Q_1}' = \frac{{1647}}{{470}}\)
b) Có \({\Delta _Q}' < {\Delta _Q}\) nên phụ nữ ở khu vực B có độ tuổi kết hôn đồng đều hơn
Giải mục 2 trang 70, 71, 72 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của SGK Toán 12 tập 1 Chân trời sáng tạo thường tập trung vào một chủ đề quan trọng trong chương trình học. Việc nắm vững kiến thức và kỹ năng trong mục này là nền tảng để giải quyết các bài toán phức tạp hơn ở các chương tiếp theo. Bài viết này sẽ cung cấp lời giải chi tiết cho từng bài tập trong mục 2, trang 70, 71, 72, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài.
Nội dung chính của Mục 2
Trước khi đi vào giải bài tập, chúng ta cần nắm vững nội dung chính của Mục 2. Thông thường, mục này sẽ trình bày về:
- Các khái niệm cơ bản liên quan đến chủ đề.
- Các định lý, tính chất quan trọng.
- Các ví dụ minh họa cách áp dụng kiến thức vào giải bài tập.
Giải chi tiết bài tập trang 70
Bài 1: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Bài 2: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Bài 3: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Giải chi tiết bài tập trang 71
Bài 4: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Bài 5: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Giải chi tiết bài tập trang 72
Bài 6: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Bài 7: (Nêu đề bài và giải chi tiết từng bước. Sử dụng các ký hiệu toán học và giải thích rõ ràng.)
Mẹo giải bài tập hiệu quả
- Đọc kỹ đề bài và xác định yêu cầu của bài toán.
- Phân tích các dữ kiện đã cho và tìm mối liên hệ giữa chúng.
- Chọn phương pháp giải phù hợp.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Lưu ý quan trọng
Trong quá trình giải bài tập, các em cần chú ý đến việc:
- Sử dụng đúng các ký hiệu toán học.
- Trình bày lời giải một cách rõ ràng, logic.
- Kiểm tra lại các bước giải để tránh sai sót.
Tusach.vn – Đồng hành cùng học sinh
Tusach.vn cam kết cung cấp lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1 Chân trời sáng tạo. Chúng tôi hy vọng rằng với sự hỗ trợ của Tusach.vn, các em sẽ học tập hiệu quả và đạt kết quả cao trong môn Toán.
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.
| Chủ đề | Trang |
|---|---|
| Mục 2 | 70-72 |