Giải mục 2 trang 43,44,45 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 2 trang 43,44,45 SGK Toán 12 tập 1 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 2 trang 43,44,45 SGK Toán 12 tập 1 chương trình Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em hiểu rõ bản chất của bài toán, từ đó áp dụng kiến thức vào các bài tập khác một cách hiệu quả.
Tổng và hiệu của hai vectơ
TH3
Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} \)
Phương pháp giải:
Áp dụng quy tắc hình bình hành, hình hộp và 2 vecto bằng nhau
Lời giải chi tiết:
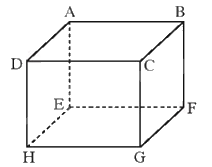
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} = \overrightarrow {DB} + \overrightarrow {DH} = \overrightarrow {DF} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} = \overrightarrow {HE} + \overrightarrow {HD} + \overrightarrow {HG} = \overrightarrow {HB} \)
TH4
Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm các vectơ hiệu \(\overrightarrow {AS} - \overrightarrow {DC} ,\overrightarrow {CS} - \overrightarrow {DA} \)
Phương pháp giải:
Áp dụng quy tắc hiệu và 2 vecto bằng nhau
Lời giải chi tiết:
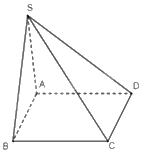
\(\overrightarrow {AS} - \overrightarrow {DC} = \overrightarrow {AS} - \overrightarrow {AB} = \overrightarrow {AS} + \overrightarrow {BA} = \overrightarrow {BS} \)
\(\overrightarrow {CS} - \overrightarrow {DA} = \overrightarrow {CS} - \overrightarrow {CB} = \overrightarrow {CS} + \overrightarrow {BC} = \overrightarrow {BS} \)
KP2
Trả lời câu hỏi Khám phá 2 trang 43 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′ (Hình 5).
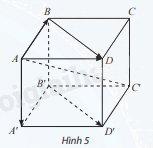
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
b) So sánh hai vectơ \(\overrightarrow {BD'} ,\overrightarrow {B'D'} \)
c) Giải thích tại sao \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AD} \).
Phương pháp giải:
Áp dụng quy tắc hình bình hành và quy tắc ba điểm
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {BD'} = \overrightarrow {B'D'} \)
c) \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
TH6
Trả lời câu hỏi Thực hành 6 trang 46 SGK Toán 12 Chân trời sáng tạo
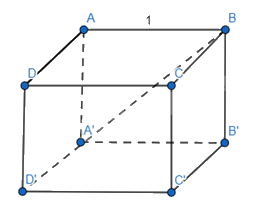
Cho hình lập phương ABCD. A′B′C′D′ có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \)
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} \)
Phương pháp giải:
Áp dụng quy tắc hình hộp và định lí Pytago
Lời giải chi tiết:
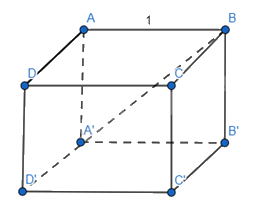
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
\(|\overrightarrow a | = |\overrightarrow {BD'} | = \sqrt {B{D^2} + D{D^2}} = \sqrt {B{A^2} + B{C^2} + D{D^2}} = \sqrt {1 + 1 + 1} = \sqrt 3 \)
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} = \overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {C'A} = \overrightarrow {CC'} \)
\(|\overrightarrow b | = |\overrightarrow {CC'} | = 1\)
TH5
Trả lời câu hỏi Thực hành 5 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Hãy thực hiện các phép toán sau đây:
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} \)
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} \)
Phương pháp giải:
Áp dụng quy tắc ba điểm, quy tắc hiệu và tính chất trung điểm
Lời giải chi tiết:
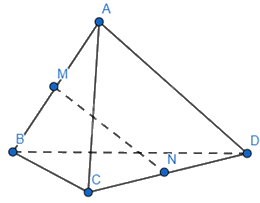
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} = \overrightarrow {MC} + \overrightarrow {CN} = \overrightarrow {MN} \)
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {MA} + \overrightarrow {DN} = \overrightarrow {MD} + \overrightarrow {DN} = \overrightarrow {MN} \)
KP3
Trả lời câu hỏi Khám phá 3 trang 44 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′.
a) Tìm các vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \), \(\overrightarrow {AC} + \overrightarrow {AA'} \)
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} \)
Phương pháp giải:
Áp dụng quy tắc hình bình hành và tính chất kết hợp của phép cộng
Lời giải chi tiết:
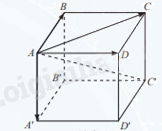
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
VD2
Trả lời câu hỏi Vận dụng 2 trang 46 SGK Toán 12 Chân trời sáng tạo
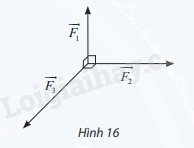
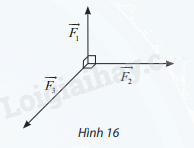
Ba lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N (Hình 16). Tính độ lớn hợp lực của ba lực đã cho.
Phương pháp giải:
Áp dụng quy tắc hình bình hành và định lí Pytago
Lời giải chi tiết:
Ta có: \(|\overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_2}^2 + {F_3}^2} = \sqrt {{3^2} + {4^2}} = 5\)
Độ lớn hợp lực của ba lực là: \(|\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_1}^2 + {5^2}} = \sqrt {{2^2} + {5^2}} = \sqrt {29} N\)
- KP2
- KP3
- TH3
- TH4
- TH5
- TH6
- VD2
Trả lời câu hỏi Khám phá 2 trang 43 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′ (Hình 5).
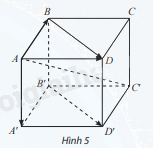
a) Trong mặt phẳng (ABCD), tìm vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \)
b) So sánh hai vectơ \(\overrightarrow {BD'} ,\overrightarrow {B'D'} \)
c) Giải thích tại sao \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AD} \).
Phương pháp giải:
Áp dụng quy tắc hình bình hành và quy tắc ba điểm
Lời giải chi tiết:
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
b) \(\overrightarrow {BD'} = \overrightarrow {B'D'} \)
c) \(\overrightarrow {AB} + \overrightarrow {B'D'} = \overrightarrow {AB} + \overrightarrow {BD} = \overrightarrow {AD} \)
Trả lời câu hỏi Khám phá 3 trang 44 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.A′B′C′D′.
a) Tìm các vectơ tổng \(\overrightarrow {AB} + \overrightarrow {AD} \), \(\overrightarrow {AC} + \overrightarrow {AA'} \)
b) Dùng kết quả của câu a và tính chất kết hợp của phép cộng vectơ để chứng minh \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} \)
Phương pháp giải:
Áp dụng quy tắc hình bình hành và tính chất kết hợp của phép cộng
Lời giải chi tiết:
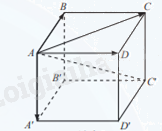
a) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);\(\overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
b) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC} + \overrightarrow {AA'} = \overrightarrow {AC'} \)
Trả lời câu hỏi Thực hành 3 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình hộp ABCD.EFGH. Thực hiện các phép toán sau đây:
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} \)
Phương pháp giải:
Áp dụng quy tắc hình bình hành, hình hộp và 2 vecto bằng nhau
Lời giải chi tiết:
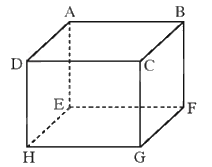
a) \(\overrightarrow {DA} + \overrightarrow {DC} + \overrightarrow {DH} = \overrightarrow {DB} + \overrightarrow {DH} = \overrightarrow {DF} \)
b) \(\overrightarrow {HE} + \overrightarrow {GC} + \overrightarrow {AB} = \overrightarrow {HE} + \overrightarrow {HD} + \overrightarrow {HG} = \overrightarrow {HB} \)
Trả lời câu hỏi Thực hành 4 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình chóp S.ABCD có đáy là hình bình hành. Tìm các vectơ hiệu \(\overrightarrow {AS} - \overrightarrow {DC} ,\overrightarrow {CS} - \overrightarrow {DA} \)
Phương pháp giải:
Áp dụng quy tắc hiệu và 2 vecto bằng nhau
Lời giải chi tiết:
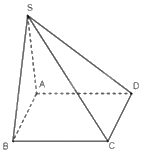
\(\overrightarrow {AS} - \overrightarrow {DC} = \overrightarrow {AS} - \overrightarrow {AB} = \overrightarrow {AS} + \overrightarrow {BA} = \overrightarrow {BS} \)
\(\overrightarrow {CS} - \overrightarrow {DA} = \overrightarrow {CS} - \overrightarrow {CB} = \overrightarrow {CS} + \overrightarrow {BC} = \overrightarrow {BS} \)
Trả lời câu hỏi Thực hành 5 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Hãy thực hiện các phép toán sau đây:
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} \)
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} \)
Phương pháp giải:
Áp dụng quy tắc ba điểm, quy tắc hiệu và tính chất trung điểm
Lời giải chi tiết:
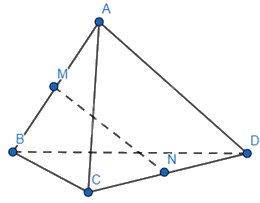
a) \(\overrightarrow {BM} + \overrightarrow {AC} + \overrightarrow {ND} = \overrightarrow {MA} + \overrightarrow {AC} + \overrightarrow {CN} = \overrightarrow {MC} + \overrightarrow {CN} = \overrightarrow {MN} \)
b) \(\overrightarrow {AD} - \overrightarrow {AM} + \overrightarrow {NC} = \overrightarrow {AD} + \overrightarrow {MA} + \overrightarrow {DN} = \overrightarrow {MD} + \overrightarrow {DN} = \overrightarrow {MN} \)
Trả lời câu hỏi Thực hành 6 trang 46 SGK Toán 12 Chân trời sáng tạo
Cho hình lập phương ABCD. A′B′C′D′ có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây:
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} \)
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} \)
Phương pháp giải:
Áp dụng quy tắc hình hộp và định lí Pytago
Lời giải chi tiết:
a) \(\overrightarrow a = \overrightarrow {BA} + \overrightarrow {BC} + \overrightarrow {BB'} = \overrightarrow {BD'} \)
\(|\overrightarrow a | = |\overrightarrow {BD'} | = \sqrt {B{D^2} + D{D^2}} = \sqrt {B{A^2} + B{C^2} + D{D^2}} = \sqrt {1 + 1 + 1} = \sqrt 3 \)
b) \(\overrightarrow b = \overrightarrow {BC} - \overrightarrow {BA} + \overrightarrow {C'A} = \overrightarrow {BC} + \overrightarrow {AB} + \overrightarrow {C'A} = \overrightarrow {CC'} \)
\(|\overrightarrow b | = |\overrightarrow {CC'} | = 1\)
Trả lời câu hỏi Vận dụng 2 trang 46 SGK Toán 12 Chân trời sáng tạo
Ba lực \(\overrightarrow {{F_1}} ;\overrightarrow {{F_2}} ;\overrightarrow {{F_3}} \) cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn lần lượt là 2N; 3N; 4N (Hình 16). Tính độ lớn hợp lực của ba lực đã cho.
Phương pháp giải:
Áp dụng quy tắc hình bình hành và định lí Pytago
Lời giải chi tiết:
Ta có: \(|\overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_2}^2 + {F_3}^2} = \sqrt {{3^2} + {4^2}} = 5\)
Độ lớn hợp lực của ba lực là: \(|\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} | = \sqrt {{F_1}^2 + {5^2}} = \sqrt {{2^2} + {5^2}} = \sqrt {29} N\)
Giải mục 2 trang 43,44,45 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Hướng dẫn chi tiết
Mục 2 của chương trình Toán 12 tập 1 Chân trời sáng tạo tập trung vào việc nghiên cứu về giới hạn của hàm số. Đây là một khái niệm nền tảng quan trọng, mở đầu cho chương trình Giải tích. Việc nắm vững kiến thức về giới hạn sẽ giúp học sinh hiểu sâu hơn về các khái niệm tiếp theo như đạo hàm, tích phân.
Nội dung chính của Mục 2 trang 43,44,45
- Khái niệm giới hạn của hàm số tại một điểm: Học sinh sẽ được làm quen với định nghĩa giới hạn, hiểu ý nghĩa của việc hàm số tiến tới một giá trị khi x tiến tới một điểm nhất định.
- Tính chất của giới hạn: Các tính chất như giới hạn của tổng, hiệu, tích, thương, và giới hạn của hàm hợp sẽ được trình bày và minh họa bằng các ví dụ cụ thể.
- Các dạng giới hạn cơ bản: Học sinh sẽ được hướng dẫn cách tính giới hạn của các hàm số đơn giản, sử dụng các quy tắc và công thức đã học.
- Ứng dụng của giới hạn: Giới hạn được sử dụng để giải quyết các bài toán liên quan đến sự liên tục của hàm số, và là cơ sở để tính đạo hàm.
Giải chi tiết các bài tập trong Mục 2
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 2 trang 43,44,45 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: Tính các giới hạn sau
lim (x→2) (x^2 + 3x - 1)
Lời giải: Thay x = 2 vào biểu thức, ta được: 2^2 + 3*2 - 1 = 4 + 6 - 1 = 9. Vậy lim (x→2) (x^2 + 3x - 1) = 9.
lim (x→-1) (x^3 - 2x + 5)
Lời giải: Thay x = -1 vào biểu thức, ta được: (-1)^3 - 2*(-1) + 5 = -1 + 2 + 5 = 6. Vậy lim (x→-1) (x^3 - 2x + 5) = 6.
Bài 2: Tính các giới hạn sau
(Các bài tập tiếp theo sẽ được giải tương tự, áp dụng các quy tắc và tính chất đã học về giới hạn.)
Mẹo giải bài tập về giới hạn
- Nắm vững định nghĩa: Hiểu rõ định nghĩa giới hạn là bước đầu tiên để giải quyết các bài toán liên quan.
- Sử dụng các tính chất: Áp dụng các tính chất của giới hạn để đơn giản hóa biểu thức và tính toán nhanh chóng.
- Phân tích kỹ đề bài: Xác định rõ dạng giới hạn cần tính và lựa chọn phương pháp phù hợp.
- Kiểm tra lại kết quả: Sau khi tính toán, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài SGK Toán 12 tập 1 Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về giới hạn:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến
- Video bài giảng trên YouTube
Tusach.vn hy vọng rằng với lời giải chi tiết và hướng dẫn cụ thể này, các em sẽ tự tin hơn trong việc giải các bài tập về giới hạn của hàm số. Chúc các em học tập tốt!