Giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo là một phần quan trọng trong quá trình ôn tập và củng cố kiến thức về giới hạn của hàm số.
tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp các em học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Khảo sát và vẽ đồ thị của các hàm số sau: a) \(y = 3 + \frac{1}{x}\) b) \(y = \frac{{x - 3}}{{1 - x}}\)
Đề bài
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = 3 + \frac{1}{x}\)
b) \(y = \frac{{x - 3}}{{1 - x}}\)
Phương pháp giải - Xem chi tiết
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm giới hạn tại vô cực, giới hạn vô cực và các tiệm cận của đồ thị hàm số (nếu có)
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết
a) \(y = 3 + \frac{1}{x}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 0\} \)
- Chiều biến thiên:
\(y' = - \frac{1}{{{x^2}}} < 0\forall x \in D\) nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } (3 + \frac{1}{x}) = 3;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } (3 + \frac{1}{x}) = 3\) nên y = 3 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {0^ + }} y = \mathop {\lim }\limits_{x \to {0^ + }} (3 + \frac{1}{x}) = + \infty ;\mathop {\lim }\limits_{x \to {0^ - }} y = \mathop {\lim }\limits_{x \to {0^ - }} (3 + \frac{1}{x}) = - \infty \) nên x = 0 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
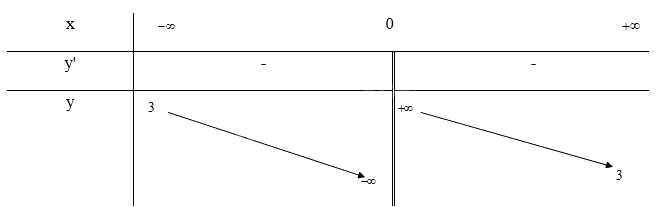
Ta có: \(y = 0 \Leftrightarrow 3 + \frac{1}{x} = 0 \Leftrightarrow x = - \frac{1}{3}\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (\( - \frac{1}{3}\); 0)
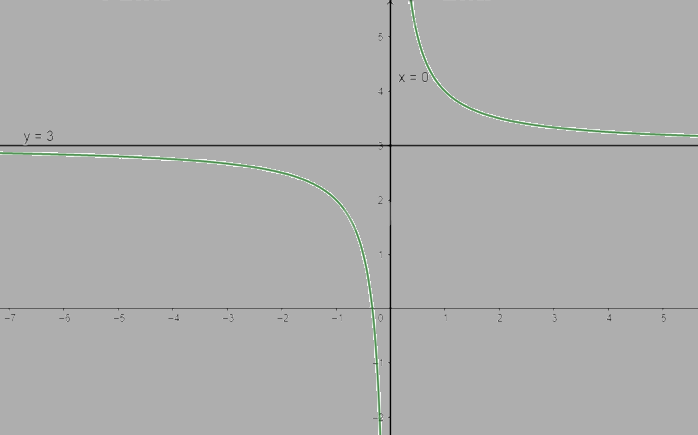
b) \(y = \frac{{x - 3}}{{1 - x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
- Chiều biến thiên:
\(y' = \frac{{ - 2}}{{{{(1 - x)}^2}}} < 0\forall x \in D\) nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 3}}{{1 - x}} = - 1\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 3}}{{1 - x}} = - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x - 3}}{{1 - x}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x - 3}}{{1 - x}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
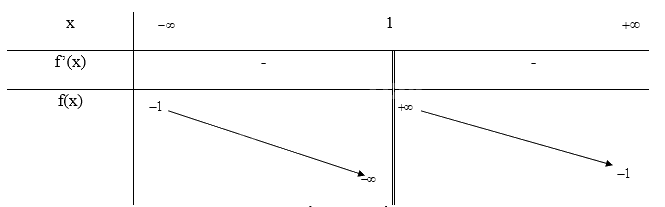
Khi x = 0 thì y = -3 nên (0; -3) là giao của đồ thị hàm số với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{x - 3}}{{1 - x}} = 0 \Leftrightarrow x = 3\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (3; 0)
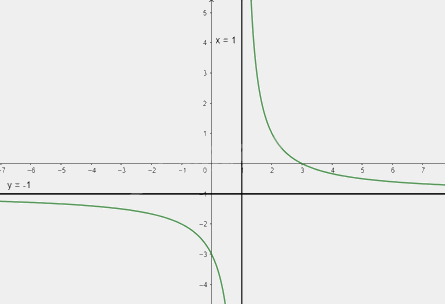
Giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Việc nắm vững phương pháp giải các bài tập về giới hạn sẽ giúp học sinh tự tin hơn trong các kỳ thi và ứng dụng vào thực tế.
Nội dung bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 yêu cầu tính các giới hạn sau:
- lim (x→2) (x² - 3x + 2) / (x - 2)
- lim (x→-1) (x³ + 1) / (x + 1)
- lim (x→0) (√(x+1) - 1) / x
Phương pháp giải bài tập về giới hạn
Để giải các bài tập về giới hạn, chúng ta có thể sử dụng một số phương pháp sau:
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào biểu thức để tính giới hạn. Tuy nhiên, phương pháp này chỉ áp dụng được khi biểu thức xác định tại giá trị x đó.
- Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức, sau đó thay giá trị của x vào để tính giới hạn.
- Phương pháp nhân liên hợp: Nhân cả tử số và mẫu số với liên hợp của biểu thức để khử dạng vô định.
- Quy tắc L'Hopital: Nếu giới hạn có dạng 0/0 hoặc ∞/∞, ta có thể áp dụng quy tắc L'Hopital để tính giới hạn bằng cách lấy đạo hàm của tử số và mẫu số.
Lời giải chi tiết bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo
1. lim (x→2) (x² - 3x + 2) / (x - 2)
Ta phân tích tử số thành nhân tử: x² - 3x + 2 = (x - 1)(x - 2)
Vậy, lim (x→2) (x² - 3x + 2) / (x - 2) = lim (x→2) (x - 1)(x - 2) / (x - 2) = lim (x→2) (x - 1) = 2 - 1 = 1
2. lim (x→-1) (x³ + 1) / (x + 1)
Ta phân tích tử số thành nhân tử: x³ + 1 = (x + 1)(x² - x + 1)
Vậy, lim (x→-1) (x³ + 1) / (x + 1) = lim (x→-1) (x + 1)(x² - x + 1) / (x + 1) = lim (x→-1) (x² - x + 1) = (-1)² - (-1) + 1 = 1 + 1 + 1 = 3
3. lim (x→0) (√(x+1) - 1) / x
Ta nhân cả tử số và mẫu số với liên hợp của tử số: (√(x+1) - 1) / x = ((√(x+1) - 1)(√(x+1) + 1)) / (x(√(x+1) + 1)) = (x + 1 - 1) / (x(√(x+1) + 1)) = x / (x(√(x+1) + 1)) = 1 / (√(x+1) + 1)
Vậy, lim (x→0) (√(x+1) - 1) / x = lim (x→0) 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2
Kết luận
Thông qua việc giải bài tập 3 trang 36 SGK Toán 12 tập 1 - Chân trời sáng tạo, chúng ta đã củng cố kiến thức về các phương pháp tính giới hạn. Hy vọng rằng, với lời giải chi tiết và dễ hiểu này, các em học sinh sẽ tự tin hơn trong việc giải các bài tập tương tự và đạt kết quả tốt trong học tập.
Lưu ý: Nếu bạn gặp khó khăn trong quá trình học tập, đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên, bạn bè hoặc các nguồn tài liệu học tập uy tín.