Lý thuyết Phương trình mặt cầu Toán 12 Chân trời sáng tạo
Tổng quan nội dung
Lý Thuyết Phương Trình Mặt Cầu Toán 12 Chân Trời Sáng Tạo
Phương trình mặt cầu là một trong những kiến thức quan trọng trong chương trình Toán 12 Chân trời sáng tạo. Nắm vững lý thuyết này giúp học sinh giải quyết các bài toán liên quan đến hình học không gian một cách hiệu quả.
Bài viết này sẽ cung cấp đầy đủ và chi tiết lý thuyết về phương trình mặt cầu, cùng với các ví dụ minh họa và bài tập thực hành để bạn có thể hiểu rõ và áp dụng kiến thức vào giải bài tập.
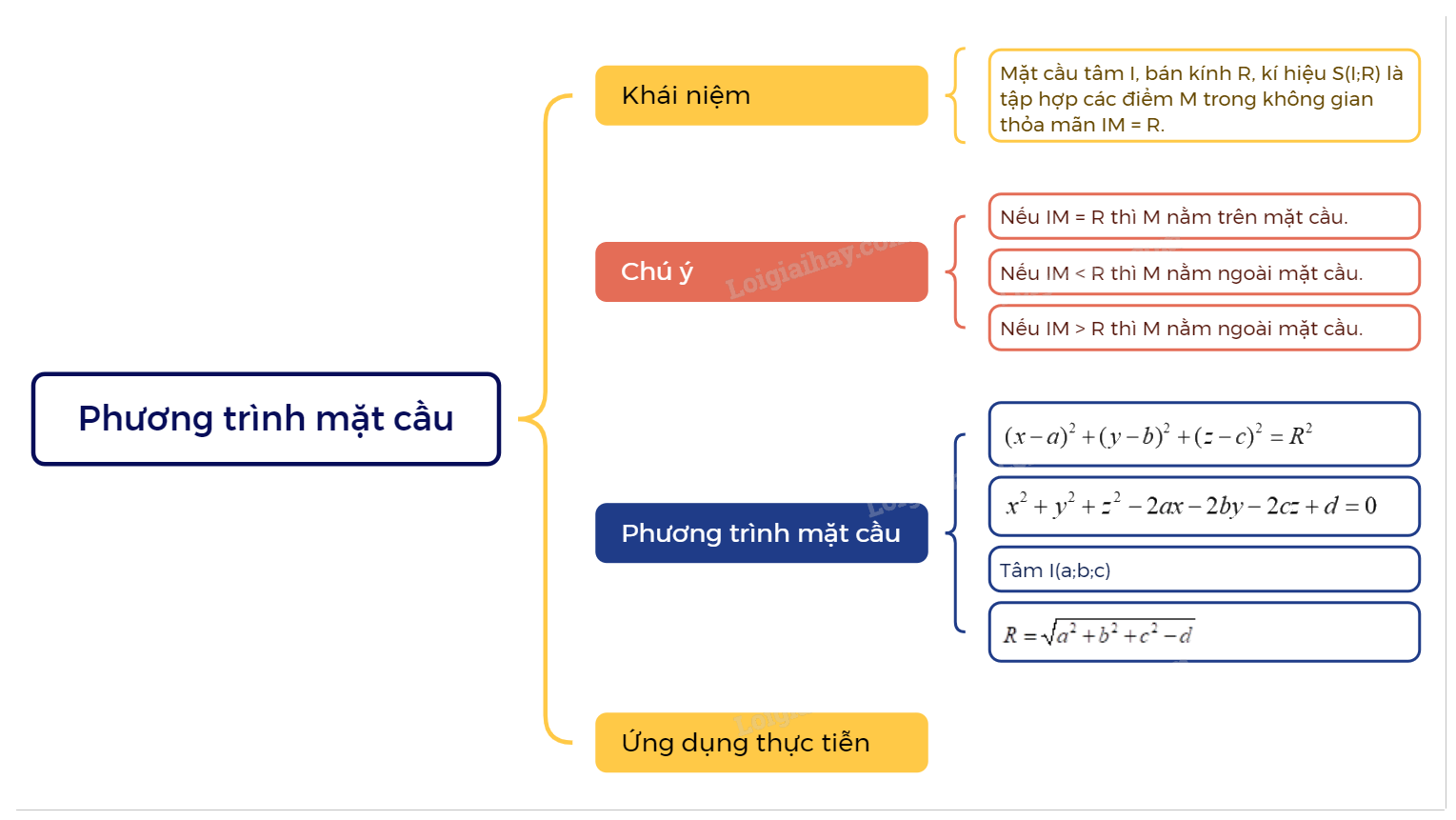
1. Phương trình mặt cầu trong không gian Khái niệm mặt cầu Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.
1. Phương trình mặt cầu trong không gian
Khái niệm mặt cầu
Trong không gian, cho điểm I và số dương R. Mặt cầu tâm I, bán kính R, kí hiệu S(I;R) là tập hợp các điểm M trong không gian thỏa mãn IM = R. Đoạn thẳng nối hai điểm thuộc mặt cầu và đi qua tâm I là đường kính mặt cầu.
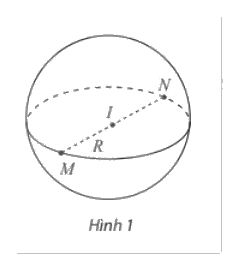
Chú ý: Cho mặt cầu S(I;R).
Nếu IM = R thì M nằm trên mặt cầu.
Nếu IM < R thì M nằm ngoài mặt cầu.
Nếu IM > R thì M nằm ngoài mặt cầu.
Phương trình mặt cầu
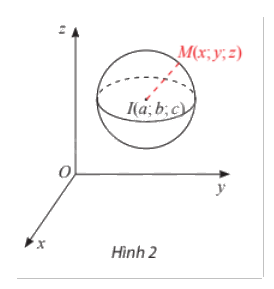
Trong không gian Oxyz, mặt cầu (S) tâm I(a;b;c) bán kính R có phương trình \({(x - a)^2} + {(y - b)^2} + {(z - c)^2} = {R^2}\) |
Nhận xét: Phương trình \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \({a^2} + {b^2} + {c^2} - d > 0\) là phương trình của mặt cầu tâm I(a;b;c) và bán kính \(R = \sqrt {{a^2} + {b^2} + {c^2} - d} \).
Ví dụ 1: Viết phương trình mặt cầu (S):
a) Có tâm I(1;2;3), bán kính R = 5.
b) Có đường kính AB với A(1;3;7) và B(3;5;1).
c) Có tâm A(1;0;2) và đi qua điểm B(2;4;1).
Giải:
a) Mặt cầu (S) có phương trình \({(x - 1)^2} + {(y - 2)^2} + {(z - 3)^3} = 25\).
b) Mặt cầu (S) có đường kính AB nên có tâm J(2;4;4) là trung điểm AB và bán kính R = JA = \(\sqrt {11} \).
Vậy (S) có phương trình \({(x - 2)^2} + {(y - 4)^2} + {(z - 4)^2} = 11\).
c) Mặt cầu (S) có tâm A(1;0;-2) và đi qua điểm B(2;4;1) nên có bán kính R = AB = \(\sqrt {26} \).
Vậy (S) có phương trình \({(x - 1)^2} + {y^2} + {(z + 2)^2} = 26\).
Ví dụ 2: Xác định tâm và bán kính mặt cầu có phương trình:
a) (S): \({(x - 3)^2} + {(y - 7)^2} + {(z + 1)^2} = 81\).
b) (S’): \({x^2} + {y^2} + {z^2} = 4\).
Giải:
a) Mặt cầu (S) có tâm I(3;7;-1) và bán kính R = \(\sqrt {81} \) = 9.
b) Mặt cầu (S’) có tâm O(0;0;0) và bán kính R’ = \(\sqrt 4 \) = 2.
Ví dụ 3: Trong các phương trình sau, phương trình nào là phương trình mặt cầu? Xác định tâm và bán kính mặt cầu đó.
a) \({x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\).
b) \({x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0\).
Giải:
a) Phương trình \({x^2} + {y^2} + {z^2} + 8x - 6y + 2z - 10 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - 4;b = 3;c = - 1;d = - 10\).
Ta có \({a^2} + {b^2} + {c^2} - d = 16 + 9 + 1 + 10 = 36 > 0\).
Suy ra phương trình đã cho là phương trình mặt cầu tâm I(-4;3;-1), bán kính R = 6.
b) Phương trình \({x^2} + {y^2} + {z^2} + x + y - 6z + 33 = 0\) có dạng \({x^2} + {y^2} + {z^2} - 2ax - 2by - 2cz + d = 0\) với \(a = - \frac{1}{2};b = - \frac{1}{2};c = 3;d = 33\).
Ta có \({a^2} + {b^2} + {c^2} - d = \frac{1}{4} + \frac{1}{4} + 9 - 33 = - \frac{{47}}{2} < 0\).
Suy ra phương trình đã cho không phải phương trình mặt cầu.
2. Vận dụng của phương trình mặt cầu
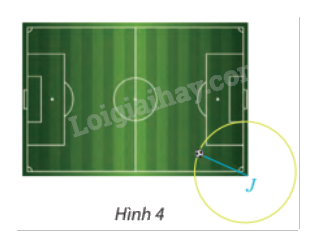
Ví dụ: Công nghệ hỗ trợ trọng tài VAR (Video Assisstant Referee) thiết lập một hệ tọa độ Oxyz để theo dõi vị trí của quả bóng M. Cho biết M đang nằm trên mặt sân có phương trình z = 0, đồng thời thuộc mặt cầu (S): \({(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\) (đơn vị độ dài tính theo mét).
a) Tìm tọa độ tâm I và bán kính R của mặt cầu (S).
b) Tìm tọa độ hình chiếu vuông góc J của tâm I trên mặt sân.
c) Tính khoảng cách từ vị trí M của quả bóng đến điểm J.
Giải:
Mặt cầu (S) có phương trình \({(x - 32)^2} + {(y - 50)^2} + {(z - 10)^2} = 109\) nên có tâm I(32;50;0) và bán kính \(R = \sqrt {109} \).
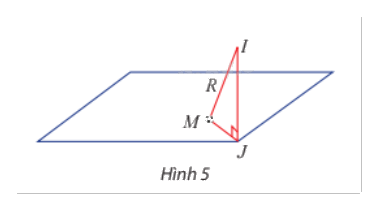
b) Trong không gian Oxyz, mặt sân có phương trình z = 0 trùng với mặt phẳng tọa độ (Oxy), suy ra hình chiếu vuông góc của điểm I(32;50;10) xuống mặt sân có tọa độ J(32;50;0).
c) Trong tam giác vuông IJM, ta có IJ = 10, IM = R, suy ra
\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {109 - 100} = 3\).
Vậy khoảng cách từ vị trí M của quả bóng đến điểm J là 3m.
Lý Thuyết Phương Trình Mặt Cầu Toán 12 Chân Trời Sáng Tạo: Tổng Quan
Trong chương trình Toán 12 Chân trời sáng tạo, phương trình mặt cầu là một chủ đề quan trọng thuộc phần hình học không gian. Hiểu rõ lý thuyết và cách áp dụng sẽ giúp học sinh giải quyết các bài toán một cách chính xác và hiệu quả. Bài viết này sẽ cung cấp một cái nhìn tổng quan và chi tiết về chủ đề này.
1. Định Nghĩa Mặt Cầu
Mặt cầu là tập hợp tất cả các điểm trong không gian cách một điểm cố định (gọi là tâm) một khoảng không đổi (gọi là bán kính).
2. Phương Trình Mặt Cầu
Phương trình mặt cầu với tâm I(a; b; c) và bán kính R được biểu diễn như sau:
(x - a)² + (y - b)² + (z - c)² = R²
3. Các Dạng Phương Trình Mặt Cầu
- Phương trình chính tắc: (x - a)² + (y - b)² + (z - c)² = R²
- Phương trình tổng quát: x² + y² + z² - 2ax - 2by - 2cz + d = 0 (với a² + b² + c² - d > 0 và R = √(a² + b² + c² - d))
4. Điều Kiện Để Phương Trình Là Phương Trình Mặt Cầu
Phương trình x² + y² + z² - 2ax - 2by - 2cz + d = 0 là phương trình của một mặt cầu khi và chỉ khi:
a² + b² + c² - d > 0
5. Các Bài Toán Liên Quan Đến Phương Trình Mặt Cầu
5.1. Xác Định Tâm và Bán Kính Mặt Cầu
Cho phương trình mặt cầu, hãy xác định tọa độ tâm I(a; b; c) và bán kính R.
Ví dụ: Xác định tâm và bán kính của mặt cầu có phương trình (x - 1)² + (y + 2)² + (z - 3)² = 4
Giải: Tâm I(1; -2; 3) và bán kính R = √4 = 2
5.2. Viết Phương Trình Mặt Cầu Khi Biết Tâm và Bán Kính
Cho tọa độ tâm I(a; b; c) và bán kính R, hãy viết phương trình mặt cầu.
Ví dụ: Viết phương trình mặt cầu có tâm I(0; 0; 0) và bán kính R = 5
Giải: Phương trình mặt cầu là x² + y² + z² = 25
5.3. Xác Định Xem Một Điểm Có Nằm Trên Mặt Cầu Hay Không
Cho phương trình mặt cầu và tọa độ một điểm, hãy xác định xem điểm đó có nằm trên mặt cầu hay không.
Cách làm: Thay tọa độ điểm vào phương trình mặt cầu. Nếu phương trình thỏa mãn, điểm nằm trên mặt cầu. Ngược lại, điểm không nằm trên mặt cầu.
6. Bài Tập Vận Dụng
- Viết phương trình mặt cầu có tâm I(2; -1; 3) và bán kính R = 4.
- Xác định tâm và bán kính của mặt cầu có phương trình x² + y² + z² + 2x - 4y + 6z - 11 = 0.
- Điểm A(1; 2; 3) có nằm trên mặt cầu (x - 1)² + (y - 2)² + (z - 3)² = 1 hay không?
7. Lời Khuyên Khi Học Lý Thuyết Phương Trình Mặt Cầu
- Nắm vững định nghĩa và các dạng phương trình mặt cầu.
- Luyện tập thường xuyên các bài tập để hiểu rõ cách áp dụng lý thuyết vào giải bài toán.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi hoặc phần mềm vẽ hình để kiểm tra kết quả.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Phương trình mặt cầu Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt!