Giải bài tập 6 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tusach.vn xin giới thiệu lời giải chi tiết bài tập 6 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo. Bài viết này sẽ giúp học sinh hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chính xác, dễ hiểu và cập nhật mới nhất để hỗ trợ tốt nhất cho quá trình học tập của bạn.
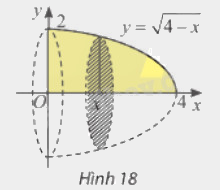
Cho (D) là hình phẳng giới hạn bởi đồ thị hàm số (y = sqrt {4 - x} ) (left( {x le 4} right)), trục tung và trục hoành (hình dưới đây). Tính thể tích khối tròn xoay tạo thành khi quay (D) quanh trục (Ox).
Giải bài tập 6 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 6 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào chủ đề về Đạo hàm của hàm số hợp. Đây là một phần kiến thức quan trọng, thường xuyên xuất hiện trong các bài kiểm tra và kỳ thi THPT Quốc gia. Việc nắm vững phương pháp giải các bài tập liên quan đến đạo hàm hàm hợp là điều cần thiết để đạt kết quả tốt môn Toán.
Nội dung bài tập 6 trang 27 SGK Toán 12 tập 2 - Chân trời sáng tạo
Bài tập 6 yêu cầu học sinh tính đạo hàm của các hàm số được cho. Các hàm số này thường có dạng hợp, tức là một hàm số được tạo thành từ việc ghép nhiều hàm số đơn giản lại với nhau. Để giải bài tập này, học sinh cần áp dụng quy tắc đạo hàm của hàm hợp:
(u(v(x)))' = u'(v(x)) * v'(x)
Trong đó:
- u(v(x)) là hàm số hợp.
- u'(v(x)) là đạo hàm của hàm u theo v.
- v'(x) là đạo hàm của hàm v theo x.
Ví dụ minh họa và lời giải chi tiết
Ví dụ 1: Tính đạo hàm của hàm số y = sin(x2 + 1)
Lời giải:
- Đặt u = x2 + 1 và v = u.
- Khi đó, y = sin(u).
- Tính đạo hàm của u và y theo x:
- Áp dụng quy tắc đạo hàm hàm hợp:
- y' = cos(x2 + 1) * 2x = 2x * cos(x2 + 1)
Ví dụ 2: Tính đạo hàm của hàm số y = ecos(x)
Lời giải:
- Đặt u = cos(x) và v = u.
- Khi đó, y = eu.
- Tính đạo hàm của u và y theo x:
- Áp dụng quy tắc đạo hàm hàm hợp:
- y' = ecos(x) * (-sin(x)) = -sin(x) * ecos(x)
Mẹo giải bài tập đạo hàm hàm hợp
- Xác định rõ hàm số bên trong (v(x)) và hàm số bên ngoài (u(x)).
- Tính đạo hàm của từng hàm số một cách chính xác.
- Áp dụng quy tắc đạo hàm hàm hợp một cách cẩn thận.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
Bài tập tương tự để luyện tập
Để củng cố kiến thức và kỹ năng giải bài tập đạo hàm hàm hợp, bạn có thể luyện tập thêm với các bài tập tương tự sau:
- Tính đạo hàm của hàm số y = tan(2x + 1)
- Tính đạo hàm của hàm số y = ln(sin(x))
- Tính đạo hàm của hàm số y = (x2 + 1)3
Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn là một website cung cấp đầy đủ các tài liệu học tập Toán 12, bao gồm SGK, SBT, đề thi, bài giải và các bài viết hướng dẫn giải bài tập chi tiết. Chúng tôi luôn cập nhật nội dung mới nhất và đảm bảo tính chính xác, dễ hiểu để hỗ trợ tốt nhất cho quá trình học tập của bạn. Hãy truy cập Tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!