Giải mục 3 trang 28,29,30 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải Mục 3 Trang 28,29,30 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo
Chào mừng các em học sinh đến với lời giải chi tiết Mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 Chân trời sáng tạo. Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Mục tiêu của chúng tôi là giúp các em nắm vững kiến thức, tự tin giải quyết các bài tập Toán 12 và đạt kết quả cao trong các kỳ thi.
Khảo sát hàm số \(y = \frac{{ax + b}}{{cx + d}}(c \ne 0,ad - bc \ne 0)\)
TH2
Trả lời câu hỏi Thực hành 2 trang 30 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{2x}}{{3x - 1}}\)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm các tiệm cận của đồ thị hàm số
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
- Chiều biến thiên:
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} \le 0\forall x \in D\)nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1\) nên y = 1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
Bảng biến thiên: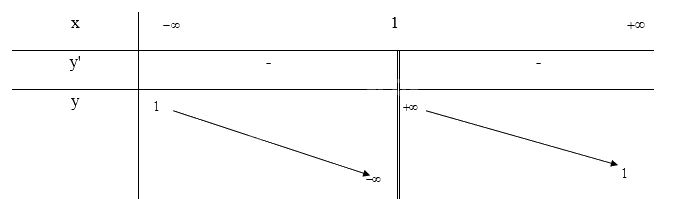
Khi x = 0 thì y = -1 nên (0; -1) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{x + 1}}{{x - 1}} = 0 \Leftrightarrow x = - 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1; 0)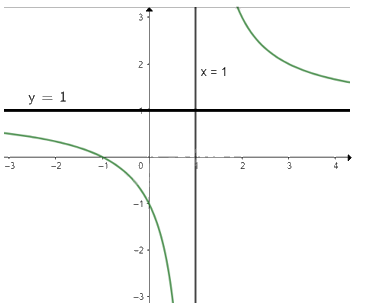
b) \(y = \frac{{2x}}{{3x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{3}\} \)
- Chiều biến thiên:
\(y' = \frac{{ - 2}}{{{{(3x - 1)}^2}}} \le 0\forall x \in D\) nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3};\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3}\) nên y = \(\frac{2}{3}\) là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} \frac{{2x}}{{3x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} \frac{{2x}}{{3x - 1}} = - \infty \) nên x = \(\frac{1}{3}\) là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
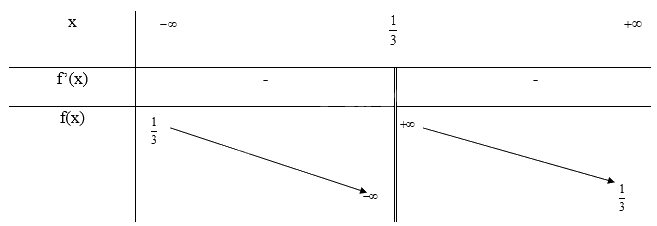
Khi x = 0 thì y = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{2x}}{{3x - 1}} = 0 \Leftrightarrow x = 0\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (0; 0)
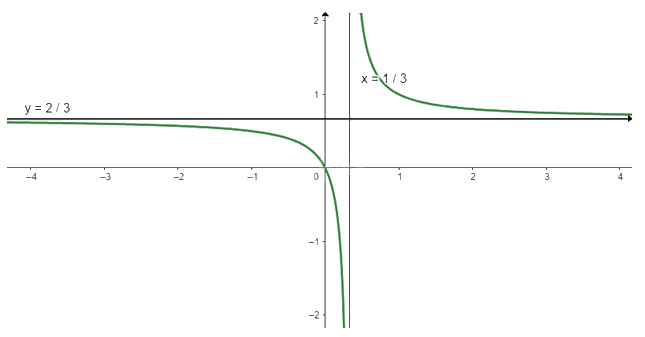
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
- Chiều biến thiên:
\(y' = \frac{7}{{{{(2 - x)}^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 + x}}{{2 - x}} = - 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 + x}}{{2 - x}} = - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} y = \frac{{5 + x}}{{2 - x}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x}}{{3x - 1}} = + \infty \) nên x = 2 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
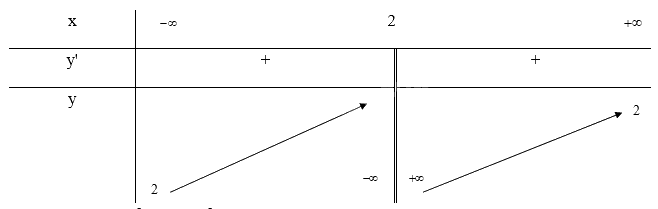
Khi x = 0 thì y = \(\frac{5}{2}\) nên (0; \(\frac{5}{2}\)) là giao điểm của đồ thị với trục Oy
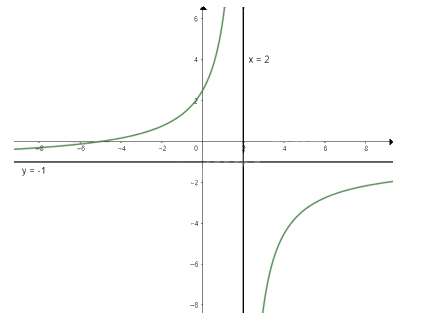
Ta có: \(y = 0 \Leftrightarrow \frac{{5 + x}}{{2 - x}} = 0 \Leftrightarrow x = - 5\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-5; 0)
- TH2
Trả lời câu hỏi Thực hành 2 trang 30 SGK Toán 12 Chân trời sáng tạo
Khảo sát và vẽ đồ thị của các hàm số sau:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
b) \(y = \frac{{2x}}{{3x - 1}}\)
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Phương pháp giải:
Bước 1. Tìm tập xác định của hàm số
Bước 2. Xét sự biến thiên của hàm số
− Tìm đạo hàm y', xét dấu y', xác định khoảng đơn điệu của hàm số.
− Tìm các tiệm cận của đồ thị hàm số
− Lập bảng biến thiên của hàm số.
Bước 3. Vẽ đồ thị của hàm số
− Xác định các giao điểm của đồ thị với các trục toạ độ
− Vẽ các đường tiệm cận của đồ thị hàm số (nếu có).
− Vẽ đồ thị hàm số.
Lời giải chi tiết:
a) \(y = \frac{{x + 1}}{{x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 1\} \)
- Chiều biến thiên:
\(y' = \frac{{ - 2}}{{{{(x - 1)}^2}}} \le 0\forall x \in D\)nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{x + 1}}{{x - 1}} = 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{x + 1}}{{x - 1}} = 1\) nên y = 1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \frac{{x + 1}}{{x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \frac{{x + 1}}{{x - 1}} = - \infty \) nên x = 1 là tiệm cận đứng của đồ thị hàm số
Bảng biến thiên: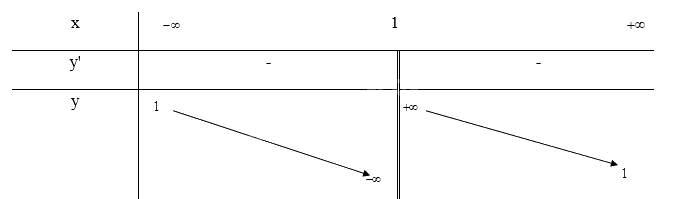
Khi x = 0 thì y = -1 nên (0; -1) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{x + 1}}{{x - 1}} = 0 \Leftrightarrow x = - 1\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-1; 0)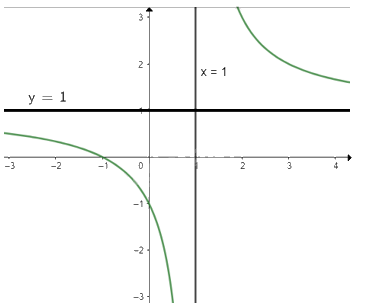
b) \(y = \frac{{2x}}{{3x - 1}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ \frac{1}{3}\} \)
- Chiều biến thiên:
\(y' = \frac{{ - 2}}{{{{(3x - 1)}^2}}} \le 0\forall x \in D\) nên hàm số nghịch biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3};\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{2x}}{{3x - 1}} = \frac{2}{3}\) nên y = \(\frac{2}{3}\) là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ + }} \frac{{2x}}{{3x - 1}} = + \infty ;\mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} y = \mathop {\lim }\limits_{x \to {{\frac{1}{3}}^ - }} \frac{{2x}}{{3x - 1}} = - \infty \) nên x = \(\frac{1}{3}\) là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
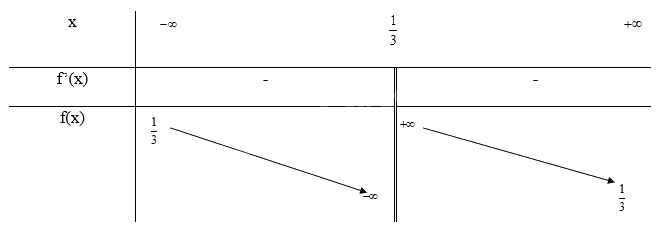
Khi x = 0 thì y = 0 nên (0; 0) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{2x}}{{3x - 1}} = 0 \Leftrightarrow x = 0\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (0; 0)
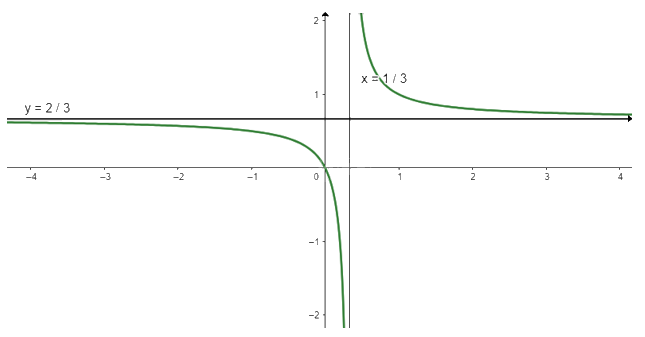
c) \(y = \frac{{5 + x}}{{2 - x}}\)
Tập xác định: \(D = \mathbb{R}\backslash \{ 2\} \)
- Chiều biến thiên:
\(y' = \frac{7}{{{{(2 - x)}^2}}} \ge 0\forall x \in D\) nên hàm số đồng biến trên D
- Tiệm cận:
\(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \frac{{5 + x}}{{2 - x}} = - 1;\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \frac{{5 + x}}{{2 - x}} = - 1\) nên y = -1 là tiệm cận ngang của đồ thị hàm số
\(\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} y = \frac{{5 + x}}{{2 - x}} = - \infty ;\mathop {\lim }\limits_{x \to {2^ - }} y = \mathop {\lim }\limits_{x \to {2^ - }} \frac{{2x}}{{3x - 1}} = + \infty \) nên x = 2 là tiệm cận đứng của đồ thị hàm số
- Bảng biến thiên:
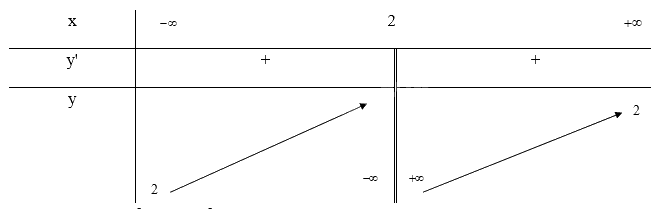
Khi x = 0 thì y = \(\frac{5}{2}\) nên (0; \(\frac{5}{2}\)) là giao điểm của đồ thị với trục Oy
Ta có: \(y = 0 \Leftrightarrow \frac{{5 + x}}{{2 - x}} = 0 \Leftrightarrow x = - 5\)
Vậy đồ thị của hàm số giao với trục Ox tại điểm (-5; 0)
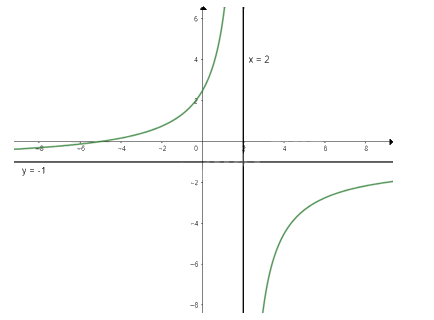
Giải Mục 3 Trang 28,29,30 SGK Toán 12 Tập 1 - Chân Trời Sáng Tạo: Tổng Quan và Phương Pháp Giải
Mục 3 trong SGK Toán 12 tập 1 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết hiệu quả các bài tập trong mục này, học sinh cần nắm vững kiến thức lý thuyết, hiểu rõ các định nghĩa, định lý và công thức liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết cho từng bài tập, đồng thời phân tích phương pháp giải để các em hiểu rõ bản chất vấn đề.
Nội Dung Chính của Mục 3 (Trang 28, 29, 30)
Thông thường, Mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 Chân trời sáng tạo sẽ bao gồm các dạng bài tập sau:
- Bài tập vận dụng kiến thức lý thuyết: Kiểm tra khả năng hiểu và áp dụng các khái niệm đã học.
- Bài tập tính toán: Yêu cầu thực hiện các phép tính toán dựa trên công thức và định lý.
- Bài tập chứng minh: Đòi hỏi học sinh phải trình bày một cách logic và chặt chẽ để chứng minh một khẳng định nào đó.
- Bài tập thực tế: Liên hệ kiến thức Toán học với các tình huống thực tế, giúp học sinh hiểu rõ hơn về ứng dụng của môn học.
Lời Giải Chi Tiết Các Bài Tập
Dưới đây là lời giải chi tiết cho từng bài tập trong Mục 3 trang 28, 29, 30 SGK Toán 12 tập 1 Chân trời sáng tạo:
Bài 1: (Trang 28)
(Nội dung bài tập và lời giải chi tiết)
Bài 2: (Trang 29)
(Nội dung bài tập và lời giải chi tiết)
Bài 3: (Trang 30)
(Nội dung bài tập và lời giải chi tiết)
Phương Pháp Giải Toán 12 Hiệu Quả
Để học Toán 12 hiệu quả, các em cần:
- Nắm vững kiến thức lý thuyết: Đọc kỹ SGK, ghi chép đầy đủ và hệ thống hóa kiến thức.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài.
- Tìm kiếm sự giúp đỡ khi cần thiết: Hỏi thầy cô, bạn bè hoặc tham khảo các nguồn tài liệu trực tuyến.
- Sử dụng các công cụ hỗ trợ: Máy tính bỏ túi, phần mềm giải toán, các trang web học Toán trực tuyến.
Bảng Tổng Hợp Công Thức Quan Trọng
| Công Thức | Mô Tả |
|---|---|
| (Công thức 1) | (Mô tả công thức 1) |
| (Công thức 2) | (Mô tả công thức 2) |
Tusach.vn hy vọng rằng với lời giải chi tiết và phương pháp giải hiệu quả này, các em sẽ tự tin hơn trong việc học Toán 12. Chúc các em học tập tốt!
Lưu ý: Nội dung bài giải có thể thay đổi tùy theo phiên bản SGK. Các em vui lòng đối chiếu với SGK của mình để đảm bảo tính chính xác.