Lựa chọn câu để xem lời giải nhanh hơnTrả lời câu hỏi Khám phá 5 trang 48 SGK Toán 12 Chân trời sáng tạo
a) Nhắc lại định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng.
b) Làm thế nào để định nghĩa góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian?
Phương pháp giải:
Nhớ lại định nghĩa đã học về góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong mặt phẳng và suy luận ra góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) trong không gian.
Lời giải chi tiết:
a) Trong mặt phẳng, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Trả lời câu hỏi Thực hành 8 trang 48 SGK Toán 12 Chân trời sáng tạo
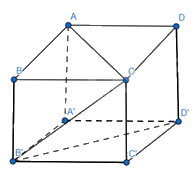
Cho hình lập phương ABCD.A′B′C′D′. Xác định góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} ),(\overrightarrow {A'A} ,\overrightarrow {CB'} )\)
Phương pháp giải:
Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
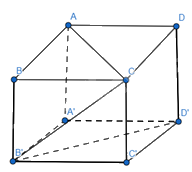
Góc \((\overrightarrow {AC} ,\overrightarrow {B'D'} )\) = góc \((\overrightarrow {AC} ,\overrightarrow {BD} )\) = \(90^\circ \) (góc giữa 2 đường chéo của hình vuông)
\((\overrightarrow {A'A} ,\overrightarrow {CB'} ) = (\overrightarrow {B'B} ,\overrightarrow {CB'} ) = {180^o} - (\overrightarrow {B'B} ,\overrightarrow {B'C} ) = {180^o} - {45^o} = {135^o}\)
Trả lời câu hỏi Khám phá 6 trang 49 SGK Toán 12 Chân trời sáng tạo
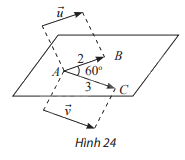
Trong không gian, cho \(\overrightarrow u \) và \(\overrightarrow v \) thoả mãn \(|\overrightarrow u | = 2\) , \(|\overrightarrow v | = 3\). Lấy một điểm A bất kì, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \), \(\overrightarrow {AC} = \overrightarrow v \) (Hình 24). Giả sử \(\widehat {BAC} = 60^\circ \)
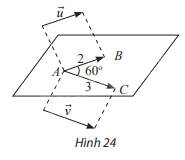
a) Tính góc \((\overrightarrow u ,\overrightarrow v )\)
b) Trong mặt phẳng (ABC), tính tích vô hướng \(\overrightarrow {AB} .\overrightarrow {AC} \)
Phương pháp giải:
a) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
b) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
Lời giải chi tiết:
a) Góc \((\overrightarrow u ,\overrightarrow v )\) = \(\widehat {BAC} = 60^\circ \)
b) \(\overrightarrow {AB} .\overrightarrow {AC} \) = \(AB.AC.\cos \widehat {BAC} = 2.3.\cos 60^\circ = 3\)
Trả lời câu hỏi Thực hành 9 trang 50 SGK Toán 12 Chân trời sáng tạo
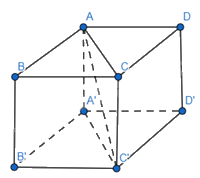
Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1.
a) Tính các tích vô hướng: \(\overrightarrow {AB} .\overrightarrow {A'C'} \), \(\overrightarrow {AB} .\overrightarrow {CC'} \)
b) Tính góc \((\overrightarrow {AC} .\overrightarrow {AC'} )\) (kết quả làm tròn đến phút).
Phương pháp giải:
a) Công thức tính tích vô hướng của 2 vecto: \(\overrightarrow u .\overrightarrow v = |\overrightarrow u |.|\overrightarrow v |.\cos (\overrightarrow u ,\overrightarrow v )\)
b) Trong không gian, cho hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \) đều khác vectơ không. Từ một điểm A bất kỳ, gọi B và C là hai điểm sao cho \(\overrightarrow {AB} = \overrightarrow u \) và \(\overrightarrow {AC} = \overrightarrow v \). Khi đó góc \(\widehat {BAC}\) được gọi là góc giữa hai vectơ \(\overrightarrow u \) và \(\overrightarrow v \).
Lời giải chi tiết:
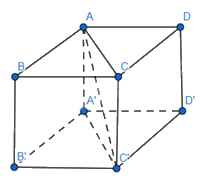
a) \(\overrightarrow {AB} .\overrightarrow {A'C'} = \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\cos \widehat {BAC} = 1.\sqrt 2 .\cos 45^\circ = 1\)
\(\overrightarrow {AB} .\overrightarrow {CC'} = \overrightarrow {AB} .\overrightarrow {BB'} = 0\) vì \(\overrightarrow {AB} \bot \overrightarrow {BB'} \)
b) Xét tam giác CAC’ vuông tại C:
\(AC = \sqrt 2 \); CC’ = 1 => \(\tan (\overrightarrow {AC} ,\overrightarrow {AC'} ) = \tan \widehat {C'AC} = \frac{{CC'}}{{AC}} = \frac{1}{{\sqrt 2 }} \Rightarrow \widehat {C'AC} = 35^\circ \).
Trả lời câu hỏi Vận dụng 4 trang 50 SGK Toán 12 Chân trời sáng tạo
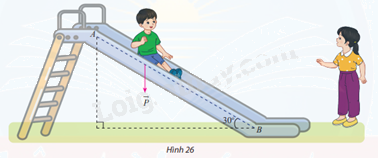
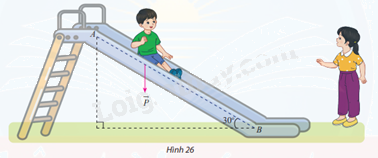
Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5m. Biết rằng, cầu trượt có góc nghiêng so với phương nằm ngang là \(30^\circ \) (Hình 26).
a) Tính độ lớn của trọng lực \(\overrightarrow P = m\overrightarrow g \) tác dụng lên em nhỏ, cho biết vectơ gia tốc rơi tự do \(\overrightarrow g \) có độ lớn 9,8\(m/{s^2}\)
b) Cho biết công A (J) sinh bởi một lực \(\overrightarrow F \) có độ dịch chuyển \(\overrightarrow d \) được tính bởi công thức \(A = \overrightarrow F .\overrightarrow d \). Hãy tính công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt.
Phương pháp giải:
a) Áp dụng công thức tính trọng lực P = mg
b) Công thức tính công: \(A = Fs\cos \alpha \)
Lời giải chi tiết:
a) Độ lớn trọng lực tác dụng lên em nhỏ là: \(P = mg = 25.9,8 = 245N\)
b) Công sinh bởi trọng lực \(\overrightarrow P \) khi em nhỏ trượt hết chiều dài cầu trượt là: \(A = \overrightarrow F .\overrightarrow d = Pd\cos 60^\circ = 245.3,5.\frac{1}{2} = 428,75J\)