Lý thuyết Ứng dụng hình học của tích phân Toán 12 Chân trời sáng tạo
Tổng quan nội dung
Lý thuyết Ứng dụng hình học của tích phân Toán 12 Chân trời sáng tạo
Chương trình Toán 12 Chân trời sáng tạo, phần Ứng dụng hình học của tích phân đóng vai trò quan trọng trong việc củng cố kiến thức và rèn luyện kỹ năng giải quyết các bài toán thực tế. Phần này tập trung vào việc sử dụng tích phân để tính diện tích hình phẳng và thể tích khối tròn xoay.
Tusach.vn cung cấp tài liệu học tập đầy đủ, chi tiết, giúp học sinh nắm vững lý thuyết và phương pháp giải bài tập một cách hiệu quả.
1.Tính diện tích hình phẳng a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b
1.Tính diện tích hình phẳng
a) Diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y = f(x) liên tục, trục hoành và hai đường thẳng x = a, x = b (a < b) được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x)} \right|dx} \) |
Nếu hàm số \(y = f(x)\) không đổi dấu trên đoạn [a;b] thì \(S = \int\limits_a^b {\left| {f(x)} \right|dx} = \left| {\int\limits_a^b {f(x)dx} } \right|\).
Đặc biệt, nếu phương trình \(f(x) = 0\) không có nghiệm trên khoảng (a;b) thì công thức trên vẫn đúng.
Nếu phương trình \(f(x) = 0\) chỉ có một nghiệm c trên khoảng (a;b) thì \(S = \left| {\int\limits_a^c {f(x)dx} } \right| + \left| {\int\limits_c^b {f(x)dx} } \right|\).
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f(x) = {x^2} - 4x + 3\), trục hoành và hai đường thẳng x = 0, x = 3.
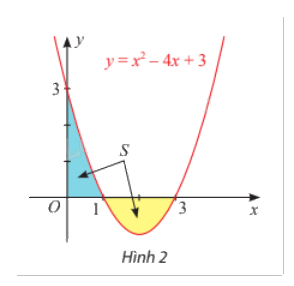
Giải: Diện tích cần tìm là \(S = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx} \).
Ta có: \({x^2} - 4x + 3 = 0 \Leftrightarrow \) x = 1 hoặc x = 3.
Với \(x \in \left[ {0;1} \right]\) thì \(f(x) \ge 0\). Với \(x \in \left[ {1;3} \right]\) thì \(f(x) \le 0\).
Vậy \(S = \int\limits_0^3 {\left| {{x^2} - 4x + 3} \right|dx} = \int\limits_0^1 {\left( {{x^2} - 4x + 3} \right)dx} + \int\limits_1^3 {\left[ { - \left( {{x^2} - 4x + 3} \right)} \right]dx} \)
\( = \left( {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right)\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right. - \left( {\frac{{{x^3}}}{3} - 2{x^2} + 3x} \right)\left| {\begin{array}{*{20}{c}}3\\1\end{array}} \right. = \frac{8}{3}\).
b) Diện tích hình phẳng giới hạn bởi đồ thị các hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b
Diện tích S của hình phẳng giới hạn bởi đồ thị của hai hàm số y = f(x), g(x) liên tục trên \(\left[ {a;b} \right]\) và hai đường thẳng x = a, x = b được tính bằng công thức \(S = \int\limits_a^b {\left| {f(x) - g(x)} \right|dx} \) |
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\), \(y = 2 - x\) và hai đường thẳng x = 0, x = 2.
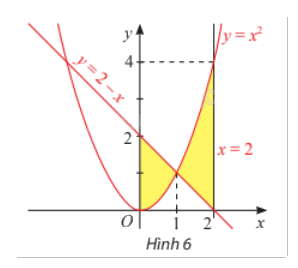
Giải: Diện tích cần tìm là \(\int\limits_0^2 {\left| {{x^2} - (2 - x)} \right|dx} = \int\limits_0^2 {\left| {{x^2} + x - 2} \right|dx} \).
Ta có \({x^2} + x - 2 = 0 \Leftrightarrow \) x = 1 hoặc x = -2.
Vậy \(S = \int\limits_0^1 {\left| {{x^2} + x - 2} \right|dx} + \int\limits_1^2 {\left| {{x^2} + x - 2} \right|dx} = \left| {\int\limits_0^1 {\left( {{x^2} + x - 2} \right)dx} } \right| + \left| {\int\limits_1^2 {\left( {{x^2} + x - 2} \right)dx} } \right|\)
\( = \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}1\\0\end{array}} \right.} \right| + \left| {\left( {\frac{{{x^3}}}{3} + \frac{{{x^2}}}{2} - 2x} \right)\left| {\begin{array}{*{20}{c}}2\\1\end{array}} \right.} \right| = \left| { - \frac{7}{6}} \right| + \left| {\frac{{11}}{6}} \right| = 3\).
2. Tính thể tích của hình khối
Cho một vật thể trong không gian giữa hai mặt phẳng (P) và (Q) cùng vuông góc với trục Ox tại các điểm a và b. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ là x \((a \le x \le b)\) cắt vật thể theo mặt cắt có diện tích là S(x), với S(x) là hàm số liên tục. Thể tích của vật thể được tính bằng công thức \(V = \int\limits_a^b {S(x)dx} \) |
Ví dụ: Cho khối lăng trụ tam giác có diện tích đáy S và chiều cao h. Sử dụng tích phân, tính thể tích của khối lăng trụ theo S và h.
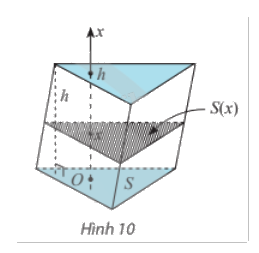
Giải: Chọn trục Ox song song với đường cao của khối lăng trụ sao cho hai đáy nằm trong hai mặt phẳng vuông góc với Ox tại x = 0 và x = h.
Mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x \((0 \le x \le h)\) cắt lăng trụ theo mặt cắt có diện tích không đổi S(x) = S. Do đó, thể tích khối lăng trụ là \(V = \int\limits_0^h {S(x)dx} = \int\limits_0^h {Sdx} = Sx\left| {\begin{array}{*{20}{c}}h\\0\end{array}} \right. = Sh\).
3. Thể tích khối tròn xoay
Cho \(y = f(x)\) là hàm số liên tục và không âm trên đoạn [a;b]. Gọi D là hình phẳng giới hạn bởi đồ thị hàm số \(y = f(x)\), trục hoành và hai đường thẳng x = a, x = b.
Quay D quanh trục Ox ta được một hình khối gọi là khối tròn xoay.
Cắt khối tròn xoay trên bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x với \(x \in [a;b]\), ta được mặt cắt là hình tròn có bán kính bằng \(f(x)\) và diện tích là \(S(x) = \pi {f^2}(x)\).
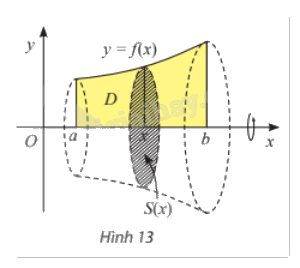
Cho hình phẳng D được giới hạn bởi đồ thị của hàm số \(y = f(x)\) liên tục trên đoạn [a;b], trục Ox và hai đường thẳng x = a, y = b. Quay D quanh trục Ox, ta được khối tròn xoay có thể tích được tính bằng công thức \(V = \pi \int\limits_a^b {{f^2}(x)dx} \)\(\) |
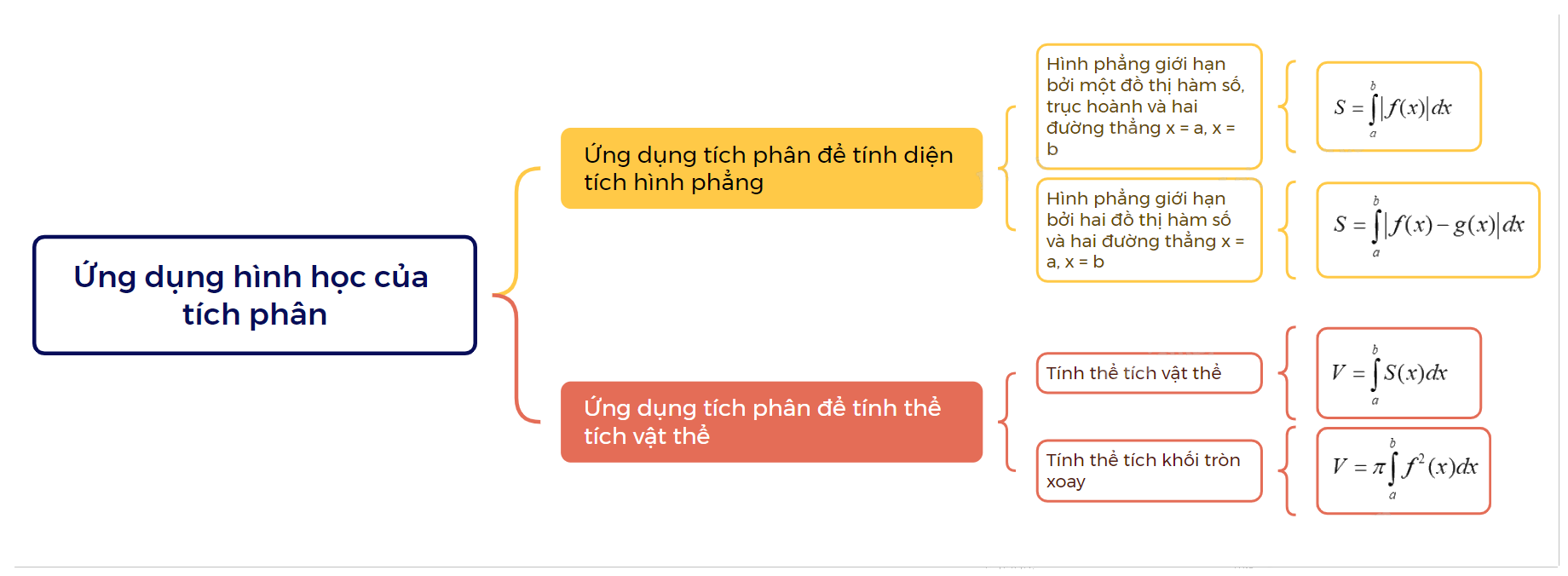
Lý Thuyết Ứng Dụng Hình Học Tích Phân Toán 12 Chân Trời Sáng Tạo: Tổng Quan và Hướng Dẫn Chi Tiết
Ứng dụng hình học của tích phân là một trong những nội dung trọng tâm của chương trình Toán 12 Chân trời sáng tạo. Nó không chỉ giúp học sinh hiểu sâu hơn về tích phân mà còn rèn luyện khả năng tư duy logic và giải quyết vấn đề. Bài viết này sẽ cung cấp một cái nhìn tổng quan và hướng dẫn chi tiết về phần lý thuyết này.
1. Giới Thiệu Chung về Ứng Dụng Hình Học của Tích Phân
Tích phân, một trong hai phép toán cơ bản của giải tích (cùng với đạo hàm), có ứng dụng rộng rãi trong nhiều lĩnh vực khoa học và kỹ thuật. Trong hình học, tích phân được sử dụng để tính diện tích của các hình phẳng phức tạp và thể tích của các khối tròn xoay. Việc hiểu rõ nguyên lý và phương pháp tính toán là điều cần thiết để giải quyết các bài toán liên quan.
2. Tính Diện Tích Hình Phẳng
Để tính diện tích hình phẳng giới hạn bởi đường cong y = f(x), trục Ox và hai đường thẳng x = a, x = b, ta sử dụng công thức:
Diện tích = ∫ab |f(x)| dx
Trong đó:
- f(x) là hàm số xác định trên đoạn [a, b]
- |f(x)| là giá trị tuyệt đối của f(x)
Ví dụ: Tính diện tích hình phẳng giới hạn bởi đường cong y = x2, trục Ox và hai đường thẳng x = 0, x = 2.
Giải:
Diện tích = ∫02 x2 dx = [x3/3]02 = 8/3
3. Tính Thể Tích Khối Tròn Xoay
Có hai phương pháp chính để tính thể tích khối tròn xoay:
- Phương pháp đĩa: Sử dụng khi quay quanh trục Ox hoặc Oy.
- Phương pháp vỏ: Sử dụng khi quay quanh trục Ox hoặc Oy.
a. Phương pháp đĩa:
Nếu quay hình phẳng giới hạn bởi y = f(x), trục Ox và hai đường thẳng x = a, x = b quanh trục Ox, thể tích khối tròn xoay được tính bằng:
Thể tích = π ∫ab [f(x)]2 dx
b. Phương pháp vỏ:
Nếu quay hình phẳng giới hạn bởi y = f(x), trục Oy và hai đường thẳng y = c, y = d quanh trục Oy, thể tích khối tròn xoay được tính bằng:
Thể tích = 2π ∫cd x * f(x) dx
4. Các Dạng Bài Tập Thường Gặp
Các bài tập về ứng dụng hình học của tích phân thường xoay quanh các chủ đề sau:
- Tính diện tích hình phẳng giới hạn bởi các đường cong.
- Tính thể tích khối tròn xoay tạo bởi việc quay một hình phẳng quanh một trục.
- Ứng dụng tích phân để giải các bài toán thực tế liên quan đến diện tích và thể tích.
5. Mẹo Giải Bài Tập Hiệu Quả
Để giải các bài tập về ứng dụng hình học của tích phân một cách hiệu quả, bạn nên:
- Vẽ hình minh họa để hình dung rõ ràng bài toán.
- Xác định chính xác giới hạn tích phân.
- Chọn phương pháp tích phân phù hợp (phương pháp đĩa hoặc phương pháp vỏ).
- Kiểm tra lại kết quả sau khi tính toán.
6. Tài Liệu Tham Khảo và Luyện Tập
Để nắm vững kiến thức và rèn luyện kỹ năng, bạn có thể tham khảo:
- Sách giáo khoa Toán 12 Chân trời sáng tạo.
- Các bài giảng trực tuyến trên Tusach.vn.
- Các bài tập luyện tập có đáp án.
Hy vọng bài viết này đã cung cấp cho bạn những kiến thức hữu ích về Lý thuyết Ứng dụng hình học của tích phân Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt!