Logo

Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo

Tổng quan nội dung

Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 6 trang 57 SGK Toán 12 tập 1 thuộc chương trình học môn Toán lớp 12, tập trung vào chủ đề về giới hạn của hàm số. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để tính toán và chứng minh các giới hạn, đồng thời rèn luyện kỹ năng giải toán.

Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.

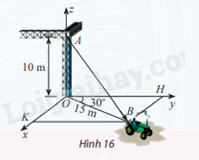
Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ Oxyz như Hình 16 với độ dài đơn vị trên các trục toạ độ bằng 1 m. Tìm toạ độ của vectơ \(\overrightarrow {AB} \)

Đề bài

Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập hệ toạ độ Oxyz như Hình 16 với độ dài đơn vị trên các trục toạ độ bằng 1 m. Tìm toạ độ của vectơ \(\overrightarrow {AB} \)

Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiếtGiải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo 2

Quan sát hình vẽ. Tìm tọa độ điểm A, B rồi tính tọa độ vectơ \(\overrightarrow {AB} \)

Lời giải chi tiết

\(\overrightarrow {OA} = 10\overrightarrow k = > A(0;0;10)\)

Ta có: \(OH = OB.\cos 30^\circ = \frac{{15\sqrt 3 }}{2}\)

\(OK = OB.\cos (90^\circ - 30^\circ ) = \frac{{15}}{2}\)

Vậy B(\(\frac{{15}}{2}\);\(\frac{{15\sqrt 3 }}{2}\);0)

=> \(\overrightarrow {AB} = (\frac{{15}}{2};\frac{{15\sqrt 3 }}{2}; - 10)\)

Giải bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu

Bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo là một bài tập quan trọng trong chương trình học môn Toán lớp 12, tập trung vào việc vận dụng kiến thức về giới hạn của hàm số. Để giúp các em học sinh hiểu rõ hơn về bài tập này, Tusach.vn xin giới thiệu hướng dẫn giải chi tiết và dễ hiểu sau đây.

Nội dung bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo

Bài tập 6 yêu cầu tính các giới hạn sau:

  1. limx→2 (x2 - 3x + 2) / (x - 2)
  2. limx→-1 (x3 + 1) / (x + 1)
  3. limx→0 (√(x+1) - 1) / x

Hướng dẫn giải chi tiết

Để giải các bài tập về giới hạn, chúng ta cần nắm vững các phương pháp sau:

  • Phương pháp đặt nhân tử chung: Sử dụng khi biểu thức có dạng phân thức và tử thức có thể phân tích thành nhân tử chứa mẫu thức.
  • Phương pháp nhân liên hợp: Sử dụng khi biểu thức chứa căn thức.
  • Quy tắc giới hạn: Áp dụng các quy tắc về giới hạn của tổng, hiệu, tích, thương và lũy thừa.
Giải bài tập 6.1: limx→2 (x2 - 3x + 2) / (x - 2)

Ta có: x2 - 3x + 2 = (x - 1)(x - 2). Do đó:

limx→2 (x2 - 3x + 2) / (x - 2) = limx→2 (x - 1)(x - 2) / (x - 2) = limx→2 (x - 1) = 2 - 1 = 1

Giải bài tập 6.2: limx→-1 (x3 + 1) / (x + 1)

Ta có: x3 + 1 = (x + 1)(x2 - x + 1). Do đó:

limx→-1 (x3 + 1) / (x + 1) = limx→-1 (x + 1)(x2 - x + 1) / (x + 1) = limx→-1 (x2 - x + 1) = (-1)2 - (-1) + 1 = 1 + 1 + 1 = 3

Giải bài tập 6.3: limx→0 (√(x+1) - 1) / x

Để giải bài này, ta nhân cả tử và mẫu với liên hợp của tử thức là √(x+1) + 1:

limx→0 (√(x+1) - 1) / x = limx→0 [(√(x+1) - 1)(√(x+1) + 1)] / [x(√(x+1) + 1)] = limx→0 (x+1 - 1) / [x(√(x+1) + 1)] = limx→0 x / [x(√(x+1) + 1)] = limx→0 1 / (√(x+1) + 1) = 1 / (√(0+1) + 1) = 1 / (1 + 1) = 1/2

Kết luận

Vậy, kết quả của các giới hạn là:

  • limx→2 (x2 - 3x + 2) / (x - 2) = 1
  • limx→-1 (x3 + 1) / (x + 1) = 3
  • limx→0 (√(x+1) - 1) / x = 1/2

Hy vọng hướng dẫn giải chi tiết này sẽ giúp các em học sinh hiểu rõ hơn về bài tập 6 trang 57 SGK Toán 12 tập 1 - Chân trời sáng tạo và tự tin làm bài tập. Nếu có bất kỳ thắc mắc nào, hãy liên hệ với Tusach.vn để được hỗ trợ.