Giải bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải Bài Tập 1 Trang 13 Toán 12 Tập 1 - Chân Trời Sáng Tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo. Bài viết này được tusach.vn biên soạn nhằm hỗ trợ các em trong quá trình học tập và ôn luyện môn Toán.
Chúng tôi sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em hiểu sâu sắc kiến thức và tự tin giải quyết các bài tập tương tự.
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
Đề bài
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.
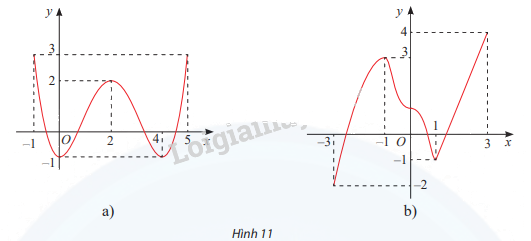
Phương pháp giải - Xem chi tiết
Quan sát đồ thị
Lời giải chi tiết
a) Hàm số đồng biến trên khoảng (0;2) và (4;5), nghịch biến trên khoảng (-1;0) và (2;4)
Hàm số đạt cực đại tại x = 2, \({y_{cd}} = f(2) = 2\), đạt cực tiểu tại x = 0, \({y_{ct}} = f(0) = - 1\) và x = 4, \({y_{ct}} = f(4) = - 1\)
b) Hàm số đồng biến trên khoảng (-3;-1) và (1;3), nghịch biến trên khoảng (-1;1)
Hàm số đạt cực đại tại x = -1, \({y_{cd}} = f( - 1) = 3\), đạt cực tiểu tại x = 1, \({y_{ct}} = f(1) = - 1\)
Giải Bài Tập 1 Trang 13 Toán 12 Tập 1 - Chân Trời Sáng Tạo: Hướng Dẫn Chi Tiết
Bài tập 1 trang 13 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học môn Toán lớp 12, tập trung vào việc ôn tập kiến thức về hàm số và đồ thị. Đây là một bài tập quan trọng giúp học sinh củng cố lý thuyết và rèn luyện kỹ năng giải toán.
Nội Dung Bài Tập 1
Bài tập 1 yêu cầu học sinh thực hiện các nhiệm vụ sau:
- Xác định tập xác định của hàm số.
- Tìm tập giá trị của hàm số.
- Xác định tính đơn điệu của hàm số.
- Vẽ đồ thị của hàm số.
Lời Giải Chi Tiết Bài Tập 1a
Đề bài: Xét hàm số y = f(x) = 2x + 1. Tìm tập xác định và tập giá trị của hàm số.
Lời giải:
- Tập xác định: Hàm số y = 2x + 1 là hàm số bậc nhất, xác định với mọi giá trị của x. Vậy tập xác định của hàm số là D = ℝ.
- Tập giá trị: Vì hàm số y = 2x + 1 là hàm số bậc nhất với hệ số a = 2 > 0, hàm số đồng biến trên ℝ. Do đó, tập giá trị của hàm số là ℝ.
Lời Giải Chi Tiết Bài Tập 1b
Đề bài: Xét hàm số y = f(x) = x2 - 4x + 3. Tìm tập xác định và tập giá trị của hàm số.
Lời giải:
- Tập xác định: Hàm số y = x2 - 4x + 3 là hàm số bậc hai, xác định với mọi giá trị của x. Vậy tập xác định của hàm số là D = ℝ.
- Tập giá trị: Hàm số y = x2 - 4x + 3 là hàm số bậc hai có hệ số a = 1 > 0, đạt giá trị nhỏ nhất tại x = -b/2a = 4/2 = 2. Giá trị nhỏ nhất của hàm số là y = 22 - 4*2 + 3 = -1. Do đó, tập giá trị của hàm số là [ -1, +∞ ).
Mẹo Giải Bài Tập Hàm Số
Để giải các bài tập về hàm số một cách hiệu quả, các em cần:
- Nắm vững định nghĩa và các tính chất của các loại hàm số.
- Sử dụng các công thức và phương pháp giải toán phù hợp.
- Rèn luyện kỹ năng vẽ đồ thị hàm số.
- Thực hành giải nhiều bài tập khác nhau để làm quen với các dạng bài tập.
Tầm Quan Trọng Của Việc Giải Bài Tập
Việc giải bài tập là một phần quan trọng trong quá trình học tập môn Toán. Nó giúp các em:
- Củng cố kiến thức lý thuyết.
- Rèn luyện kỹ năng giải toán.
- Nâng cao khả năng tư duy logic và phân tích.
- Chuẩn bị tốt cho các kỳ thi sắp tới.
Tusach.vn - Đồng Hành Cùng Các Em
tusach.vn luôn đồng hành cùng các em trong quá trình học tập. Chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong SGK Toán 12 tập 1 - Chân trời sáng tạo. Hãy truy cập tusach.vn để học Toán 12 hiệu quả hơn!
Nếu có bất kỳ thắc mắc nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.