Giải mục 3 trang 53, 54, 55, 65, 57, 58, 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
Tổng quan nội dung
Giải mục 3 trang 53, 54, 55, 65, 57, 58, 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết mục 3 SGK Toán 12 tập 2 Chân trời sáng tạo.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, cung cấp đáp án chính xác và dễ hiểu nhất.
Hãy cùng khám phá lời giải cho từng bài tập để nắm vững kiến thức và đạt kết quả tốt nhất nhé!
Cho hai đường thẳng \(d\) và \(d'\) có vectơ chỉ phương lần lượt là \(\vec a = \left( {2;1;3} \right)\) và \(\vec a' = \left( {3;2; - 8} \right)\).
TH9
Trả lời câu hỏi Thực hành 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai đường thẳng \(d\) và \(d'\) trong mỗi trường hợp sau:
a) \(d:\frac{{x - 7}}{3} = \frac{y}{5} = \frac{{z - 11}}{4}\) và \(d':\frac{{x - 3}}{2} = \frac{{y + 6}}{5} = \frac{{z - 1}}{{ - 4}}.\)
b) \(d:\frac{{x + 9}}{3} = \frac{{y + 4}}{6} = \frac{{z + 1}}{6}\) và \(d':\left\{ \begin{array}{l}x = 9 - 10t\\y = 7 - 10t\\z = 15 + 5t\end{array} \right.\).
c) \(d:\left\{ \begin{array}{l}x = 23 + 2t\\y = 57 + t\\z = 19 - 5t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 24 + t'\\y = 6 + t'\\z = t'\end{array} \right.\).
Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
a) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;5;4} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {2;5; - 4} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.2 + 5.5 + 4.\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {5^2} + {4^2}} .\sqrt {{2^2} + {5^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{\sqrt {10} }}{{10}}\).
Suy ra \(\left( {d,d'} \right) \approx {71^o}34'\).
b) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;6;6} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( { - 10; - 10;5} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.\left( { - 10} \right) + 6.\left( { - 10} \right) + 6.5} \right|}}{{\sqrt {{3^2} + {6^2} + {6^2}} .\sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2} + {5^2}} }} = \frac{4}{9}\).
Suy ra \(\left( {d,d'} \right) \approx {63^o}37'\).
c) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 5} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {1;1;1} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.1 + 1.1 + \left( { - 5} \right).1} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 5} \right)}^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{\sqrt {10} }}{{15}}\).
Suy ra \(\left( {d,d'} \right) \approx {77^o}50'\).
HĐ8
Trả lời câu hỏi Hoạt động 8 trang 53 SGK Toán 12 Chân trời sáng tạo
Cho hai đường thẳng \(d\) và \(d'\) có vectơ chỉ phương lần lượt là \(\vec a = \left( {2;1;3} \right)\) và \(\vec a' = \left( {3;2; - 8} \right)\).
a) Nhắc lại định nghĩa góc giữa hai đường thẳng \(d\) và \(d'\) trong không gian.
b) Vectơ \(\vec b = \left( { - 2;; - 1; - 3} \right)\) có phải là một vectơ chỉ phương của \(d\) không?
c) Giải thích tại sao ta lại có đẳng thức \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa hai đường thẳng trong không gian đã được học ở các lớp dưới.
b) Kiểm tra xem \(\vec b\) có cùng phương với vectơ \(\vec a\) không.
c) Do góc của hai đường thẳng lớn nhất là 90 độ, còn góc giữa hai vectơ lớn nhất là 180 độ.
d) Từ câu c, rút ra kết luận.
Lời giải chi tiết:
a) Góc giữa hai đường thẳng \(d\) và \(d'\) là góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) cùng đi qua một điểm và tương ứng song song (hoặc trùng) với \(d\) và \(d'\).
b) Ta có \(\vec b = \left( { - 2; - 1; - 3} \right) = - \vec a\) nên \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d\).
c) Do \(\vec a\) và \(\vec a'\) lần lượt là các vectơ chỉ phương của \(d\) và \(d'\), nên ta có \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right|\).
Ta có \(\vec a\) và \(\vec b\) là hai vectơ đối nhau, nên ta có \(\left( {\vec a,\vec a'} \right)\) và \(\left( {\vec b,\vec a'} \right)\) là hai góc bù nhau. Suy ra \(\left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
Như vậy \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Từ câu c, ta có côsin của góc giữa hai đường thẳng trong không gian là giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
TH10
Trả lời câu hỏi Thực hành 10 trang 56 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = 11 + 3t\\y = - 11 + t\\z = - 21 - 2t\end{array} \right.\) và \(\left( P \right):6x + 2y - 4z + 7 = 0.\)
b) \(d:\frac{{x - 3}}{2} = \frac{{y + 4}}{4} = \frac{{z - 5}}{2}\) và \(\left( P \right):2x + 2y - 4z + 1 = 0.\)
c) \(d:\frac{{x + 3}}{4} = \frac{{y + 5}}{4} = \frac{{z + 11}}{2}\) và \(\left( P \right):2y - 4z + 7 = 0.\)
Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của \(d\) và vectơ pháp tuyến \(\vec n\) của \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
a) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {3;1; - 2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {6;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {3.6 + 1.2 + \left( { - 2} \right).\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{6^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 1\).
Suy ra \(\left( {d,\left( P \right)} \right) = {90^o}\).
b) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {2;4;2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {2;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {2.2 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{2^2} + {4^2} + {2^2}} .\sqrt {{2^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = \frac{1}{6}\).
Suy ra \(\left( {d,\left( P \right)} \right) \approx {9^o}36'\).
c) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {4;4;2} \right).\)
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {0;2; - 4} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {4.0 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{4^2} + {4^2} + {2^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 0.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {0^o}.\)
TH11
Trả lời câu hỏi Thực hành 11 trang 58 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right):3x + 7y - z + 4 = 0\) và \(\left( {P'} \right):x + y - 10z + 2025 = 0.\)
b) \(\left( P \right):x + y - 2z + 9 = 0\) và \(\left( {P'} \right):3x - 5y + z + 2024 = 0.\)
c) \(\left( P \right):x + z + 3 = 0\) và \(\left( {P'} \right):3y + 3z + 5 = 0.\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\), sau đó sử dụng công thức \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\).
Lời giải chi tiết:
a) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {3;7; - 1} \right)\) và \(\vec n' = \left( {1;1; - 10} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {3.1 + 7.1 + \left( { - 1} \right).\left( { - 10} \right)} \right|}}{{\sqrt {{3^2} + {7^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2} + {{\left( { - 10} \right)}^2}} }} = \frac{{20}}{{\sqrt {6018} }}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {75^o}3'.\)
b) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {1;1; - 2} \right)\) và \(\vec n' = \left( {3; - 5;1} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.3 + 1.\left( { - 5} \right) + \left( { - 2} \right).1} \right|}}{{\sqrt {{1^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{3^2} + {{\left( { - 5} \right)}^2} + {1^2}} }} = \frac{{2\sqrt {210} }}{{105}}\).
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {73^o}59'.\)
c) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {1;0;1} \right)\) và \(\vec n' = \left( {0;3;3} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.0 + 0.3 + 1.3} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {3^2}} }} = \frac{1}{2}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = {30^o}.\)
TH12
Trả lời câu hỏi Thực hành 12 trang 59 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Cho biết \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Tính góc giữa:
a) hai đường thẳng \(AC\) và \(BA'.\)
b) hai mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right).\)
c) đường thẳng \(AC'\) và mặt phẳng \(\left( {A'BD} \right).\)
Phương pháp giải:
a) Xác định các vectơ chỉ phương của các đường thẳng \(AC\) và \(BA'\), côsin góc giữa hai đường thẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
b) Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
c) Xác định vectơ chỉ phương của đường thẳng \(AC'\) và vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\), sin góc giữa đường thẳng và mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
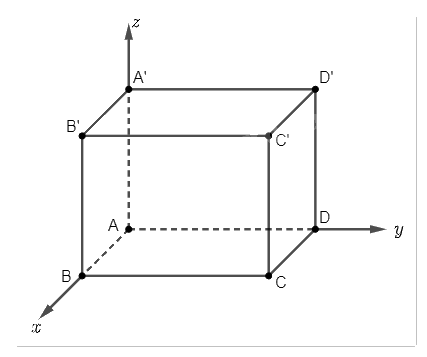
a) Ta có \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\), suy ra \(C\left( {1;5;0} \right).\)
Suy ra \(\overrightarrow {AC} = \left( {1;5;0} \right)\) và \(\overrightarrow {BA'} = \left( { - 1;0;3} \right).\)
Ta có \(\cos \left( {AC,BA'} \right) = \left| {\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA'} } \right)} \right| = \frac{{\left| {1.\left( { - 1} \right) + 5.0 + 0.3} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {0^2} + {3^2}} }} = \frac{{\sqrt {65} }}{{130}}\).
Vậy \(\left( {AC,BA'} \right) \approx {86^o}27'.\)
b) Ta có \(BB' \bot AC\) và \[DB \bot AC\] nên \(\overrightarrow {AC} = \left( {1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {BB'D'D} \right).\)
Ta có \(CC' \bot BD\) và \[AC \bot BD\] nên \(\overrightarrow {BD} = \left( { - 1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {AA'C'C} \right).\)
Như vậy,
\(\cos \left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) = \left| {\cos \left( {\overrightarrow {BD} ,\overrightarrow {AC} } \right)} \right| = \frac{{\left| {1.\left( { - 1} \right) + 5.5 + 0.0} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} \sqrt {{{\left( { - 1} \right)}^2} + {5^2} + {0^2}} }} = \frac{{12}}{{13}}.\)
Suy ra \(\left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) \approx {22^o}37'\).
c) Ta có \(C'\left( {1;5;3} \right) \Rightarrow \overrightarrow {AC'} = \left( {1;5;3} \right).\)
Ta có \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Suy ra mặt phẳng \(\left( {A'BD} \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {A'B} \left( {1;0; - 3} \right)\) và \(\overrightarrow {A'D} \left( {0;5; - 3} \right)\). Suy ra một vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right] = \left( {15;3;5} \right).\)
Ta có \(\sin \left( {AC',\left( {A'BD} \right)} \right) = \left| {\cos \left( {\overrightarrow {AC'} ,\vec n} \right)} \right| = \frac{{\left| {1.15 + 5.3 + 3.5} \right|}}{{\sqrt {{1^2} + {5^2} + {3^2}} .\sqrt {{{15}^2} + {3^2} + {5^2}} }} = \frac{{9\sqrt {185} }}{{259}}.\)
Suy ra \(\left( {AC',\left( {A'BD} \right)} \right) \approx {28^o}12'.\)
HĐ10
Trả lời câu hỏi Hoạt động 10 trang 57 SGK Toán 12 Chân trời sáng tạo
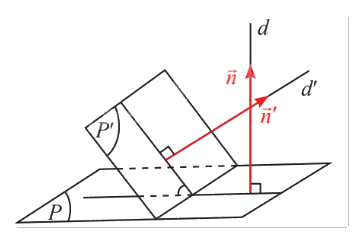
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) có vectơ pháp tuyến lần lượt là \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\), \(\vec n' = \left( {{n_1}';{n_2}';{n_3}'} \right)\) (hình dưới dây).
Gọi \(d\) và \(d'\) là hai đường thẳng lần lượt vuông góc với \(\left( P \right)\) và \(\left( {P'} \right)\). Gốc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\). So sánh \(\cos \left( {\left( P \right),\left( {P'} \right)} \right)\) và \(\cos \left( {\vec n,\vec n'} \right).\)
Phương pháp giải:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), từ đó rút ra kết luận.
Lời giải chi tiết:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), nên suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = \left( {d,d'} \right).\)
Như vậy \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \cos \left( {d,d'} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\). (Do \(\vec n\) và \(\vec n'\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(d'.\)
VD5
Trả lời câu hỏi Vận dụng 5 trang 55 SGK Toán 12 Chân trời sáng tạo
Trên một phần mềm đã thiết kế sân khấu 3D trong không gian \(Oxyz\). Tính góc giữa hai tia sáng có phương trình lần lượt là: \(d:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\) và \(d':\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\) (hình dưới đây).

Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
Tia sáng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 1} \right)\).
Tia sáng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {3;3;9} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.3 + 1.3 + \left( { - 1} \right).9} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {3^2} + {9^2}} }} = 0\).
Suy ra \(\left( {d,d'} \right) = {90^o}\).
VD7
Trả lời câu hỏi Vận dụng 7 trang 59 SGK Toán 12 Chân trời sáng tạo
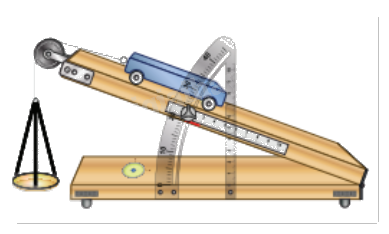
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa mặt phẳng nghiêng \(\left( P \right):4x + 11z + 5 = 0\) và mặt sàn \(\left( Q \right):z - 1 = 0.\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của mặt phẳng nghiêng \(\left( P \right)\) và mặt sàn \(\left( Q \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
Mặt phẳng nghiêng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( P \right)}}} = \left( {4;0;11} \right).\)
Mặt sàn \(\left( Q \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( Q \right)}}} = \left( {0;0;1} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_{\left( P \right)}}} ,\overrightarrow {{n_{\left( Q \right)}}} } \right)} \right| = \frac{{\left| {4.0 + 0.0 + 11.1} \right|}}{{\sqrt {{4^2} + {0^2} + {{11}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{11}}{{\sqrt {137} }}.\)
Suy ra \(\left( {\left( P \right),\left( Q \right)} \right) \approx {19^o}59'.\)
VD6
Trả lời câu hỏi Vận dụng 6 trang 56 SGK Toán 12 Chân trời sáng tạo
Đề bài:
Trên một sân khấu đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa tia sáng có phương trình \(d:\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 1 + t\end{array} \right.\) và măt sàn sân khấu có phương trình \(z = 0.\)

Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của tia sáng \(d\) và vectơ pháp tuyến \(\vec n\) của mặt sân khấu \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
Một vectơ chỉ phương của tia sáng \(d\) là \(\vec a = \left( {0;1;1} \right)\).
Một vectơ pháp tuyến của mặt sân khấu \(\left( P \right)\) là
\(\vec n = \left( {0;0;1} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {0.0 + 1.0 + 1.1} \right|}}{{\sqrt {{0^2} + {1^2} + {1^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {45^o}.\)
HĐ9
Trả lời câu hỏi Hoạt động 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) và mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\). Biết \(d\) cắt \(\left( P \right)\) tại điểm \(N\) và hình chiếu vuông góc của \(d\) lên \(\left( P \right)\) là đường thẳng \(d'\). Qua \(N\) vẽ đường thẳng \(\Delta \) vuông góc với \(\left( P \right)\) (hình dưới đây).
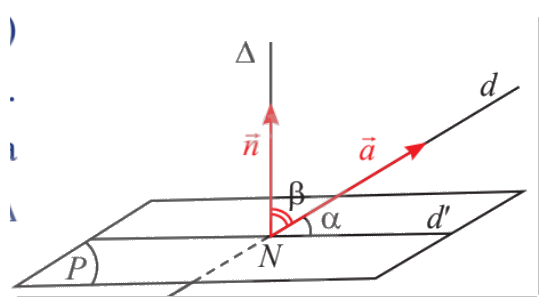
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
b) Có nhận xét gì về số đo hai góc \(\alpha = \left( {d,d'} \right)\); \(\beta = \left( {\Delta ,d} \right)\)?
c) Giải thích tại sao ta lại có đẳng thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\).
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng đã được học ở các lớp dưới.
b) Chỉ ra rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}\).
c) Từ câu b, rút ra kết luận.
Lời giải chi tiết:
a) Nếu đường thẳng \(a\) vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là \({90^o}\).
Nếu đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu \(a'\) của \(a\) trên \(\left( P \right).\)
b) Nhìn vào hình vẽ, ta thấy rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}.\)
c) Do \(\alpha + \beta = {90^o}\) nên ta có \(\sin \alpha = \cos \beta .\)
Ta có \(d'\) là hình chiếu vuông góc của \(d\) lên \(\left( P \right)\), nên \(\alpha = \left( {d,d'} \right) = \left( {d,\left( P \right)} \right).\)
Ta có \(\beta = \left( {\Delta ,d} \right)\) nên \(\cos \beta = \cos \left( {\Delta ,d} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\). (Vì \(\vec a\) và \(\vec n\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(\Delta \)).
Mà \(\sin \alpha = \cos \beta \) nên \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
- HĐ8
- TH9
- VD5
- HĐ9
- TH10
- VD6
- HĐ10
- TH11
- TH12
- VD7
Trả lời câu hỏi Hoạt động 8 trang 53 SGK Toán 12 Chân trời sáng tạo
Cho hai đường thẳng \(d\) và \(d'\) có vectơ chỉ phương lần lượt là \(\vec a = \left( {2;1;3} \right)\) và \(\vec a' = \left( {3;2; - 8} \right)\).
a) Nhắc lại định nghĩa góc giữa hai đường thẳng \(d\) và \(d'\) trong không gian.
b) Vectơ \(\vec b = \left( { - 2;; - 1; - 3} \right)\) có phải là một vectơ chỉ phương của \(d\) không?
c) Giải thích tại sao ta lại có đẳng thức \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa hai đường thẳng trong không gian đã được học ở các lớp dưới.
b) Kiểm tra xem \(\vec b\) có cùng phương với vectơ \(\vec a\) không.
c) Do góc của hai đường thẳng lớn nhất là 90 độ, còn góc giữa hai vectơ lớn nhất là 180 độ.
d) Từ câu c, rút ra kết luận.
Lời giải chi tiết:
a) Góc giữa hai đường thẳng \(d\) và \(d'\) là góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) cùng đi qua một điểm và tương ứng song song (hoặc trùng) với \(d\) và \(d'\).
b) Ta có \(\vec b = \left( { - 2; - 1; - 3} \right) = - \vec a\) nên \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d\).
c) Do \(\vec a\) và \(\vec a'\) lần lượt là các vectơ chỉ phương của \(d\) và \(d'\), nên ta có \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right|\).
Ta có \(\vec a\) và \(\vec b\) là hai vectơ đối nhau, nên ta có \(\left( {\vec a,\vec a'} \right)\) và \(\left( {\vec b,\vec a'} \right)\) là hai góc bù nhau. Suy ra \(\left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
Như vậy \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Từ câu c, ta có côsin của góc giữa hai đường thẳng trong không gian là giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Trả lời câu hỏi Thực hành 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai đường thẳng \(d\) và \(d'\) trong mỗi trường hợp sau:
a) \(d:\frac{{x - 7}}{3} = \frac{y}{5} = \frac{{z - 11}}{4}\) và \(d':\frac{{x - 3}}{2} = \frac{{y + 6}}{5} = \frac{{z - 1}}{{ - 4}}.\)
b) \(d:\frac{{x + 9}}{3} = \frac{{y + 4}}{6} = \frac{{z + 1}}{6}\) và \(d':\left\{ \begin{array}{l}x = 9 - 10t\\y = 7 - 10t\\z = 15 + 5t\end{array} \right.\).
c) \(d:\left\{ \begin{array}{l}x = 23 + 2t\\y = 57 + t\\z = 19 - 5t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 24 + t'\\y = 6 + t'\\z = t'\end{array} \right.\).
Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
a) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;5;4} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {2;5; - 4} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.2 + 5.5 + 4.\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {5^2} + {4^2}} .\sqrt {{2^2} + {5^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{\sqrt {10} }}{{10}}\).
Suy ra \(\left( {d,d'} \right) \approx {71^o}34'\).
b) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;6;6} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( { - 10; - 10;5} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.\left( { - 10} \right) + 6.\left( { - 10} \right) + 6.5} \right|}}{{\sqrt {{3^2} + {6^2} + {6^2}} .\sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2} + {5^2}} }} = \frac{4}{9}\).
Suy ra \(\left( {d,d'} \right) \approx {63^o}37'\).
c) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 5} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {1;1;1} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.1 + 1.1 + \left( { - 5} \right).1} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 5} \right)}^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{\sqrt {10} }}{{15}}\).
Suy ra \(\left( {d,d'} \right) \approx {77^o}50'\).
Trả lời câu hỏi Vận dụng 5 trang 55 SGK Toán 12 Chân trời sáng tạo
Trên một phần mềm đã thiết kế sân khấu 3D trong không gian \(Oxyz\). Tính góc giữa hai tia sáng có phương trình lần lượt là: \(d:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\) và \(d':\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\) (hình dưới đây).

Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
Tia sáng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 1} \right)\).
Tia sáng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {3;3;9} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.3 + 1.3 + \left( { - 1} \right).9} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {3^2} + {9^2}} }} = 0\).
Suy ra \(\left( {d,d'} \right) = {90^o}\).
Trả lời câu hỏi Hoạt động 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) và mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\). Biết \(d\) cắt \(\left( P \right)\) tại điểm \(N\) và hình chiếu vuông góc của \(d\) lên \(\left( P \right)\) là đường thẳng \(d'\). Qua \(N\) vẽ đường thẳng \(\Delta \) vuông góc với \(\left( P \right)\) (hình dưới đây).
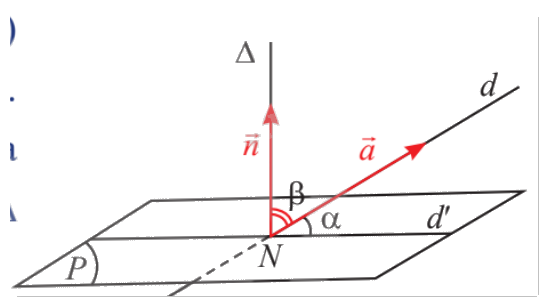
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
b) Có nhận xét gì về số đo hai góc \(\alpha = \left( {d,d'} \right)\); \(\beta = \left( {\Delta ,d} \right)\)?
c) Giải thích tại sao ta lại có đẳng thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\).
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng đã được học ở các lớp dưới.
b) Chỉ ra rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}\).
c) Từ câu b, rút ra kết luận.
Lời giải chi tiết:
a) Nếu đường thẳng \(a\) vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là \({90^o}\).
Nếu đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu \(a'\) của \(a\) trên \(\left( P \right).\)
b) Nhìn vào hình vẽ, ta thấy rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}.\)
c) Do \(\alpha + \beta = {90^o}\) nên ta có \(\sin \alpha = \cos \beta .\)
Ta có \(d'\) là hình chiếu vuông góc của \(d\) lên \(\left( P \right)\), nên \(\alpha = \left( {d,d'} \right) = \left( {d,\left( P \right)} \right).\)
Ta có \(\beta = \left( {\Delta ,d} \right)\) nên \(\cos \beta = \cos \left( {\Delta ,d} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\). (Vì \(\vec a\) và \(\vec n\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(\Delta \)).
Mà \(\sin \alpha = \cos \beta \) nên \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Trả lời câu hỏi Thực hành 10 trang 56 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = 11 + 3t\\y = - 11 + t\\z = - 21 - 2t\end{array} \right.\) và \(\left( P \right):6x + 2y - 4z + 7 = 0.\)
b) \(d:\frac{{x - 3}}{2} = \frac{{y + 4}}{4} = \frac{{z - 5}}{2}\) và \(\left( P \right):2x + 2y - 4z + 1 = 0.\)
c) \(d:\frac{{x + 3}}{4} = \frac{{y + 5}}{4} = \frac{{z + 11}}{2}\) và \(\left( P \right):2y - 4z + 7 = 0.\)
Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của \(d\) và vectơ pháp tuyến \(\vec n\) của \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
a) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {3;1; - 2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {6;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {3.6 + 1.2 + \left( { - 2} \right).\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{6^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 1\).
Suy ra \(\left( {d,\left( P \right)} \right) = {90^o}\).
b) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {2;4;2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {2;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {2.2 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{2^2} + {4^2} + {2^2}} .\sqrt {{2^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = \frac{1}{6}\).
Suy ra \(\left( {d,\left( P \right)} \right) \approx {9^o}36'\).
c) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {4;4;2} \right).\)
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {0;2; - 4} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {4.0 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{4^2} + {4^2} + {2^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 0.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {0^o}.\)
Trả lời câu hỏi Vận dụng 6 trang 56 SGK Toán 12 Chân trời sáng tạo
Đề bài:
Trên một sân khấu đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa tia sáng có phương trình \(d:\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 1 + t\end{array} \right.\) và măt sàn sân khấu có phương trình \(z = 0.\)

Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của tia sáng \(d\) và vectơ pháp tuyến \(\vec n\) của mặt sân khấu \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
Một vectơ chỉ phương của tia sáng \(d\) là \(\vec a = \left( {0;1;1} \right)\).
Một vectơ pháp tuyến của mặt sân khấu \(\left( P \right)\) là
\(\vec n = \left( {0;0;1} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {0.0 + 1.0 + 1.1} \right|}}{{\sqrt {{0^2} + {1^2} + {1^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {45^o}.\)
Trả lời câu hỏi Hoạt động 10 trang 57 SGK Toán 12 Chân trời sáng tạo
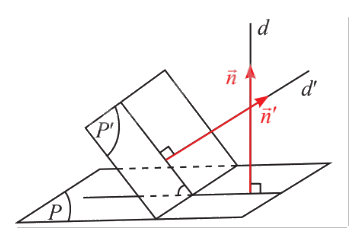
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) có vectơ pháp tuyến lần lượt là \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\), \(\vec n' = \left( {{n_1}';{n_2}';{n_3}'} \right)\) (hình dưới dây).
Gọi \(d\) và \(d'\) là hai đường thẳng lần lượt vuông góc với \(\left( P \right)\) và \(\left( {P'} \right)\). Gốc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\). So sánh \(\cos \left( {\left( P \right),\left( {P'} \right)} \right)\) và \(\cos \left( {\vec n,\vec n'} \right).\)
Phương pháp giải:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), từ đó rút ra kết luận.
Lời giải chi tiết:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), nên suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = \left( {d,d'} \right).\)
Như vậy \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \cos \left( {d,d'} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\). (Do \(\vec n\) và \(\vec n'\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(d'.\)
Trả lời câu hỏi Thực hành 11 trang 58 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right):3x + 7y - z + 4 = 0\) và \(\left( {P'} \right):x + y - 10z + 2025 = 0.\)
b) \(\left( P \right):x + y - 2z + 9 = 0\) và \(\left( {P'} \right):3x - 5y + z + 2024 = 0.\)
c) \(\left( P \right):x + z + 3 = 0\) và \(\left( {P'} \right):3y + 3z + 5 = 0.\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\), sau đó sử dụng công thức \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\).
Lời giải chi tiết:
a) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {3;7; - 1} \right)\) và \(\vec n' = \left( {1;1; - 10} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {3.1 + 7.1 + \left( { - 1} \right).\left( { - 10} \right)} \right|}}{{\sqrt {{3^2} + {7^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2} + {{\left( { - 10} \right)}^2}} }} = \frac{{20}}{{\sqrt {6018} }}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {75^o}3'.\)
b) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {1;1; - 2} \right)\) và \(\vec n' = \left( {3; - 5;1} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.3 + 1.\left( { - 5} \right) + \left( { - 2} \right).1} \right|}}{{\sqrt {{1^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{3^2} + {{\left( { - 5} \right)}^2} + {1^2}} }} = \frac{{2\sqrt {210} }}{{105}}\).
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {73^o}59'.\)
c) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {1;0;1} \right)\) và \(\vec n' = \left( {0;3;3} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.0 + 0.3 + 1.3} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {3^2}} }} = \frac{1}{2}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = {30^o}.\)
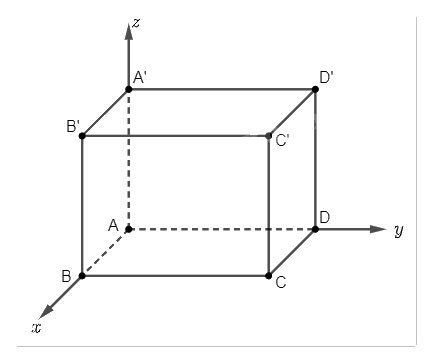
Trả lời câu hỏi Thực hành 12 trang 59 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Cho biết \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Tính góc giữa:
a) hai đường thẳng \(AC\) và \(BA'.\)
b) hai mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right).\)
c) đường thẳng \(AC'\) và mặt phẳng \(\left( {A'BD} \right).\)
Phương pháp giải:
a) Xác định các vectơ chỉ phương của các đường thẳng \(AC\) và \(BA'\), côsin góc giữa hai đường thẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
b) Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
c) Xác định vectơ chỉ phương của đường thẳng \(AC'\) và vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\), sin góc giữa đường thẳng và mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
a) Ta có \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\), suy ra \(C\left( {1;5;0} \right).\)
Suy ra \(\overrightarrow {AC} = \left( {1;5;0} \right)\) và \(\overrightarrow {BA'} = \left( { - 1;0;3} \right).\)
Ta có \(\cos \left( {AC,BA'} \right) = \left| {\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA'} } \right)} \right| = \frac{{\left| {1.\left( { - 1} \right) + 5.0 + 0.3} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {0^2} + {3^2}} }} = \frac{{\sqrt {65} }}{{130}}\).
Vậy \(\left( {AC,BA'} \right) \approx {86^o}27'.\)
b) Ta có \(BB' \bot AC\) và \[DB \bot AC\] nên \(\overrightarrow {AC} = \left( {1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {BB'D'D} \right).\)
Ta có \(CC' \bot BD\) và \[AC \bot BD\] nên \(\overrightarrow {BD} = \left( { - 1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {AA'C'C} \right).\)
Như vậy,
\(\cos \left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) = \left| {\cos \left( {\overrightarrow {BD} ,\overrightarrow {AC} } \right)} \right| = \frac{{\left| {1.\left( { - 1} \right) + 5.5 + 0.0} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} \sqrt {{{\left( { - 1} \right)}^2} + {5^2} + {0^2}} }} = \frac{{12}}{{13}}.\)
Suy ra \(\left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) \approx {22^o}37'\).
c) Ta có \(C'\left( {1;5;3} \right) \Rightarrow \overrightarrow {AC'} = \left( {1;5;3} \right).\)
Ta có \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Suy ra mặt phẳng \(\left( {A'BD} \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {A'B} \left( {1;0; - 3} \right)\) và \(\overrightarrow {A'D} \left( {0;5; - 3} \right)\). Suy ra một vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right] = \left( {15;3;5} \right).\)
Ta có \(\sin \left( {AC',\left( {A'BD} \right)} \right) = \left| {\cos \left( {\overrightarrow {AC'} ,\vec n} \right)} \right| = \frac{{\left| {1.15 + 5.3 + 3.5} \right|}}{{\sqrt {{1^2} + {5^2} + {3^2}} .\sqrt {{{15}^2} + {3^2} + {5^2}} }} = \frac{{9\sqrt {185} }}{{259}}.\)
Suy ra \(\left( {AC',\left( {A'BD} \right)} \right) \approx {28^o}12'.\)
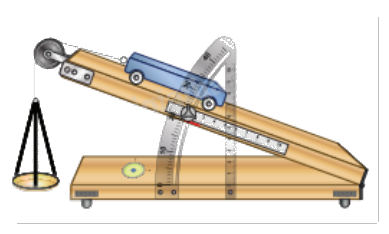
Trả lời câu hỏi Vận dụng 7 trang 59 SGK Toán 12 Chân trời sáng tạo
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa mặt phẳng nghiêng \(\left( P \right):4x + 11z + 5 = 0\) và mặt sàn \(\left( Q \right):z - 1 = 0.\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của mặt phẳng nghiêng \(\left( P \right)\) và mặt sàn \(\left( Q \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
Mặt phẳng nghiêng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( P \right)}}} = \left( {4;0;11} \right).\)
Mặt sàn \(\left( Q \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( Q \right)}}} = \left( {0;0;1} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_{\left( P \right)}}} ,\overrightarrow {{n_{\left( Q \right)}}} } \right)} \right| = \frac{{\left| {4.0 + 0.0 + 11.1} \right|}}{{\sqrt {{4^2} + {0^2} + {{11}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{11}}{{\sqrt {137} }}.\)
Suy ra \(\left( {\left( P \right),\left( Q \right)} \right) \approx {19^o}59'.\)
Giải mục 3 trang 53, 54, 55, 65, 57, 58, 59 SGK Toán 12 tập 2 - Chân trời sáng tạo: Tổng quan
Mục 3 trong SGK Toán 12 tập 2 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết các bài tập trong mục này một cách hiệu quả, học sinh cần nắm vững kiến thức lý thuyết, các định nghĩa, định lý và công thức liên quan. Tusach.vn sẽ cung cấp lời giải chi tiết cho từng trang, giúp các em hiểu rõ phương pháp giải và áp dụng vào các bài tập tương tự.
Giải chi tiết từng trang
Trang 53 - 55: Bài tập về... (Ví dụ: Đạo hàm của hàm số lượng giác)
Ở trang này, các em sẽ được làm quen với các bài tập về đạo hàm của các hàm số lượng giác. Để giải các bài tập này, các em cần nhớ các công thức đạo hàm cơ bản của sinx, cosx, tanx, cotx. Ví dụ:
- (sinx)' = cosx
- (cosx)' = -sinx
Chúng ta sẽ cùng giải một ví dụ:
Bài tập: Tính đạo hàm của hàm số y = 2sin(x) + 3cos(x)
Lời giải:
y' = 2(sinx)' + 3(cosx)' = 2cosx - 3sinx
Trang 57 - 59: Bài tập về... (Ví dụ: Ứng dụng đạo hàm để khảo sát hàm số)
Trang 57-59 tập trung vào việc ứng dụng đạo hàm để khảo sát hàm số, bao gồm tìm cực trị, khoảng đồng biến, nghịch biến. Để làm được điều này, các em cần:
- Tính đạo hàm cấp nhất y'
- Tìm các điểm mà y' = 0 hoặc không xác định
- Lập bảng biến thiên để xác định khoảng đồng biến, nghịch biến và cực trị
Trang 65: Bài tập tổng hợp
Trang 65 thường chứa các bài tập tổng hợp, đòi hỏi học sinh phải vận dụng kiến thức từ nhiều phần khác nhau trong chương. Đây là cơ hội để các em rèn luyện kỹ năng giải quyết vấn đề và củng cố kiến thức đã học.
Mẹo học tập hiệu quả
- Nắm vững lý thuyết: Trước khi bắt tay vào giải bài tập, hãy đảm bảo rằng các em đã hiểu rõ các định nghĩa, định lý và công thức liên quan.
- Luyện tập thường xuyên: Giải càng nhiều bài tập, các em càng trở nên thành thạo và tự tin hơn.
- Sử dụng tài liệu tham khảo: Ngoài SGK, các em có thể tham khảo thêm các tài liệu tham khảo khác để mở rộng kiến thức và tìm hiểu các phương pháp giải khác nhau.
- Hỏi thầy cô giáo: Nếu gặp khó khăn, đừng ngần ngại hỏi thầy cô giáo để được hướng dẫn và giải đáp.
Kết luận
Hy vọng rằng với lời giải chi tiết và những lời khuyên hữu ích trên, các em sẽ học tốt môn Toán 12 tập 2 Chân trời sáng tạo. Tusach.vn luôn sẵn sàng đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em thành công!