Giải bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo là một phần quan trọng trong chương trình học Toán 12. Bài tập này thường tập trung vào việc vận dụng các kiến thức về giới hạn của hàm số để giải quyết các bài toán thực tế.
tusach.vn cung cấp lời giải chi tiết, dễ hiểu, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5N. Tính cường độ của hợp lực.
Đề bài
Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với ba cạnh và cùng có cường độ là 5N. Tính cường độ của hợp lực.
Phương pháp giải - Xem chi tiết
Áp dụng quy tắc hình hộp
Lời giải chi tiết
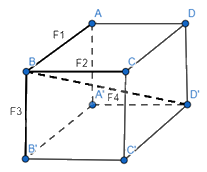
Vecto hợp lực là: \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} + \overrightarrow {{F_3}} = \overrightarrow {{F_4}} \)
Cường độ của hợp lực là: \({F_4} = \sqrt {{F_{12}}^2 + F_3^2} = \sqrt {{{({F_1}^2 + F_2^2)}^2} + F_3^2} = \sqrt {{5^2} + {5^2} + {5^2}} = 5\sqrt 3 N\)
Giải bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo: Hướng dẫn chi tiết và dễ hiểu
Bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo thuộc chương trình học về giới hạn của hàm số. Đây là một chủ đề quan trọng, nền tảng cho các kiến thức toán học nâng cao hơn. Bài viết này sẽ cung cấp hướng dẫn chi tiết, dễ hiểu để giúp các em học sinh giải quyết bài tập này một cách hiệu quả.
Nội dung bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
Bài tập 3 thường yêu cầu học sinh tính giới hạn của hàm số tại một điểm, hoặc khi x tiến tới vô cùng. Để giải quyết bài tập này, các em cần nắm vững các định nghĩa và tính chất của giới hạn, cũng như các phương pháp tính giới hạn thường gặp.
Các phương pháp giải bài tập giới hạn thường gặp
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn. Phương pháp này chỉ áp dụng được khi hàm số liên tục tại điểm đó.
- Phương pháp phân tích thành nhân tử: Phân tích tử số và mẫu số thành nhân tử để rút gọn biểu thức, sau đó thay giá trị của x vào để tính giới hạn.
- Phương pháp nhân liên hợp: Nhân cả tử số và mẫu số với liên hợp của biểu thức để khử dạng vô định.
- Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn đã học để tính giới hạn.
Lời giải chi tiết bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo
Để minh họa, chúng ta sẽ cùng giải một ví dụ cụ thể. Giả sử bài tập 3 có nội dung như sau:
Bài tập: Tính limx→2 (x2 - 4) / (x - 2)
Lời giải:
- Ta phân tích tử số thành nhân tử: x2 - 4 = (x - 2)(x + 2)
- Thay vào biểu thức ban đầu, ta có: limx→2 (x - 2)(x + 2) / (x - 2)
- Rút gọn biểu thức: limx→2 (x + 2)
- Thay x = 2 vào biểu thức, ta được: 2 + 2 = 4
- Vậy, limx→2 (x2 - 4) / (x - 2) = 4
Lưu ý khi giải bài tập giới hạn
- Luôn kiểm tra xem hàm số có liên tục tại điểm cần tính giới hạn hay không.
- Sử dụng các phương pháp giải phù hợp với từng dạng bài tập.
- Kiểm tra lại kết quả sau khi tính toán.
Tài liệu tham khảo và hỗ trợ thêm
Ngoài SGK Toán 12 tập 1 - Chân trời sáng tạo, các em có thể tham khảo thêm các tài liệu sau:
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến uy tín như tusach.vn
- Hỏi thầy cô giáo hoặc bạn bè để được hỗ trợ.
Hy vọng bài viết này đã cung cấp cho các em những kiến thức và kỹ năng cần thiết để giải quyết bài tập 3 trang 50 SGK Toán 12 tập 1 - Chân trời sáng tạo một cách hiệu quả. Chúc các em học tập tốt!