Tusach.vn xin giới thiệu lời giải chi tiết bài tập mục 2 trang 21 SGK Toán 12 tập 1 Chân trời sáng tạo. Bài viết này cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp học sinh hiểu sâu kiến thức và tự tin làm bài tập.

Chúng tôi luôn cập nhật nhanh chóng và chính xác lời giải các bài tập trong SGK Toán 12 tập 1 Chân trời sáng tạo.

Đường tiệm cận ngang

TH2 KP2

TH2

Trả lời câu hỏi Thực hành 2 trang 21 SGK Toán 12 Chân trời sáng tạo

Tìm tiệm cận ngang của đồ thị các hàm số sau:

a) \(f(x) = \frac{{x - 1}}{{4x + 1}}\)

b) \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)

Phương pháp giải:

Đường thẳng y = m được gọi là một đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số y = f(x) nếu \(\mathop {\lim }\limits_{x \to - \infty } f(x) = m\) hoặc \(\mathop {\lim }\limits_{x \to + \infty } f(x) = m\)

Lời giải chi tiết:

a) Xét \(f(x) = \frac{{x - 1}}{{4x + 1}}\)

Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{4}} \right\}\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } f(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to + \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\); \(\mathop {\lim }\limits_{x \to - \infty } f(x) = \mathop {\lim }\limits_{x \to - \infty } \frac{{x - 1}}{{4x + 1}} = \mathop {\lim }\limits_{x \to - \infty } \frac{{1 - \frac{1}{x}}}{{4 + \frac{1}{x}}} = \frac{1}{4}\)

Vậy đường thẳng \(y = \frac{1}{4}\) là tiệm cận ngang của đồ thị hàm số

b) Xét \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)

Tập xác định: \(D = [0; + \infty )\)

Ta có: \(\mathop {\lim }\limits_{x \to + \infty } g(x) = \mathop {\lim }\limits_{x \to + \infty } \frac{{\sqrt x }}{{\sqrt x + 2}} = \mathop {\lim }\limits_{x \to + \infty } \frac{1}{{1 + \frac{2}{{\sqrt x }}}} = 1\)

Vậy đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số

Lựa chọn câu để xem lời giải nhanh hơn

Trả lời câu hỏi Khám phá 2 trang 21 SGK Toán 12 Chân trời sáng tạo

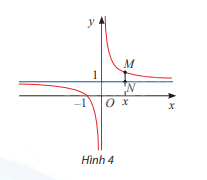
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.

a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x}\)

b) Đường thẳng vuông góc với trục Ox tại điểm x cắt đồ thị hàm số tại điểm M và cắt đường thẳng y = 1 tại điểm N (Hình 4). Tính MN theo x và nhận xét về MN khi \(x \to + \infty \) hoặc \(x \to - \infty \)

Giải mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo 1

Phương pháp giải:

Quan sát đồ thị

Lời giải chi tiết:

a) Từ đồ thị ta thấy:

Khi \(x \to + \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x} = 1\)

Khi \(x \to - \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x} = 1\)

b) MN = y – 1 = \(\frac{{x + 1}}{x} - 1 = \frac{1}{x}\)

Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0

Trả lời câu hỏi Thực hành 2 trang 21 SGK Toán 12 Chân trời sáng tạo

Tìm tiệm cận ngang của đồ thị các hàm số sau:

a) \(f(x) = \frac{{x - 1}}{{4x + 1}}\)

b) \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)

Phương pháp giải:

Lời giải chi tiết:

a) Xét \(f(x) = \frac{{x - 1}}{{4x + 1}}\)

Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - \frac{1}{4}} \right\}\)

Vậy đường thẳng \(y = \frac{1}{4}\) là tiệm cận ngang của đồ thị hàm số

b) Xét \(g(x) = \frac{{\sqrt x }}{{\sqrt x + 2}}\)

Tập xác định: \(D = [0; + \infty )\)

Vậy đường thẳng \(y = 1\) là tiệm cận ngang của đồ thị hàm số

KP2

Trả lời câu hỏi Khám phá 2 trang 21 SGK Toán 12 Chân trời sáng tạo

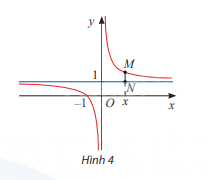
Cho hàm số \(y = \frac{{x + 1}}{x}\) có đồ thị như Hình 4.

a) Tìm \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x},\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x}\)

Giải mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo 0 1

Phương pháp giải:

Quan sát đồ thị

Lời giải chi tiết:

a) Từ đồ thị ta thấy:

Khi \(x \to + \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to + \infty } = \frac{{x + 1}}{x} = 1\)

Khi \(x \to - \infty \)thì y tiến dần đến \(1\), vậy \(\mathop {\lim }\limits_{x \to - \infty } = \frac{{x + 1}}{x} = 1\)

b) MN = y – 1 = \(\frac{{x + 1}}{x} - 1 = \frac{1}{x}\)

Khi \(x \to + \infty \) hoặc \(x \to - \infty \) thì MN tiến dần về 0

Giải mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo: Tổng quan và Phương pháp giải

Mục 2 trang 21 SGK Toán 12 tập 1 Chân trời sáng tạo thường tập trung vào các kiến thức về giới hạn hàm số. Đây là một phần quan trọng trong chương trình Toán 12, là nền tảng cho việc học các kiến thức về đạo hàm và tích phân. Việc nắm vững kiến thức và kỹ năng giải bài tập trong mục này là rất cần thiết để đạt kết quả tốt trong các kỳ thi.

Nội dung chính của Mục 2 trang 21

Khái niệm giới hạn hàm số tại một điểm: Hiểu rõ định nghĩa, điều kiện tồn tại giới hạn và các tính chất cơ bản.
Giới hạn một bên: Phân biệt giới hạn trái và giới hạn phải, điều kiện để giới hạn tồn tại.
Các dạng giới hạn thường gặp: Giới hạn vô cùng, giới hạn tại vô cùng, giới hạn của hàm đa thức, hàm hữu tỉ.
Ứng dụng của giới hạn: Tính giới hạn của hàm số, xét tính liên tục của hàm số.

Hướng dẫn giải bài tập Mục 2 trang 21 SGK Toán 12 tập 1 - Chân trời sáng tạo

Để giải tốt các bài tập trong mục này, học sinh cần:

Nắm vững định nghĩa và tính chất của giới hạn: Đây là cơ sở để giải quyết mọi bài toán liên quan đến giới hạn.
Sử dụng các phương pháp tính giới hạn:
- Phương pháp trực tiếp: Thay trực tiếp giá trị của x vào hàm số để tính giới hạn.
- Phương pháp phân tích thành nhân tử: Rút gọn biểu thức bằng cách phân tích thành nhân tử.
- Phương pháp nhân liên hợp: Nhân tử và mẫu với biểu thức liên hợp để khử dạng vô định.
- Phương pháp sử dụng định lý giới hạn: Áp dụng các định lý giới hạn để tính giới hạn.
Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập.

Ví dụ minh họa giải bài tập

Bài tập: Tính lim_x→2 (x² - 4) / (x - 2)

Giải:

Ta có: lim_x→2 (x² - 4) / (x - 2) = lim_x→2 (x - 2)(x + 2) / (x - 2) = lim_x→2 (x + 2) = 2 + 2 = 4

Lưu ý khi giải bài tập về giới hạn

Kiểm tra xem hàm số có xác định tại điểm cần tính giới hạn hay không.
Sử dụng đúng phương pháp tính giới hạn phù hợp với từng dạng bài tập.
Kiểm tra lại kết quả sau khi tính toán.

Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là địa chỉ tin cậy cung cấp lời giải chi tiết, chính xác và dễ hiểu cho các bài tập SGK Toán 12 tập 1 Chân trời sáng tạo. Chúng tôi cam kết mang đến cho học sinh những trải nghiệm học tập tốt nhất, giúp các em tự tin chinh phục môn Toán.

Ngoài ra, Tusach.vn còn cung cấp nhiều tài liệu học tập hữu ích khác như:

Bài giảng video: Giúp học sinh hiểu rõ hơn về các khái niệm và phương pháp giải bài tập.
Đề thi thử: Giúp học sinh làm quen với cấu trúc đề thi và rèn luyện kỹ năng làm bài.
Diễn đàn trao đổi: Nơi học sinh có thể trao đổi kiến thức, kinh nghiệm và giải đáp thắc mắc.

Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích và nâng cao kết quả học tập của bạn!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN

Giới Thiệu
Chính Sách Bảo Mật
Liên Hệ
Blog
Email: Taisachebook@gmail.com