Giải bài 9 trang 22 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 9 trang 22 SBT Toán 12 Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 9 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ các bài giải SBT Toán 12 Chân trời sáng tạo, hỗ trợ tối đa cho quá trình học tập của bạn.
Mặt cắt ngang của lòng máng dẫn nước là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 15 (phần được tô màu xám). Tính diện tích của mặt cắt ngang đó.
Đề bài
Mặt cắt ngang của lòng máng dẫn nước là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 15 (phần được tô màu xám). Tính diện tích của mặt cắt ngang đó.
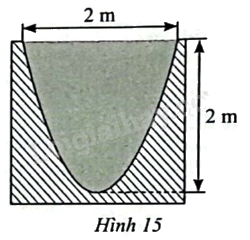
Phương pháp giải - Xem chi tiết
Gắn parabol vào hệ trục toạ độ \(Oxy\), sau đó sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right)} \right|dx} \).
Lời giải chi tiết
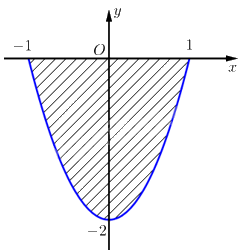
Chọn hệ trục toạ độ \(Oxy\) như hình vẽ.
Giả sử parabol có dạng \(y = a{x^2} - 2\left( {a > 0} \right)\).
Theo giả thiết ta có: \(y\left( 1 \right) = 0 \Leftrightarrow a{.1^2} - 2 = 0 \Leftrightarrow a = 2\).
Vậy phương trình đường parabol là \(y = 2{x^2} - 2\).
Diện tích của mặt cắt ngang là:
\(S = \int\limits_{ - 1}^1 {\left| {2{{\rm{x}}^2} - 2} \right|dx} = \int\limits_{ - 1}^1 {\left( { - 2{{\rm{x}}^2} + 2} \right)dx} = \left. {\left( { - \frac{{2{{\rm{x}}^3}}}{3} + 2x} \right)} \right|_{ - 1}^1 = \frac{8}{3}\left( {{m^2}} \right)\)
Giải bài 9 trang 22 SBT Toán 12 Chân trời sáng tạo: Chi tiết và Dễ Hiểu
Bài 9 trang 22 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Giới hạn. Đây là một bài tập quan trọng giúp học sinh củng cố kiến thức về giới hạn hàm số, giới hạn dãy số và ứng dụng của giới hạn trong việc tính đạo hàm.
Nội dung bài tập 9 trang 22 SBT Toán 12 Chân trời sáng tạo
Bài tập 9 thường bao gồm các dạng bài sau:
- Tính giới hạn hàm số: Yêu cầu tính giới hạn của hàm số tại một điểm hoặc khi x tiến tới vô cùng.
- Tính giới hạn dãy số: Yêu cầu tính giới hạn của dãy số khi n tiến tới vô cùng.
- Ứng dụng giới hạn để tính đạo hàm: Sử dụng định nghĩa đạo hàm thông qua giới hạn để tính đạo hàm của hàm số.
Lời giải chi tiết bài 9 trang 22 SBT Toán 12 Chân trời sáng tạo
Để giải bài 9 trang 22 SBT Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Định nghĩa giới hạn hàm số: Hiểu rõ định nghĩa giới hạn của hàm số tại một điểm và khi x tiến tới vô cùng.
- Định nghĩa giới hạn dãy số: Hiểu rõ định nghĩa giới hạn của dãy số khi n tiến tới vô cùng.
- Các quy tắc tính giới hạn: Nắm vững các quy tắc tính giới hạn của tổng, hiệu, tích, thương và lũy thừa của các hàm số và dãy số.
- Các giới hạn đặc biệt: Nhớ các giới hạn đặc biệt như lim (sin x)/x = 1 khi x -> 0, lim (1 + x)^n = e^n khi x -> 0.
Dưới đây là ví dụ về lời giải chi tiết một dạng bài tập thường gặp trong bài 9:
Ví dụ: Tính giới hạn \lim_{x \to 2} \frac{x^2 - 4}{x - 2}
Lời giải:
Ta có:
\lim_{x \to 2} \frac{x^2 - 4}{x - 2} = \lim_{x \to 2} \frac{(x - 2)(x + 2)}{x - 2} = \lim_{x \to 2} (x + 2) = 2 + 2 = 4
Mẹo giải bài tập về giới hạn
- Phân tích và đơn giản hóa biểu thức: Cố gắng phân tích và đơn giản hóa biểu thức trước khi tính giới hạn.
- Sử dụng các quy tắc tính giới hạn: Áp dụng các quy tắc tính giới hạn một cách linh hoạt.
- Sử dụng định nghĩa giới hạn: Trong một số trường hợp, cần sử dụng định nghĩa giới hạn để chứng minh sự tồn tại của giới hạn.
- Kiểm tra lại kết quả: Sau khi tính giới hạn, hãy kiểm tra lại kết quả để đảm bảo tính chính xác.
Tusach.vn – Hỗ trợ học tập Toán 12 hiệu quả
Tusach.vn không chỉ cung cấp lời giải chi tiết bài 9 trang 22 SBT Toán 12 Chân trời sáng tạo mà còn cung cấp đầy đủ các bài giải khác trong sách bài tập Toán 12 Chân trời sáng tạo. Chúng tôi cam kết mang đến cho bạn những tài liệu học tập chất lượng, giúp bạn học tập hiệu quả và đạt kết quả cao trong môn Toán.
Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu học tập hữu ích khác!
| Chương | Bài | Nội dung |
|---|---|---|
| 1 | 9 | Giới hạn hàm số |
| 2 | ... | Đạo hàm |