Giải bài 10 trang 22 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 10 trang 22 SBT Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.
Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để tự tin giải quyết các bài toán tương tự.
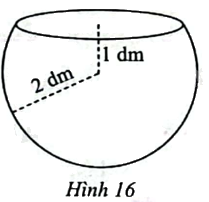
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối). Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số (y = sqrt {4 - {x^2}} ) với ( - 2 le x le 1), trục hoành và đường thẳng (x = 1) quanh trục hoành.
Đề bài
Một bể cá có dạng là một phần hình cầu được tạo thành khi cắt hình cầu bán kính 2 dm bằng mặt phẳng cách tâm của hình cầu 1 dm (Hình 16). Tính dung tích của bể cá (kết quả làm tròn đến hàng phần mười của đềximét khối).
Gợi ý: Có thể coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Phương pháp giải - Xem chi tiết
Gắn parabol vào hệ trục toạ độ \(Oxy\), sau đó sử dụng công thức: Tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = a,x = b\) quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {{{\left[ {f\left( x \right)} \right]}^2}dx} \).
Lời giải chi tiết
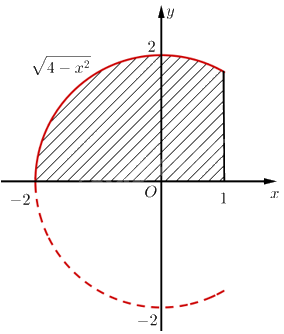
Chọn hệ trục toạ độ \(Oxy\) như hình vẽ.
Coi bể cá là khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi đồ thị hàm số \(y = \sqrt {4 - {x^2}} \) với \( - 2 \le x \le 1\), trục hoành và đường thẳng \(x = 1\) quanh trục hoành.
Dung tích của bể cá là:
\(V = \pi \int\limits_{ - 2}^1 {{{\left( {\sqrt {4 - {x^2}} } \right)}^2}dx} = \pi \int\limits_{ - 2}^1 {\left( {4 - {x^2}} \right)dx} = \left. {\pi \left( {4x - \frac{{{x^3}}}{3}} \right)} \right|_{ - 2}^1 = 9\pi \approx 28,3\left( {d{m^3}} \right)\).
Giải bài 10 trang 22 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo thường thuộc chương trình học về đạo hàm, tích phân hoặc các chủ đề khác tùy theo cấu trúc sách. Để giải quyết bài toán này một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản và áp dụng đúng phương pháp.
1. Xác định kiến thức cần thiết
Trước khi bắt đầu giải bài, hãy xác định rõ kiến thức toán học nào được yêu cầu. Ví dụ, nếu bài toán liên quan đến đạo hàm, bạn cần hiểu rõ các quy tắc tính đạo hàm, đạo hàm của các hàm số cơ bản và ứng dụng của đạo hàm trong việc tìm cực trị, khoảng đơn điệu của hàm số.
2. Phân tích đề bài và lập kế hoạch giải
Đọc kỹ đề bài, xác định rõ yêu cầu của bài toán. Sau đó, lập kế hoạch giải bằng cách chia bài toán thành các bước nhỏ hơn. Điều này giúp bạn tiếp cận bài toán một cách có hệ thống và tránh bỏ sót thông tin quan trọng.
3. Áp dụng kiến thức và giải bài toán
Sử dụng các kiến thức đã học và kế hoạch giải đã lập, tiến hành giải bài toán. Hãy trình bày các bước giải một cách rõ ràng, logic và dễ hiểu. Đừng quên kiểm tra lại kết quả để đảm bảo tính chính xác.
Giải chi tiết bài 10 trang 22 SBT Toán 12 Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. (Lưu ý: Nội dung giải bài cụ thể sẽ được chèn vào đây, tùy thuộc vào nội dung bài toán. Ví dụ:)
Bài 10: Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Giải:
- Tính đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm các điểm làm đạo hàm bậc nhất bằng 0: 3x2 - 6x = 0 => x = 0 hoặc x = 2
- Tính đạo hàm bậc hai: y'' = 6x - 6
- Kiểm tra dấu của đạo hàm bậc hai tại các điểm tìm được:
- Tại x = 0: y'' = -6 < 0 => Hàm số đạt cực đại tại x = 0, y = 2
- Tại x = 2: y'' = 6 > 0 => Hàm số đạt cực tiểu tại x = 2, y = -2
Vậy hàm số đạt cực đại tại điểm (0; 2) và cực tiểu tại điểm (2; -2).
Mẹo giải nhanh và các lưu ý
- Nắm vững các công thức đạo hàm và tích phân.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng máy tính bỏ túi để kiểm tra kết quả.
- Đọc kỹ đề bài và xác định rõ yêu cầu của bài toán.
Tài liệu tham khảo thêm
Để hiểu sâu hơn về các kiến thức liên quan, bạn có thể tham khảo thêm:
- Sách giáo khoa Toán 12
- Sách bài tập Toán 12
- Các trang web học Toán trực tuyến uy tín
Kết luận
Hy vọng bài giải chi tiết này đã giúp bạn hiểu rõ cách giải bài 10 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Hãy luyện tập thêm để nâng cao kỹ năng giải toán của mình. Chúc bạn học tốt!