Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạo
SBT Toán 12 - Chân trời sáng tạo
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
Chương 3. Các số đặc trưng đo mức độ phân tán cho mẫu số liệu ghép nhó
Bài 2. Phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm

Giải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 3 trang 104 SBT Toán 12 Chân trời sáng tạo

Bài 3 trang 104 sách bài tập Toán 12 Chân trời sáng tạo là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Tusach.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, giúp các em học sinh có thể tự tin làm bài tập và đạt kết quả tốt nhất.

Chiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau: Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

Đề bài

Chiều cao của một số cây giống sau khi nảy mầm được 4 tuần được biểu diễn ở bảng sau:

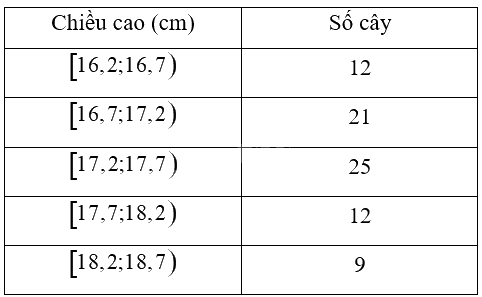
Giải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạo 1

Tính phương sai và độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).

Phương pháp giải - Xem chi tiếtGiải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạo 2

‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:

\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)

‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).

Lời giải chi tiết

Ta có bảng sau:

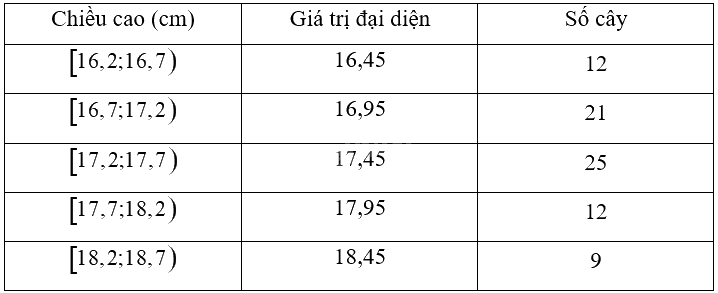
Giải bài 3 trang 104 sách bài tập toán 12 - Chân trời sáng tạo 3

Cỡ mẫu \(n = 12 + 21 + 25 + 12 + 9 = 79\)

Số trung bình của mẫu số liệu ghép nhóm là:

\(\overline x = \frac{{12.16,45 + 21.16,95 + 25.17,45 + 12.17,95 + 9.18,45}}{{79}} \approx 17,3551\)

Phương sai của mẫu số liệu ghép nhóm đó là:

\({S^2} = \frac{1}{{79}}\left( {{{12.16,45}^2} + {{21.16,95}^2} + {{25.17,45}^2} + {{12.17,95}^2} + {{9.18,45}^2}} \right) - {17,3551^2} \approx 0,36\)

Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S \approx \sqrt {0,36} \approx 0,6\).

Giải bài 3 trang 104 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 3 trang 104 sách bài tập Toán 12 Chân trời sáng tạo thường xoay quanh việc khảo sát hàm số bậc ba hoặc bậc bốn bằng phương pháp đạo hàm. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:

  1. Xác định tập xác định của hàm số: Kiểm tra xem có điều kiện nào về x hay không.
  2. Tính đạo hàm bậc nhất (y'): Sử dụng các quy tắc đạo hàm cơ bản để tìm y'.
  3. Tìm điểm tới hạn: Giải phương trình y' = 0 để tìm các điểm mà đạo hàm bằng không.
  4. Lập bảng biến thiên: Xác định dấu của y' trên các khoảng xác định bởi các điểm tới hạn. Từ đó, xác định khoảng đồng biến, nghịch biến và các điểm cực trị (cực đại, cực tiểu).
  5. Tính đạo hàm bậc hai (y''): Sử dụng các quy tắc đạo hàm để tìm y''.
  6. Tìm điểm uốn: Giải phương trình y'' = 0 để tìm các điểm uốn.
  7. Lập bảng biến thiên đầy đủ: Kết hợp thông tin từ đạo hàm bậc nhất và bậc hai để vẽ bảng biến thiên hoàn chỉnh.
  8. Kết luận về tính đơn điệu, cực trị và điểm uốn: Dựa vào bảng biến thiên để đưa ra kết luận cuối cùng.

Ví dụ minh họa: Giải bài 3 trang 104 SBT Toán 12 Chân trời sáng tạo (giả định)

Đề bài (giả định): Khảo sát hàm số y = x3 - 3x2 + 2.

Giải:

  1. Tập xác định: D = ℝ
  2. Đạo hàm bậc nhất: y' = 3x2 - 6x
  3. Điểm tới hạn: 3x2 - 6x = 0 => x = 0 hoặc x = 2
  4. Bảng biến thiên:

    x-∞02+∞
    y'+-+
    y↗↘↗
  5. Đạo hàm bậc hai: y'' = 6x - 6
  6. Điểm uốn: 6x - 6 = 0 => x = 1
  7. Kết luận: Hàm số đồng biến trên (-∞; 0) và (2; +∞), nghịch biến trên (0; 2). Hàm số đạt cực đại tại x = 0 với giá trị y = 2 và đạt cực tiểu tại x = 2 với giá trị y = -2. Hàm số có điểm uốn tại x = 1.

Lưu ý khi giải bài tập khảo sát hàm số

  • Luôn kiểm tra kỹ các bước tính đạo hàm.
  • Vẽ bảng biến thiên một cách cẩn thận để tránh sai sót.
  • Hiểu rõ ý nghĩa của đạo hàm bậc nhất và bậc hai trong việc xác định tính đơn điệu, cực trị và điểm uốn.
  • Thực hành nhiều bài tập khác nhau để nắm vững phương pháp.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn tự hào là một trong những nguồn tài liệu học tập Toán 12 uy tín và được nhiều học sinh tin dùng. Chúng tôi cung cấp đầy đủ lời giải chi tiết, bài tập trắc nghiệm và các tài liệu hỗ trợ học tập khác. Hãy truy cập Tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu hữu ích khác!

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN