Giải bài 4 trang 104 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 4 trang 104 SBT Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo. Tusach.vn cung cấp đáp án chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Bài viết này sẽ trình bày đầy đủ các bước giải, phân tích và giải thích chi tiết để bạn hiểu rõ bản chất của bài toán.
Bác Xuân biểu diễn thời gian tập thể dục mỗi ngày của mình trong 120 ngày liên tiếp ở biểu đồ tần số tương đối ghép nhóm dưới đây. a) Lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên. b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Đề bài
Bác Xuân biểu diễn thời gian tập thể dục mỗi ngày của mình trong 120 ngày liên tiếp ở biểu đồ tần số tương đối nghép nhóm dưới đây.
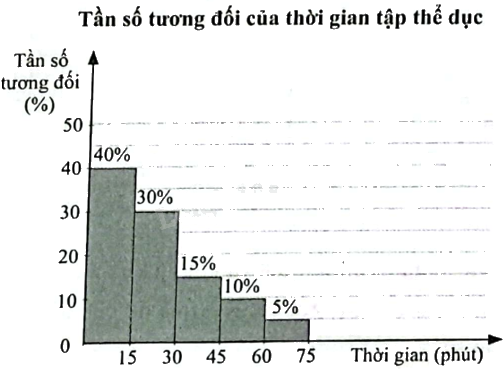
a) Lập bảng tần số ghép nhóm cho dữ liệu ở biểu đồ trên.
b) Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
‒ Sử dụng công thức tính độ lệch chuẩn của mẫu số liệu ghép nhóm: \(S = \sqrt {{S^2}} \).
Lời giải chi tiết
a) Ta có bảng tần số ghép nhóm:

b) Ta có bảng sau:

Cỡ mẫu \(n = 48 + 36 + 18 + 12 + 6 = 120\)
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{48.7,5 + 36.22,5 + 18.37,5 + 12.52,5 + 6.67,5}}{{120}} = 24\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\({S^2} = \frac{1}{{120}}\left( {{{48.7,5}^2} + {{36.22,5}^2} + {{18.37,5}^2} + {{12.52,5}^2} + {{6.67,5}^2}} \right) - {24^2} = 312,75\)
Độ lệch chuẩn của mẫu số liệu ghép nhóm là: \(S = \sqrt {312,75} \approx 17,68\).
Giải bài 4 trang 104 SBT Toán 12 Chân trời sáng tạo: Tổng quan
Bài 4 trang 104 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào chủ đề về Đường thẳng và mặt phẳng trong không gian. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về vectơ chỉ phương, vectơ pháp tuyến, phương trình đường thẳng và mặt phẳng để giải quyết các bài toán liên quan đến vị trí tương đối giữa đường thẳng và mặt phẳng, khoảng cách từ điểm đến mặt phẳng, và các bài toán ứng dụng thực tế.
Nội dung bài 4 trang 104 SBT Toán 12 Chân trời sáng tạo
Bài 4 thường bao gồm các dạng bài tập sau:
- Xác định vị trí tương đối giữa đường thẳng và mặt phẳng: Kiểm tra xem đường thẳng có nằm trong mặt phẳng, song song với mặt phẳng, cắt mặt phẳng hay không.
- Tính góc giữa đường thẳng và mặt phẳng: Sử dụng công thức tính góc giữa đường thẳng và mặt phẳng dựa trên vectơ chỉ phương của đường thẳng và vectơ pháp tuyến của mặt phẳng.
- Tính khoảng cách từ điểm đến mặt phẳng: Áp dụng công thức tính khoảng cách từ điểm đến mặt phẳng.
- Tìm giao điểm của đường thẳng và mặt phẳng: Giải hệ phương trình để tìm tọa độ giao điểm.
- Bài toán ứng dụng: Các bài toán liên quan đến việc xác định vị trí của các vật thể trong không gian.
Lời giải chi tiết bài 4 trang 104 SBT Toán 12 Chân trời sáng tạo
Để giúp các bạn học sinh giải bài tập một cách hiệu quả, Tusach.vn xin trình bày lời giải chi tiết cho từng phần của bài 4:
Ví dụ minh họa (Giả sử bài 4 có 2 phần a và b)
Phần a:
Đề bài: (Ví dụ) Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 3 + 2t và mặt phẳng (P): 2x - y + z - 5 = 0. Xác định vị trí tương đối giữa đường thẳng d và mặt phẳng (P).
Lời giải:
- Tìm vectơ chỉ phương của đường thẳng d:a = (1, -1, 2)
- Tìm vectơ pháp tuyến của mặt phẳng (P):n = (2, -1, 1)
- Tính tích vô hướng a.n:a.n = 1*2 + (-1)*(-1) + 2*1 = 5
- Kết luận: Vì a.n ≠ 0, đường thẳng d và mặt phẳng (P) cắt nhau.
Phần b:
Đề bài: (Ví dụ) Tính khoảng cách từ điểm A(1, 2, 3) đến mặt phẳng (P): 2x - y + z - 5 = 0.
Lời giải:
Sử dụng công thức tính khoảng cách từ điểm A(x0, y0, z0) đến mặt phẳng (P): Ax + By + Cz + D = 0 là:
d(A, (P)) = |Ax0 + By0 + Cz0 + D| / √(A2 + B2 + C2)
Thay số vào, ta có:
d(A, (P)) = |2*1 - 1*2 + 1*3 - 5| / √(22 + (-1)2 + 12) = |2 - 2 + 3 - 5| / √6 = 2 / √6 = √6 / 3
Mẹo giải bài tập về Đường thẳng và mặt phẳng trong không gian
- Nắm vững các công thức tính góc, khoảng cách.
- Vẽ hình minh họa để dễ hình dung bài toán.
- Sử dụng các tính chất của vectơ để đơn giản hóa bài toán.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn luôn cập nhật lời giải chi tiết, chính xác và dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 12 Chân trời sáng tạo. Hãy truy cập tusach.vn để học Toán 12 hiệu quả hơn!