Giải bài 7 trang 34 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 7 trang 34 Sách bài tập Toán 12 - Chân trời sáng tạo
Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho các bài tập trong sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ giúp bạn hiểu rõ cách giải bài 7 trang 34, đồng thời cung cấp kiến thức nền tảng cần thiết để giải quyết các bài toán tương tự.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả và dễ hiểu nhất cho các em học sinh.
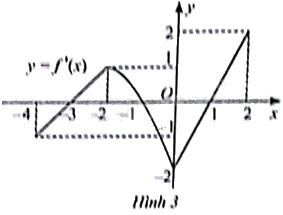
Đồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 3. Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng A. \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;2} \right)\). B. \(\left( { - 2;0} \right)\). C. \(\left( { - 4; - 3} \right)\) và \(\left( { - 1;2} \right)\). D. \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\).
Đề bài
Đồ thị đạo hàm \(f'\left( x \right)\) của hàm số \(y = f\left( x \right)\) được cho trong Hình 3.
Hàm số \(y = f\left( x \right)\) đồng biến trên các khoảng
A. \(\left( { - 4; - 2} \right)\) và \(\left( { - 2;2} \right)\).
B. \(\left( { - 2;0} \right)\).
C. \(\left( { - 4; - 3} \right)\) và \(\left( { - 1;2} \right)\).
D. \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\).
Phương pháp giải - Xem chi tiết
Từ đồ thị hàm số \(y = f'\left( x \right)\), lập bảng biến thiên của hàm số \(y = f\left( x \right)\) rồi xác định tính đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
Ta có: \(y' = 0\) khi \(x = - 1;x = - 3\) hoặc \(x = 1\).
Bảng xét dấu đạo hàm của hàm số:

Dựa vào bảng xét dấu đạo hàm ta có: Hàm số đồng biến trên các khoảng \(\left( { - 3; - 1} \right)\) và \(\left( {1;2} \right)\).
Chọn D.
Giải bài 7 trang 34 Sách bài tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 7 trang 34 Sách bài tập Toán 12 Chân trời sáng tạo thường thuộc chương trình học về đạo hàm, cụ thể là các ứng dụng của đạo hàm trong việc khảo sát hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
- Kiến thức về đạo hàm: Định nghĩa đạo hàm, các quy tắc tính đạo hàm (đạo hàm của tổng, hiệu, tích, thương, hàm hợp), đạo hàm của các hàm số cơ bản (hàm đa thức, hàm lượng giác, hàm mũ, hàm logarit).
- Ứng dụng của đạo hàm: Xác định khoảng đồng biến, nghịch biến của hàm số, tìm cực trị của hàm số, vẽ đồ thị hàm số.
- Kỹ năng giải toán: Phân tích đề bài, lựa chọn phương pháp giải phù hợp, trình bày lời giải rõ ràng, logic.
Nội dung chi tiết bài 7 trang 34
Bài 7 thường yêu cầu học sinh thực hiện một trong các nhiệm vụ sau:
- Khảo sát hàm số: Xác định tập xác định, các điểm gián đoạn, giới hạn vô cùng, đạo hàm bậc nhất, đạo hàm bậc hai, các điểm cực trị, khoảng đồng biến, nghịch biến, điểm uốn, đường tiệm cận.
- Vẽ đồ thị hàm số: Dựa vào kết quả khảo sát hàm số để vẽ đồ thị hàm số.
- Giải phương trình, bất phương trình: Sử dụng đạo hàm để giải phương trình, bất phương trình chứa hàm số.
- Ứng dụng đạo hàm vào các bài toán thực tế: Giải các bài toán tối ưu hóa, bài toán liên quan đến tốc độ biến thiên.
Ví dụ minh họa giải bài 7 trang 34 (Giả định)
Đề bài: Cho hàm số y = x3 - 3x2 + 2. Khảo sát hàm số và vẽ đồ thị.
Lời giải:
- Tập xác định: D = R
- Đạo hàm bậc nhất: y' = 3x2 - 6x
- Tìm cực trị: y' = 0 ⇔ 3x2 - 6x = 0 ⇔ x = 0 hoặc x = 2.
- Xác định khoảng đồng biến, nghịch biến:
- y' > 0 khi x < 0 hoặc x > 2, hàm số đồng biến trên các khoảng (-∞; 0) và (2; +∞).
- y' < 0 khi 0 < x < 2, hàm số nghịch biến trên khoảng (0; 2).
- Điểm cực trị:
- Điểm cực đại: (0; 2)
- Điểm cực tiểu: (2; -2)
- Đạo hàm bậc hai: y'' = 6x - 6
- Điểm uốn: y'' = 0 ⇔ x = 1. Điểm uốn: (1; 0)
- Vẽ đồ thị: Dựa vào các kết quả trên, ta có thể vẽ được đồ thị hàm số.
Mẹo giải bài tập đạo hàm hiệu quả
Để giải các bài tập về đạo hàm một cách hiệu quả, bạn nên:
- Nắm vững các định nghĩa, quy tắc tính đạo hàm.
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị.
- Kiểm tra lại kết quả sau khi giải xong.
Tusach.vn – Đồng hành cùng bạn trên con đường học tập
Tusach.vn luôn cập nhật lời giải chi tiết và chính xác cho các bài tập trong sách giáo khoa và sách bài tập Toán 12 Chân trời sáng tạo. Hãy truy cập tusach.vn để tìm kiếm lời giải cho các bài tập khác và nâng cao kiến thức của bạn!
| Chương | Bài | Liên kết |
|---|---|---|
| 1 | 1 | Giải bài 1 trang 10 |
| 1 | 2 | Giải bài 2 trang 10 |