Giải bài 1 trang 16 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 1 trang 16 SBT Toán 12 Chân trời sáng tạo
Tusach.vn cung cấp lời giải chi tiết và dễ hiểu bài 1 trang 16 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, chuẩn bị tốt cho các kỳ thi sắp tới.
Chúng tôi luôn cập nhật đáp án nhanh nhất và chính xác nhất, đồng thời cung cấp các phương pháp giải bài tập hiệu quả.
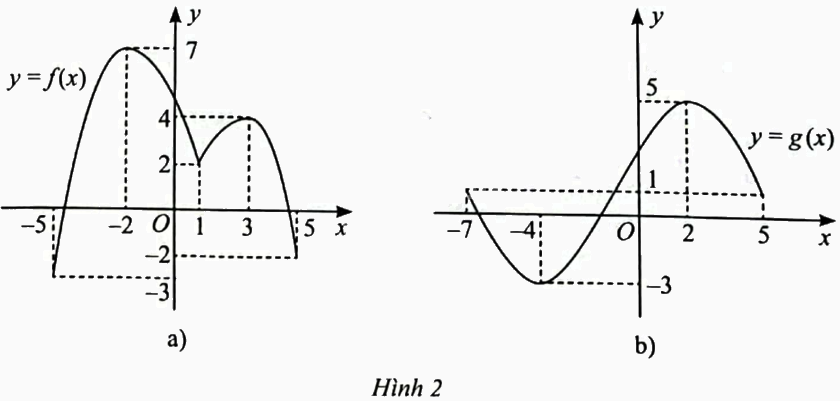
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.
Đề bài
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đồ thị được cho ở Hình 2.
Phương pháp giải - Xem chi tiết
Dựa vào đồ thị hàm số.
Lời giải chi tiết
Dựa vào đồ thị ta có:
a) \(\mathop {\max }\limits_{\left[ { - 5;5} \right]} f\left( x \right) = f\left( { - 2} \right) = 7,\mathop {\min }\limits_{\left[ { - 5;5} \right]} f\left( x \right) = f\left( { - 5} \right) = - 3\);
b) \(\mathop {\max }\limits_{\left[ { - 7;5} \right]} g\left( x \right) = g\left( 2 \right) = 5,\mathop {\min }\limits_{\left[ { - 7;5} \right]} g\left( x \right) = g\left( { - 4} \right) = - 3\).
Giải bài 1 trang 16 SBT Toán 12 Chân trời sáng tạo: Chi tiết và Dễ Hiểu
Bài 1 trang 16 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng, và các yếu tố ảnh hưởng đến hình dạng của parabol để giải quyết các bài toán thực tế.
Nội dung bài 1 trang 16 SBT Toán 12 Chân trời sáng tạo
Bài 1 thường bao gồm các dạng bài tập sau:
- Xác định các yếu tố của parabol: Tìm tọa độ đỉnh, trục đối xứng, hệ số a, và điểm cắt trục tung của parabol.
- Viết phương trình parabol: Xác định phương trình parabol khi biết các yếu tố như đỉnh, trục đối xứng, hoặc các điểm thuộc parabol.
- Tìm điều kiện để parabol có tính chất nhất định: Ví dụ, tìm điều kiện để parabol cắt trục hoành, tiếp xúc với trục hoành, hoặc không cắt trục hoành.
- Ứng dụng parabol vào giải quyết bài toán thực tế: Ví dụ, tìm quỹ đạo của một vật được ném lên theo parabol.
Hướng dẫn giải chi tiết bài 1 trang 16 SBT Toán 12 Chân trời sáng tạo
Để giải bài 1 trang 16 SBT Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
- Công thức tính tọa độ đỉnh của parabol: xđỉnh = -b/(2a), yđỉnh = (4ac - b2)/(4a)
- Phương trình trục đối xứng của parabol: x = -b/(2a)
- Điều kiện để parabol cắt trục hoành: Δ > 0 (với Δ = b2 - 4ac)
- Điều kiện để parabol tiếp xúc với trục hoành: Δ = 0
- Điều kiện để parabol không cắt trục hoành: Δ < 0
Ví dụ minh họa
Bài toán: Tìm tọa độ đỉnh và trục đối xứng của parabol y = x2 - 4x + 3.
Giải:
- Hệ số a = 1, b = -4, c = 3
- Tọa độ đỉnh: xđỉnh = -(-4)/(2*1) = 2, yđỉnh = (4*1*3 - (-4)2)/(4*1) = -1
- Trục đối xứng: x = 2
Lưu ý khi giải bài tập
Khi giải bài tập về parabol, bạn cần chú ý:
- Xác định đúng các hệ số a, b, c của phương trình parabol.
- Sử dụng đúng công thức để tính toán các yếu tố của parabol.
- Kiểm tra lại kết quả để đảm bảo tính chính xác.
- Vận dụng linh hoạt các kiến thức đã học để giải quyết các bài toán khác nhau.
Tusach.vn – Đồng hành cùng bạn học Toán 12
Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập môn Toán 12. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết, và các phương pháp giải bài tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chương | Bài | Link |
|---|---|---|
| 1 | Bài 1 | Giải bài 1 trang 16 |
| 1 | Bài 2 | Giải bài 2 trang 16 |