Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 7 trang 60 sách bài tập toán 12 - Chân trời sáng tạo
SBT Toán 12 - Chân trời sáng tạo
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Chương 5. Phương trình mặt phẳng, đường thẳng, mặt cầu
Bài 3. Phương trình mặt cầu

Giải bài 7 trang 60 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 7 trang 60 SBT Toán 12 Chân trời sáng tạo

Tusach.vn cung cấp lời giải chi tiết và dễ hiểu bài 7 trang 60 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này giúp học sinh nắm vững kiến thức, rèn luyện kỹ năng giải toán và đạt kết quả tốt trong học tập.

Chúng tôi luôn cập nhật đáp án nhanh chóng và chính xác nhất, đồng thời cung cấp các phương pháp giải bài tập hiệu quả.

Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\). a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính kho

Đề bài

Một khu vực đã được thiết lập một hệ toạ độ \(Oxyz\) (đơn vị trên các trục là mét). Một flycam đang phát sóng wifi bao phủ một vùng không gian bên trong mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\). Một người đang sử dụng máy tính tại điểm \(M\) nằm trên điểm giao của mặt cầu \(\left( S \right)\) và mặt đất \(\left( P \right):z = 0\).

a) Xác định toạ độ tâm \(I\) và bán kính của mặt cầu \(\left( S \right)\). Tính khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\).

b) Tính độ dài đoạn thẳng \(JM\). Làm tròn kết quả đến hàng phần trăm của mét.

Phương pháp giải - Xem chi tiếtGiải bài 7 trang 60 sách bài tập toán 12 - Chân trời sáng tạo 1

‒ Mặt cầu \(\left( S \right):{\left( {x - a} \right)^2} + {\left( {y - b} \right)^2} + {\left( {z - c} \right)^2} = {R^2}\) có tâm \(I\left( {a;b;c} \right)\) bán kính \(R\).

‒ Khoảng cách \(IJ\) của đoạn vuông góc từ \(I\) đến \(\left( P \right)\) chính là khoảng cách từ \(I\) đến \(\left( P \right)\).

‒ Khoảng cách từ điểm \({M_0}\left( {{x_0};{y_0};{z_0}} \right)\) đến mặt phẳng \(\left( P \right):Ax + By + C{\rm{z}} + D = 0\):

\(d\left( {{M_0};\left( P \right)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{{\rm{z}}_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Lời giải chi tiết

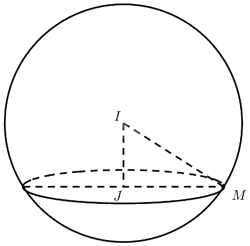
Giải bài 7 trang 60 sách bài tập toán 12 - Chân trời sáng tạo 2

a) Mặt cầu \(\left( S \right):{\left( {x - 20} \right)^2} + {\left( {y - 30} \right)^2} + {\left( {z - 10} \right)^2} = 400\) có tâm \(I\left( {20;30;10} \right)\) bán kính \(R = \sqrt {400} = 20\).

\(IJ = d\left( {I;\left( P \right)} \right) = \frac{{\left| {10} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = 10\left( m \right)\).

b) Ta có \(M \in \left( S \right)\) nên \(IM = R = 20\).

Tam giác \(IJM\) vuông tại \(J\) nên ta có:

\(JM = \sqrt {I{M^2} - I{J^2}} = \sqrt {{{20}^2} - {{10}^2}} = 10\sqrt 3 \approx 17,32\left( m \right)\).

Giải bài 7 trang 60 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp

Bài 7 trang 60 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học kỳ 1 lớp 12, tập trung vào chủ đề về Đạo hàm của hàm số hợp. Đây là một phần kiến thức quan trọng, giúp học sinh hiểu rõ hơn về các quy tắc tính đạo hàm và ứng dụng chúng vào giải quyết các bài toán thực tế.

Nội dung bài 7 trang 60 SBT Toán 12 Chân trời sáng tạo

Bài 7 thường bao gồm các dạng bài tập sau:

  • Tính đạo hàm của hàm số hợp: Yêu cầu học sinh áp dụng quy tắc đạo hàm của hàm hợp để tính đạo hàm của các hàm số phức tạp.
  • Tìm đạo hàm cấp hai: Đòi hỏi học sinh phải tính đạo hàm bậc nhất trước, sau đó tiếp tục tính đạo hàm của đạo hàm bậc nhất để tìm đạo hàm cấp hai.
  • Ứng dụng đạo hàm để giải quyết các bài toán liên quan đến cực trị và khoảng đơn điệu: Bài tập này yêu cầu học sinh sử dụng đạo hàm để xác định các điểm cực trị, khoảng đồng biến, nghịch biến của hàm số.

Lời giải chi tiết bài 7 trang 60 SBT Toán 12 Chân trời sáng tạo

Dưới đây là lời giải chi tiết cho từng phần của bài 7 trang 60 SBT Toán 12 Chân trời sáng tạo:

Bài 7.1

Đề bài: Tính đạo hàm của hàm số y = sin(x2 + 1)

Lời giải:

Sử dụng quy tắc đạo hàm của hàm hợp: y' = u'(x) * v'(u(x))

Đặt u(x) = x2 + 1 và v(u) = sin(u)

Khi đó, u'(x) = 2x và v'(u) = cos(u)

Vậy, y' = 2x * cos(x2 + 1)

Bài 7.2

Đề bài: Tính đạo hàm của hàm số y = ecos(x)

Lời giải:

Sử dụng quy tắc đạo hàm của hàm hợp: y' = u'(x) * v'(u(x))

Đặt u(x) = cos(x) và v(u) = eu

Khi đó, u'(x) = -sin(x) và v'(u) = eu

Vậy, y' = -sin(x) * ecos(x)

Mẹo giải bài tập về đạo hàm hàm số hợp

Để giải tốt các bài tập về đạo hàm hàm số hợp, bạn nên:

  • Nắm vững quy tắc đạo hàm của hàm hợp: Đây là nền tảng để giải quyết mọi bài toán liên quan.
  • Phân tích cấu trúc hàm số: Xác định rõ hàm số ngoài và hàm số trong để áp dụng quy tắc một cách chính xác.
  • Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và làm quen với các dạng bài tập thường gặp.

Tusach.vn – Đồng hành cùng bạn trên con đường học tập

Tusach.vn luôn đồng hành cùng bạn trong quá trình học tập môn Toán. Chúng tôi cung cấp đầy đủ các tài liệu học tập, bài giải chi tiết và các phương pháp giải bài tập hiệu quả. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!

Chủ đềLiên kết
Giải bài tập Toán 12 Chân trời sáng tạohttps://tusach.vn/toan-12-chan-troi-sang-tao
Đạo hàmhttps://tusach.vn/dao-ham

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN