Giải bài 6 trang 46 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 6 trang 46 SBT Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 6 trang 46 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và dễ hiểu, giúp bạn nắm vững kiến thức và tự tin làm bài tập.
Tusach.vn luôn đồng hành cùng bạn trên con đường chinh phục môn Toán.
Cho hình hộp chữ nhật (ABCD.A'B'C'D') có (DA = 2,DC = 3,DD = 2). Tính khoảng cách từ đỉnh (B') đến mặt phẳng (left( {BA'C'} right)).
Đề bài
Cho hình hộp chữ nhật \(ABCD.A'B'C'D'\) có \(DA = 2,DC = 3,DD = 2\).
Tính khoảng cách từ đỉnh \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\).
Phương pháp giải - Xem chi tiết
Gắn vào hệ trục toạ độ và sử dụng công thức tính khoảng cách từ một điểm đến một mặt phẳng.
Lời giải chi tiết
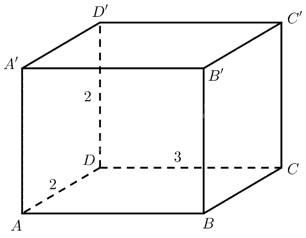
Vì \(ABCD.A'B'C'D'\) là hình hộp chữ nhật nên các đường thẳng \(DA,DC,DD'\) đôi một vuông góc.
Do đó ta có thể gắn hệ trục toạ độ \(Oxyz\) thoả mãn \(D\left( {0;0;0} \right),A\left( {2;0;0} \right),C\left( {0;3;0} \right),D'\left( {0;0;2} \right)\).
Khi đó \(B\left( {2;3;0} \right),B'\left( {2;3;2} \right),A'\left( {2;0;2} \right),C'\left( {0;3;2} \right)\).
Ta có: \(\overrightarrow {BA'} = \left( {0; - 3;2} \right),\overrightarrow {BC'} = \left( { - 2;0;2} \right)\).
Khi đó, \(\left[ {\overrightarrow {BA'} ,\overrightarrow {BC'} } \right] = \left( {\left( { - 3} \right).2 - 2.0;2.\left( { - 2} \right) - 0.2;0.0 - \left( { - 3} \right).\left( { - 2} \right)} \right) = \left( { - 6; - 4; - 6} \right)\) là vectơ pháp tuyến của mặt phẳng \(\left( {BA'C'} \right)\).
Phương trình mặt phẳng \(\left( {BA'C'} \right)\) là:
\( - 6\left( {x - 2} \right) - 4\left( {y - 3} \right) - 6\left( {z - 0} \right) = 0 \Leftrightarrow - 6x - 4y - 6{\rm{z}} + 24 = 0 \Leftrightarrow 3{\rm{x}} + 2y + 3{\rm{z}} - 12 = 0\).
Khi đó khoảng cách từ điểm \(B'\) đến mặt phẳng \(\left( {BA'C'} \right)\) bằng:
\(d\left( {B',\left( {BA'C'} \right)} \right) = \frac{{\left| {3.2 + 2.3 + 3.2 - 12} \right|}}{{\sqrt {{3^2} + {2^2} + {3^2}} }} = \frac{{3\sqrt {22} }}{{11}}\).
Giải bài 6 trang 46 SBT Toán 12 Chân trời sáng tạo: Tổng quan
Bài 6 trang 46 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học kỳ 1 lớp 12, tập trung vào chủ đề về Đạo hàm của hàm số hợp. Bài tập này yêu cầu học sinh vận dụng kiến thức về quy tắc đạo hàm, đặc biệt là quy tắc đạo hàm của hàm hợp, để tính đạo hàm của các hàm số phức tạp. Việc nắm vững quy tắc này là vô cùng quan trọng, không chỉ cho việc giải bài tập trong sách bài tập mà còn cho các bài kiểm tra và thi cử sắp tới.
Nội dung chi tiết bài 6 trang 46 SBT Toán 12 Chân trời sáng tạo
Bài 6 bao gồm các câu hỏi trắc nghiệm và bài tập tự luận, yêu cầu học sinh:
- Tính đạo hàm của các hàm số hợp sử dụng quy tắc đạo hàm.
- Xác định hàm số bên trong và hàm số bên ngoài trong hàm hợp.
- Áp dụng quy tắc đạo hàm một cách linh hoạt để giải quyết các bài toán khác nhau.
Lời giải chi tiết bài 6 trang 46 SBT Toán 12 Chân trời sáng tạo
Câu 1: (Trích dẫn câu 1 và lời giải chi tiết)
Ví dụ: Cho hàm số y = sin(x2 + 1). Tính y'.
Lời giải:
Đặt u = x2 + 1. Khi đó y = sin(u).
Ta có: du/dx = 2x và dy/du = cos(u).
Áp dụng quy tắc đạo hàm của hàm hợp: dy/dx = (dy/du) * (du/dx) = cos(u) * 2x = cos(x2 + 1) * 2x = 2xcos(x2 + 1).
Câu 2: (Trích dẫn câu 2 và lời giải chi tiết)
...
Câu 3: (Trích dẫn câu 3 và lời giải chi tiết)
...
Mẹo giải bài tập về đạo hàm hàm hợp
Để giải quyết hiệu quả các bài tập về đạo hàm hàm hợp, bạn nên:
- Xác định rõ hàm số bên trong và hàm số bên ngoài.
- Nắm vững các công thức đạo hàm cơ bản của các hàm số thường gặp (sin, cos, tan, ln, ex, v.v.).
- Luyện tập thường xuyên để làm quen với các dạng bài tập khác nhau.
- Kiểm tra lại kết quả sau khi tính toán để đảm bảo tính chính xác.
Tài liệu tham khảo hữu ích
Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để nâng cao kiến thức về đạo hàm:
- Sách giáo khoa Toán 12
- Các trang web học Toán trực tuyến uy tín (ví dụ: tusach.vn, VietJack, v.v.)
- Các video bài giảng về đạo hàm trên YouTube
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã hiểu rõ cách giải bài 6 trang 46 sách bài tập Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!
Đừng quên truy cập tusach.vn để xem thêm nhiều bài giải Toán 12 khác và các tài liệu học tập hữu ích.