Giải bài 2 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 2 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 2 trang 36 sách bài tập Toán 12 Chân trời sáng tạo. Tusach.vn cung cấp đáp án chính xác, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin giải các bài tập Toán 12.
Chúng tôi luôn cập nhật nhanh chóng và đầy đủ các bài giải SBT Toán 12 Chân trời sáng tạo, hỗ trợ tối đa cho quá trình học tập của bạn.
Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là \(10l\), Diện tích toàn phần nhỏ nhất của hộp là bao nhiêu?
Đề bài
Người ta muốn làm một chiếc hộp hình hộp chữ nhật có đáy hình vuông và thể tích là \(10l\), Diện tích toàn phần nhỏ nhất của hộp là bao nhiêu?
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính diện tích toàn phần hình hộp chữ nhật để tính diện tích toàn phần \(S\left( x \right)\), sau đó tìm giá trị nhỏ nhất của hàm số \(S\left( x \right)\).
Lời giải chi tiết
Giả sử cạnh của hộp là: \({\rm{x}}\left( {dm} \right)\), chiều cao của hộp là: \({\rm{h}}\left( {dm} \right)\).
Thể tích của hộp là: \(V = {x^2}.h = 10 \Leftrightarrow h = \frac{{10}}{{{x^2}}}\).
Diện tích toàn phần của hình hộp là \(S = 2{{\rm{x}}^2} + 4{\rm{x}}.h = 2{{\rm{x}}^2} + 4{\rm{x}}.\frac{{10}}{{{x^2}}} = 2{{\rm{x}}^2} + \frac{{40}}{x}\left( {d{m^2}} \right)\)
Xét hàm số \(S\left( x \right) = 2{{\rm{x}}^2} + \frac{{40}}{x}\) trên khoảng \(\left( {0; + \infty } \right)\).
Ta có: \(S'\left( x \right) = 4{\rm{x}} - \frac{{40}}{{{x^2}}};S'\left( x \right) = 0 \Leftrightarrow x = \sqrt[3]{{10}}\).
Bảng biến thiên:
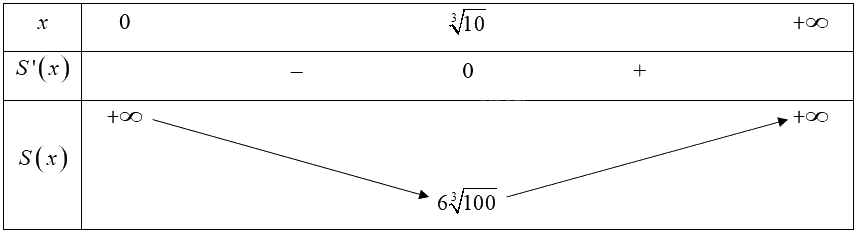
\(V\left( 0 \right) = 0;V\left( 2 \right) = 128;V\left( 6 \right) = 0\)
Vậy \(\mathop {\max }\limits_{\left[ {0;6} \right]} V\left( x \right) = V\left( 2 \right) = 128\).
Vậy với \(x = 2\left( {cm} \right)\) thì thể tích của hình hộp là lớn nhất.
Giải bài 2 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp giải
Bài 2 trang 36 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc rèn luyện kỹ năng giải các bài toán liên quan đến đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức nền tảng và phương pháp giải là yếu tố then chốt để đạt kết quả tốt trong các bài kiểm tra và kỳ thi quan trọng.
Nội dung bài 2 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo
Bài 2 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tìm đạo hàm của hàm số.
- Dạng 2: Khảo sát hàm số bằng đạo hàm (xác định khoảng đồng biến, nghịch biến, cực trị, điểm uốn).
- Dạng 3: Giải các bài toán thực tế liên quan đến ứng dụng của đạo hàm (ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số).
Lời giải chi tiết bài 2 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 2 trang 36, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Câu a: (Ví dụ minh họa)
Cho hàm số y = x3 - 3x2 + 2. Hãy tìm đạo hàm của hàm số.
Lời giải:
y' = 3x2 - 6x
Câu b: (Ví dụ minh họa)
Khảo sát hàm số y = x3 - 3x2 + 2.
Lời giải:
- Xác định tập xác định: Hàm số xác định trên R.
- Tính đạo hàm: y' = 3x2 - 6x
- Tìm điểm cực trị: Giải phương trình y' = 0, ta được x = 0 và x = 2.
- Lập bảng biến thiên: Dựa vào dấu của y' để xác định khoảng đồng biến, nghịch biến và cực trị.
- Kết luận: Hàm số đạt cực đại tại x = 0, giá trị cực đại là y = 2. Hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là y = -2.
Mẹo giải bài tập Toán 12 Chân trời sáng tạo hiệu quả
Để giải bài tập Toán 12 Chân trời sáng tạo một cách hiệu quả, bạn nên:
- Nắm vững kiến thức lý thuyết về đạo hàm và ứng dụng của đạo hàm.
- Luyện tập thường xuyên các bài tập khác nhau để làm quen với các dạng bài và rèn luyện kỹ năng giải.
- Sử dụng các công cụ hỗ trợ như máy tính bỏ túi, phần mềm vẽ đồ thị để kiểm tra lại kết quả.
- Tham khảo các lời giải chi tiết trên tusach.vn để hiểu rõ hơn về phương pháp giải.
Tại sao nên chọn tusach.vn để giải bài tập Toán 12?
Tusach.vn là địa chỉ tin cậy cho các bạn học sinh cần tìm kiếm lời giải bài tập Toán 12 Chân trời sáng tạo. Chúng tôi cam kết:
- Cung cấp lời giải chính xác, dễ hiểu.
- Cập nhật nhanh chóng các bài giải mới nhất.
- Giao diện thân thiện, dễ sử dụng.
- Hỗ trợ nhiệt tình, chu đáo.
Hãy truy cập tusach.vn ngay hôm nay để khám phá thêm nhiều tài liệu học tập hữu ích khác!