Giải bài 11 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 11 trang 11 SBT Toán 12 Chân trời sáng tạo
Chào mừng các em học sinh đến với lời giải chi tiết bài 11 trang 11 sách bài tập Toán 12 Chân trời sáng tạo. Bài viết này sẽ cung cấp đáp án chính xác và phương pháp giải bài tập một cách dễ hiểu nhất.
Tusach.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức \(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\). Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên?
Đề bài
Độ cao (tính bằng mét) của tàu lượn siêu tốc so với mặt đất sau \(t\)(giây) \(\left( {0 \le t \le 20} \right)\) từ lúc bắt đầu được cho bởi công thức
\(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\).
Trong khoảng thời gian nào tàu lượn đi xuống, trong khoảng thời gian nào tàu lượn đi lên?
Phương pháp giải - Xem chi tiết
Xét hàm số \(h\left( t \right)\) trên đoạn \(\left[ {0;20} \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
Xét hàm số \(h\left( t \right) = - \frac{4}{{255}}{t^3} + \frac{{49}}{{85}}{t^2} - \frac{{98}}{{17}}t + 20\) trên đoạn \(\left[ {0;20} \right]\).
Ta có: \(h'\left( t \right) = - \frac{4}{{85}}{t^2} + \frac{{98}}{{85}}t - \frac{{98}}{{17}};h'\left( t \right) = 0 \Leftrightarrow t = \frac{{35}}{2}\) hoặc \(t = 7\).
Bảng biến thiên:
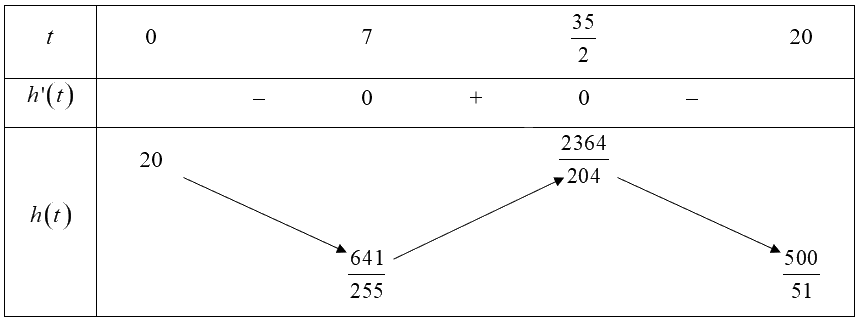
Vậy hàm số đồng biến trên khoảng \(\left( {7;\frac{{35}}{2}} \right)\), hàm số nghịch biến trên các khoảng \(\left( {0;7} \right)\) và \(\left( {\frac{{35}}{2};20} \right)\).
Vậy tàu lượn đi lên trong khoảng thời gian từ 7 giây đến 17,5 giây, tàu lượn đi xuống trong khoảng thời gian từ 0 giây đến 7 giây và từ 17,5 giây đến 20 giây.
Giải bài 11 trang 11 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 11 trang 11 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán lớp 12, tập trung vào việc ôn tập về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, khoảng đơn điệu và vẽ đồ thị hàm số.
Nội dung chi tiết bài 11 trang 11 SBT Toán 12 Chân trời sáng tạo
Bài 11 thường bao gồm các dạng bài tập sau:
- Dạng 1: Tính đạo hàm của hàm số. Yêu cầu tính đạo hàm của các hàm số đơn thức, đa thức, hàm hợp và hàm lượng giác.
- Dạng 2: Tìm cực trị của hàm số. Sử dụng đạo hàm để xác định các điểm cực trị (cực đại, cực tiểu) của hàm số.
- Dạng 3: Khảo sát sự biến thiên của hàm số. Xác định khoảng đồng biến, nghịch biến của hàm số dựa trên dấu của đạo hàm.
- Dạng 4: Ứng dụng đạo hàm để giải các bài toán thực tế. Ví dụ: tìm giá trị lớn nhất, giá trị nhỏ nhất của một đại lượng trong một khoảng cho trước.
Lời giải chi tiết bài 11 trang 11 SBT Toán 12 Chân trời sáng tạo
Dưới đây là lời giải chi tiết cho từng câu hỏi trong bài 11 trang 11 SBT Toán 12 Chân trời sáng tạo:
Câu 1: (Ví dụ minh họa)
Cho hàm số y = x3 - 3x2 + 2. Tìm các điểm cực trị của hàm số.
Lời giải:
- Tính đạo hàm y' = 3x2 - 6x.
- Giải phương trình y' = 0 để tìm các điểm dừng: 3x2 - 6x = 0 => x = 0 hoặc x = 2.
- Khảo sát dấu của y' trên các khoảng (-∞; 0), (0; 2), (2; +∞) để xác định các điểm cực trị.
- Kết luận: Hàm số đạt cực đại tại x = 0, y = 2 và đạt cực tiểu tại x = 2, y = -2.
Câu 2: (Ví dụ minh họa)
Tìm khoảng đồng biến, nghịch biến của hàm số y = x2 - 4x + 3.
Lời giải:
Đạo hàm y' = 2x - 4. Giải phương trình y' = 0 => x = 2. Khảo sát dấu của y' trên các khoảng (-∞; 2) và (2; +∞) để xác định khoảng đồng biến, nghịch biến.
Mẹo giải nhanh và lưu ý quan trọng
- Nắm vững các công thức tính đạo hàm cơ bản.
- Sử dụng bảng xét dấu đạo hàm để xác định các điểm cực trị và khoảng đơn điệu.
- Kiểm tra lại kết quả bằng cách vẽ đồ thị hàm số.
- Luyện tập thường xuyên để nâng cao kỹ năng giải bài tập.
Tusach.vn - Nguồn tài liệu học tập Toán 12 uy tín
Tusach.vn cung cấp đầy đủ lời giải chi tiết, dễ hiểu cho tất cả các bài tập trong sách bài tập Toán 12 Chân trời sáng tạo. Ngoài ra, chúng tôi còn cung cấp các tài liệu ôn tập, đề thi thử và các bài giảng video giúp các em học tập hiệu quả hơn. Hãy truy cập tusach.vn để khám phá thêm nhiều tài liệu hữu ích khác!
| Chương | Bài | Link |
|---|---|---|
| 1 | 1 | Giải bài 1 trang 5 SBT Toán 12 |
| 1 | 2 | Giải bài 2 trang 6 SBT Toán 12 |