Giải bài 6 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 6 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 6 trang 36 Sách bài tập Toán 12 Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn có thể tự tin giải quyết các bài toán tương tự.
Chúng tôi luôn cố gắng mang đến những nội dung chất lượng, giúp bạn học tập hiệu quả và đạt kết quả tốt nhất trong môn Toán.
Nam dùng một tấm bìa có kích thước 50 cm × 20 cm để làm một chiếc lon hình trụ (không có nắp). Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăngtimét thì lon hình trụ đạt thể tích lớn nhất? Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).
Đề bài
Nam dùng một tấm bìa có kích thước 50 cm × 20 cm để làm một chiếc lon hình trụ (không có nắp).
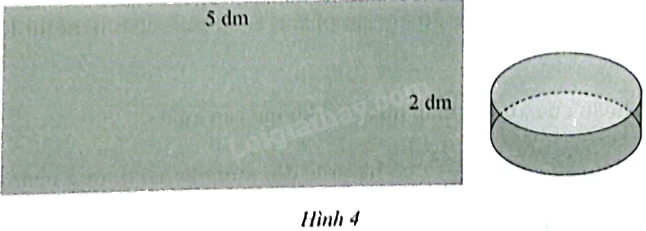
Hỏi cần chọn bán kính đáy hình trụ là bao nhiêu xăngtimét thì lon hình trụ đạt thể tích lớn nhất?
Lưu ý: Kết quả làm tròn đến hàng phần trăm của xăngtimét, bỏ qua phần hao hụt khi cắt và tạo hình, đáy và mặt bên phải là các bìa nguyên vẹn (không ghép nối).
Phương pháp giải - Xem chi tiết
Sử dụng công thức tính thể tích hình trụ để tính thể tích \(V\left( x \right)\), sau đó tìm giá trị lớn nhất của hàm số \(V\left( x \right)\).
Lời giải chi tiết
Gọi \(x\) (dm) là bán kính đáy hình trụ \(\left( {x > 0} \right)\).
• Phương án 1:
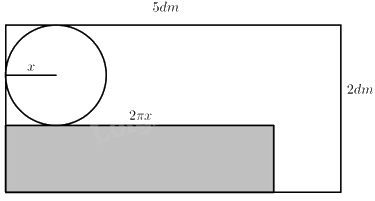
Khi đó chiều cao của hình trụ là: \(2 - 2{\rm{x}}\left( {dm} \right)\).
Chu vi đáy của hình trụ là: \(2\pi {\rm{x}}\left( {dm} \right)\).
Vì chu vi đáy của hình trụ không được vượt quá 5 dm nên ta có: \(2\pi x \le 5 \Leftrightarrow x \le \frac{5}{{2\pi }}\).
Thể tích của hình trụ là: \(V\left( x \right) = \pi {x^2}\left( {2 - 2{\rm{x}}} \right) = - 2\pi {{\rm{x}}^3} + 2\pi {{\rm{x}}^2}\left( {d{m^3}} \right)\).
Xét hàm số \(V\left( x \right) = - 2\pi {{\rm{x}}^3} + 2\pi {{\rm{x}}^2}\) trên nửa khoảng \(\left( {0;\frac{5}{{2\pi }}} \right]\).
Ta có: \(V'\left( x \right) = - 6\pi {{\rm{x}}^2} + 4\pi {\rm{x}}\)
\(V'\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = \frac{2}{3}\).
Bảng biến thiên:
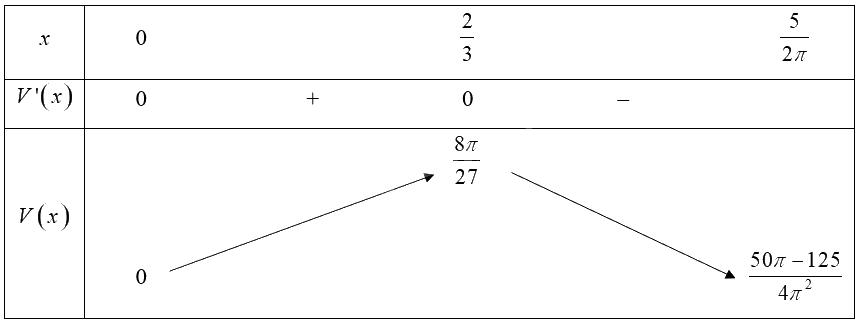
Vậy \(\mathop {\max }\limits_{\left( {0;\frac{5}{{2\pi }}} \right]} V\left( x \right) = V\left( {\frac{2}{3}} \right) = \frac{{8\pi }}{{27}} \approx 0,93\).
Vậy với \(x = \frac{2}{3}\left( {dm} \right)\) thì thể tích của hình trụ là lớn nhất bằng \(0,93\left( {d{m^3}} \right)\).
• Phương án 2:
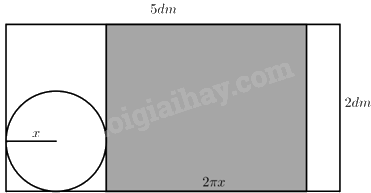
Khi đó chiều cao của hình trụ là: \(2\left( {dm} \right)\).
Chu vi đáy của hình trụ là: \(2\pi {\rm{x}}\left( {dm} \right)\).
Vì tổng đường kính và chu vi đáy của hình trụ không được vượt quá 5 dm nên ta có:
\(2\pi x + 2{\rm{x}} \le 5 \Leftrightarrow 2{\rm{x}}\left( {\pi + 1} \right) \le 5 \Leftrightarrow x \le \frac{5}{{2\left( {\pi + 1} \right)}}\).
Thể tích của hình trụ là: \(V\left( x \right) = \pi {x^2}2 = 2\pi {{\rm{x}}^2}\left( {d{m^3}} \right)\).
Xét hàm số \(V\left( x \right) = 2\pi {{\rm{x}}^2}\) trên nửa khoảng \(\left( {0;\frac{5}{{2\left( {\pi + 1} \right)}}} \right]\).
Ta có: \(V'\left( x \right) = 4\pi {\rm{x}}\)
\(V'\left( x \right) = 0 \Leftrightarrow x = 0\).
Bảng biến thiên:
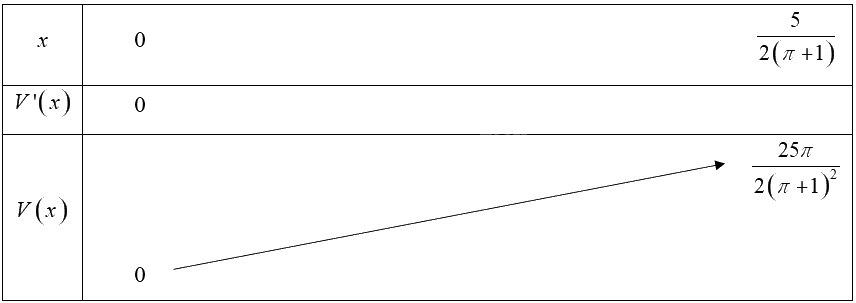
Vậy \(\mathop {\max }\limits_{\left( {0;\frac{5}{{2\pi }}} \right]} V\left( x \right) = V\left( {\frac{5}{{2\left( {\pi + 1} \right)}}} \right) = \frac{{25\pi }}{{2{{\left( {\pi + 1} \right)}^2}}} \approx 2,29\).
Vậy với \(x = \frac{5}{{2\left( {\pi + 1} \right)}}\left( {dm} \right)\) thì thể tích của hình trụ là lớn nhất bằng \(2,29\left( {d{m^3}} \right)\).
Vậy thể tích lon hình trụ lớn nhất khi thiết kế theo phương án 2 và bán kính đáy khoảng \(\frac{5}{{2\left( {\pi + 1} \right)}} \approx 0,60\left( {dm} \right)\).
Giải bài 6 trang 36 Sách bài tập Toán 12 - Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 6 trang 36 Sách bài tập Toán 12 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết bài tập này một cách hiệu quả, trước hết bạn cần nắm vững lý thuyết liên quan, các công thức và định lý quan trọng. Bài tập này thường yêu cầu vận dụng kiến thức đã học vào giải quyết các bài toán thực tế, đòi hỏi sự tư duy logic và khả năng phân tích.
Nội dung chi tiết bài 6 trang 36
Để giúp bạn hiểu rõ hơn về bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài toán. Thông thường, bài 6 sẽ bao gồm một số câu hỏi nhỏ, mỗi câu hỏi yêu cầu một cách tiếp cận khác nhau. Dưới đây là lời giải chi tiết cho từng câu hỏi:
Câu a: (Ví dụ về nội dung câu a)
Đề bài: (Ví dụ về đề bài câu a)
Lời giải: (Ví dụ về lời giải câu a, kèm theo giải thích chi tiết từng bước)
Câu b: (Ví dụ về nội dung câu b)
Đề bài: (Ví dụ về đề bài câu b)
Lời giải: (Ví dụ về lời giải câu b, kèm theo giải thích chi tiết từng bước)
Các dạng bài tập thường gặp trong bài 6
- Dạng 1: Bài tập về (Ví dụ về dạng bài tập 1)
- Dạng 2: Bài tập về (Ví dụ về dạng bài tập 2)
- Dạng 3: Bài tập về (Ví dụ về dạng bài tập 3)
Mẹo giải bài tập Toán 12 Chân trời sáng tạo hiệu quả
- Đọc kỹ đề bài: Hiểu rõ yêu cầu của đề bài là bước đầu tiên quan trọng để giải quyết bài tập thành công.
- Xác định kiến thức cần sử dụng: Xác định các công thức, định lý, lý thuyết liên quan đến bài toán.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo kết quả của bạn là chính xác và hợp lý.
Luyện tập thêm
Để củng cố kiến thức và kỹ năng giải bài tập, bạn nên luyện tập thêm với các bài tập tương tự trong sách bài tập và các đề thi thử. Việc luyện tập thường xuyên sẽ giúp bạn tự tin hơn khi đối mặt với các bài toán khó.
Bảng tổng hợp công thức liên quan
| Công thức | Mô tả |
|---|---|
| (Ví dụ công thức 1) | (Ví dụ mô tả công thức 1) |
| (Ví dụ công thức 2) | (Ví dụ mô tả công thức 2) |
Kết luận
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã có thể tự tin giải bài 6 trang 36 Sách bài tập Toán 12 Chân trời sáng tạo. Đừng ngần ngại đặt câu hỏi nếu bạn gặp bất kỳ khó khăn nào. Chúc bạn học tập tốt!