Đề bài
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) \(y = {x^3} - 8{x^2} - 12x + 1\) trên đoạn \(\left[ { - 2;9} \right]\);
b) \(y = - 2{x^3} + 9{x^2} - 17\) trên nửa khoảng \(\left( { - \infty ;4} \right]\);
c) \(y = {x^3} - 12x + 4\) trên đoạn \(\left[ { - 6;3} \right]\);
d) \(y = 2{x^3} - {x^2} - 28x - 3\) trên đoạn \(\left[ { - 2;1} \right]\);
e) \(y = - 3{x^3} + 4{x^2} - 5x - 17\) trên đoạn \(\left[ { - 1;2} \right]\).
Phương pháp giải - Xem chi tiết
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ {a;b} \right]\):
Bước 1. Tìm các điểm \({x_1},{x_2},...,{x_n}\) thuộc khoảng \(\left( {a;b} \right)\) mà tại đó \(f'\left( x \right)\) bằng 0 hoặc không tồn tại.
Bước 2. Tính \(f\left( a \right);f\left( {{x_1}} \right);f\left( {{x_2}} \right);...;f\left( {{x_n}} \right);f\left( b \right)\).
Bước 3. Gọi \(M\) là số lớn nhất và \(m\) là số nhỏ nhất trong các giá trị tìm được ở Bước 2. Khi đó: \(M = \mathop {\max }\limits_{\left[ {a;b} \right]} f\left( x \right),m = \mathop {\min }\limits_{\left[ {a;b} \right]} f\left( x \right)\).
• Cách tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên một khoảng hay nửa khoảng bằng đạo hàm:
‒ Lập bảng biến thiên của hàm số trên tập hợp đó.
‒ Căn cứ vào bảng biến thiên, kết luận giá trị lớn nhất và giá trị nhỏ nhất (nếu có) của hàm số.
Lời giải chi tiết
a) Xét hàm số \(y = f\left( x \right) = {x^3} - 8{x^2} - 12x + 1\) trên đoạn \(\left[ { - 2;9} \right]\).
Ta có: \(f'\left( x \right) = 3{{\rm{x}}^2} - 16{\rm{x}} - 12\)
\(f'\left( x \right) = 0 \Leftrightarrow x = 6\) hoặc \(x = - \frac{2}{3}\).
\(f\left( { - 2} \right) = - 15;f\left( { - \frac{2}{3}} \right) = \frac{{139}}{{27}};f\left( 6 \right) = - 143;f\left( 9 \right) = - 26\)
Vậy \(\mathop {\max }\limits_{\left[ { - 2;9} \right]} f\left( x \right) = f\left( { - \frac{2}{3}} \right) = \frac{{139}}{{27}},\mathop {\min }\limits_{\left[ { - 2;9} \right]} f\left( x \right) = f\left( 6 \right) = - 143\).
b) Xét hàm số \(y = f\left( x \right) = - 2{x^3} + 9{x^2} - 17\) trên nửa khoảng \(\left( { - \infty ;4} \right]\).
Ta có: \(f'\left( x \right) = - 6{{\rm{x}}^2} + 18{\rm{x}}\)
\(f'\left( x \right) = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\).
Bảng biến thiên của hàm số trên nửa khoảng \(\left( { - \infty ;4} \right]\):
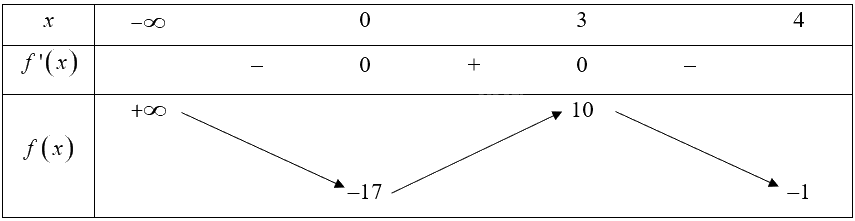
Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{\left( { - \infty ;4} \right]} f\left( x \right) = f\left( 0 \right) = - 17\), hàm số không có giá trị lớn nhất trên nửa khoảng \(\left( { - \infty ;4} \right]\).
c) Xét hàm số \(y = f\left( x \right) = {x^3} - 12x + 4\) trên đoạn \(\left[ { - 6;3} \right]\).
Ta có: \(f'\left( x \right) = 3{{\rm{x}}^2} - 12\)
\(f'\left( x \right) = 0 \Leftrightarrow x = 2\) hoặc \(x = - 2\).
\(f\left( { - 6} \right) = - 140;f\left( { - 2} \right) = 20;f\left( 2 \right) = - 12;f\left( 3 \right) = - 5\)
Vậy \(\mathop {\max }\limits_{\left[ { - 6;3} \right]} f\left( x \right) = f\left( { - 2} \right) = 20,\mathop {\min }\limits_{\left[ { - 6;3} \right]} f\left( x \right) = f\left( { - 6} \right) = - 140\).
d) Xét hàm số \(y = 2{x^3} - {x^2} - 28x - 3\) trên đoạn \(\left[ { - 2;1} \right]\).
Ta có: \(f'\left( x \right) = 6{{\rm{x}}^2} - 2{\rm{x}} - 28\)
\(f'\left( x \right) = 0 \Leftrightarrow x = \frac{7}{3}\) (loại) hoặc \(x = - 2\).
\(f\left( { - 2} \right) = 33;f\left( 1 \right) = - 30\)
Vậy \(\mathop {\max }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = f\left( { - 2} \right) = 33,\mathop {\min }\limits_{\left[ { - 2;1} \right]} f\left( x \right) = f\left( 1 \right) = - 30\).
e) Xét hàm số \(y = f\left( x \right) = - 3{x^3} + 4{x^2} - 5x - 17\) trên đoạn \(\left[ { - 1;2} \right]\).
Ta có: \(f'\left( x \right) = - 9{{\rm{x}}^2} + 8{\rm{x}} - 5 = - 9{\left( {x - \frac{4}{9}} \right)^2} - \frac{{29}}{9} < 0,\forall x \in \left[ { - 1;2} \right]\)
\(f\left( { - 1} \right) = - 5;f\left( 2 \right) = - 35\)
Vậy \(\mathop {\max }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( { - 1} \right) = - 5,\mathop {\min }\limits_{\left[ { - 1;2} \right]} f\left( x \right) = f\left( 2 \right) = - 35\).
