Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
SBT Toán 12 - Chân trời sáng tạo
SBT TOÁN TẬP 1 - CHÂN TRỜI SÁNG TẠO
Chương 1. Ứng dụng đạo hàm để khảo sát hàm số
Bài 1. Tính đơn điệu và cực trị của hàm số

Giải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 9 trang 11 SBT Toán 12 Chân trời sáng tạo

Tusach.vn cung cấp lời giải chi tiết, dễ hiểu bài 9 trang 11 sách bài tập Toán 12 Chân trời sáng tạo. Bài giải được các giáo viên có kinh nghiệm biên soạn, đảm bảo tính chính xác và giúp học sinh nắm vững kiến thức.

Chúng tôi luôn cập nhật nhanh chóng và đầy đủ các bài giải SBT Toán 12 Chân trời sáng tạo, hỗ trợ tối đa cho quá trình học tập của bạn.

Tìm \(m\) để phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt.

Đề bài

Tìm \(m\) để phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt.

Phương pháp giải - Xem chi tiếtGiải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo 1

Xét hàm số \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\), lập bảng biến thiên, xét sự tương giao của đồ thị hàm số với đường thẳng \(y = m\) và kết luận.

Lời giải chi tiết

Đặt \(y = \frac{{{x^2} + x + 4}}{{x + 1}}\).

Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có

\(y' = \frac{{{{\left( {{x^2} + x + 4} \right)}^\prime }\left( {x + 1} \right) - \left( {{x^2} + x + 4} \right){{\left( {x + 1} \right)}^\prime }}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{\left( {2{\rm{x}} + 1} \right)\left( {x + 1} \right) - \left( {{x^2} + x + 4} \right)}}{{{{\left( {x + 1} \right)}^2}}} = \frac{{{x^2} + 2{\rm{x}} - 3}}{{{{\left( {x + 1} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow x = 1\) hoặc \({\rm{x}} = - 3\).

Bảng biến thiên:

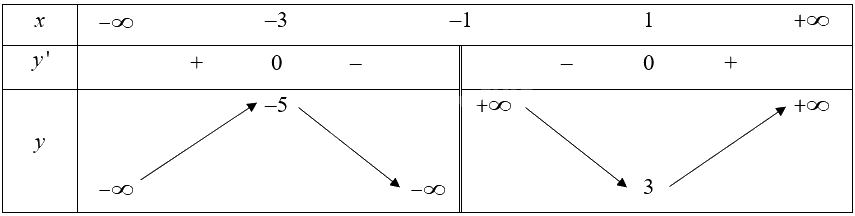
Giải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo 2

Từ bảng biển thiên, ta thấy đường thẳng \(y = m\) giao với đồ thị của hàm số tại hai nghiệm phân biệt khi \(m > 3\) hoặc \(m < - 5\). Do đó phương trình \(\frac{{{x^2} + x + 4}}{{x + 1}} = m\) có hai nghiệm phân biệt khi \(m > 3\) hoặc \(m < - 5\).

Giải bài 9 trang 11 SBT Toán 12 Chân trời sáng tạo: Chi tiết và Dễ Hiểu

Bài 9 trang 11 sách bài tập Toán 12 Chân trời sáng tạo thuộc chương trình học Toán 12, tập trung vào việc ôn tập chương 1: Hàm số bậc hai. Bài tập này thường yêu cầu học sinh vận dụng kiến thức về parabol, đỉnh của parabol, trục đối xứng, và các yếu tố ảnh hưởng đến hình dạng của parabol để giải quyết các bài toán thực tế.

Nội dung chính của bài 9 trang 11 SBT Toán 12 Chân trời sáng tạo

  • Xác định các yếu tố của parabol: a, b, c.
  • Tìm tọa độ đỉnh của parabol.
  • Xác định trục đối xứng của parabol.
  • Tìm khoảng đồng biến, nghịch biến của hàm số.
  • Vẽ đồ thị hàm số.
  • Ứng dụng hàm số bậc hai vào giải quyết các bài toán thực tế.

Phương pháp giải bài tập hàm số bậc hai hiệu quả

  1. Nắm vững lý thuyết: Hiểu rõ các khái niệm, định lý, công thức liên quan đến hàm số bậc hai.
  2. Phân tích đề bài: Xác định rõ yêu cầu của đề bài, các dữ kiện đã cho và các yếu tố cần tìm.
  3. Sử dụng công thức: Áp dụng các công thức phù hợp để tính toán và tìm ra kết quả.
  4. Kiểm tra lại kết quả: Đảm bảo kết quả tính toán chính xác và phù hợp với điều kiện của bài toán.

Ví dụ minh họa giải bài 9 trang 11 SBT Toán 12 Chân trời sáng tạo

Đề bài: Cho hàm số y = x2 - 4x + 3. Tìm tọa độ đỉnh của parabol.

Lời giải:

Hàm số y = x2 - 4x + 3 có dạng y = ax2 + bx + c, với a = 1, b = -4, c = 3.

Tọa độ đỉnh của parabol là:

xđỉnh = -b / (2a) = -(-4) / (2 * 1) = 2

yđỉnh = (2)2 - 4 * (2) + 3 = 4 - 8 + 3 = -1

Vậy tọa độ đỉnh của parabol là (2; -1).

Lưu ý khi giải bài tập hàm số bậc hai

  • Chú ý đến dấu của hệ số a để xác định chiều mở của parabol (lên trên hoặc xuống dưới).
  • Sử dụng máy tính bỏ túi để kiểm tra lại kết quả tính toán.
  • Luyện tập thường xuyên để nắm vững kiến thức và kỹ năng giải bài tập.

Tusach.vn – Nguồn tài liệu học tập Toán 12 uy tín

Tusach.vn là website cung cấp đầy đủ và chính xác các tài liệu học tập Toán 12, bao gồm:

  • Giải bài tập sách giáo khoa
  • Giải bài tập sách bài tập
  • Đề thi thử Toán 12
  • Tài liệu ôn thi THPT Quốc gia

Hãy truy cập tusach.vn để có thêm nhiều tài liệu hữu ích và hỗ trợ cho quá trình học tập của bạn!

Bảng tổng hợp các bài giải SBT Toán 12 Chân trời sáng tạo

TrangBàiLiên kết
111Giải bài 1 trang 11
112Giải bài 2 trang 11
119Giải bài 9 trang 11

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN