Logo
  1. Trang Chủ
  2. Tài Liệu Học Tập
  3. Giải bài 8 trang 22 sách bài tập toán 12 - Chân trời sáng tạo
SBT Toán 12 - Chân trời sáng tạo
SBT TOÁN TẬP 2 - CHÂN TRỜI SÁNG TẠO
Chương 4. Nguyên hàm. Tích phân
Bài 3. Ứng dụng hình học của tích phân

Giải bài 8 trang 22 sách bài tập toán 12 - Chân trời sáng tạo

Giải bài 8 trang 22 SBT Toán 12 Chân trời sáng tạo

Chào mừng bạn đến với tusach.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 8 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn, vì vậy chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu nhất.

Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng cần thiết để tự tin giải quyết các bài toán tương tự.

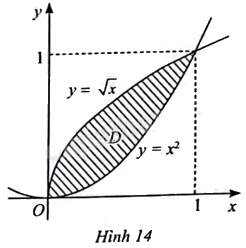
Gọi (D) là hình phẳng giới hạn bởi đồ thị của hai hàm số (y = {x^2}) và (y = sqrt x ) (Hình 14). a) Tính diện tích của (D). b) Tinh thể tích của khối tròn xoay tạo thành khi quay (D) quanh trục (Ox).

Đề bài

Gọi \(D\) là hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2}\) và \(y = \sqrt x \) (Hình 14).

a) Tính diện tích của \(D\).

b) Tinh thể tích của khối tròn xoay tạo thành khi quay \(D\) quanh trục \(Ox\).

Giải bài 8 trang 22 sách bài tập toán 12 - Chân trời sáng tạo 1

Phương pháp giải - Xem chi tiếtGiải bài 8 trang 22 sách bài tập toán 12 - Chân trời sáng tạo 2

‒ Sử dụng công thức: Tính diện tích hình phẳng giới hạn bởi đồ thị của các hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) là: \(S = \int\limits_a^b {\left| {f\left( x \right) - g\left( x \right)} \right|dx} \).

‒ Sử dụng công thức: Tính thể tích khối tròn xoay khi xoay hình phẳng giới hạn bởi đồ thị của hàm số \(y = f\left( x \right),y = g\left( x \right)\) và hai đường thẳng \(x = a,x = b\) quay quanh trục \(Ox\) là: \(V = \pi \int\limits_a^b {\left| {{{\left[ {f\left( x \right)} \right]}^2} - {{\left[ {g\left( x \right)} \right]}^2}} \right|dx} \).

Lời giải chi tiết

a) \(S = \int\limits_0^1 {\left| {\sqrt x - {x^2}} \right|dx} = \int\limits_0^1 {\left( {\sqrt x - {x^2}} \right)dx} = \int\limits_0^1 {\left( {{x^{\frac{1}{2}}} - {x^2}} \right)dx} = \left. {\left( {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 = \frac{1}{3}\).

b) \(V = \pi \int\limits_0^1 {\left| {{{\left( {\sqrt x } \right)}^2} - {{\left( {{x^2}} \right)}^2}} \right|dx} = \pi \int\limits_0^1 {\left| {x - {x^4}} \right|dx} \)

\(x - {x^4} = 0 \Leftrightarrow x = 0\) hoặc \({\rm{x}} = 1\).

\(V = \pi \int\limits_0^1 {\left| {x - {x^4}} \right|dx} = \left| {\pi \int\limits_0^1 {\left( {x - {x^4}} \right)dx} } \right| = \left| {\left. {\pi \left( {\frac{{{x^2}}}{2} - \frac{{{x^5}}}{5}} \right)} \right|_0^1} \right| = \frac{{3\pi }}{{10}}\).

Giải bài 8 trang 22 SBT Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp giải

Bài 8 trang 22 sách bài tập Toán 12 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết bài toán này một cách hiệu quả, bạn cần nắm vững kiến thức lý thuyết liên quan, bao gồm định nghĩa, tính chất, công thức và các định lý quan trọng. Ngoài ra, việc luyện tập thường xuyên với các bài tập tương tự cũng rất cần thiết để củng cố kiến thức và rèn luyện kỹ năng giải toán.

Nội dung chi tiết bài 8 trang 22 SBT Toán 12 Chân trời sáng tạo

Để giúp bạn hiểu rõ hơn về bài toán, chúng ta sẽ cùng nhau phân tích từng phần của đề bài và tìm ra phương pháp giải phù hợp. Thông thường, bài toán sẽ yêu cầu bạn thực hiện một hoặc nhiều thao tác sau:

  • Tính toán giá trị của biểu thức.
  • Giải phương trình hoặc bất phương trình.
  • Chứng minh một đẳng thức hoặc bất đẳng thức.
  • Tìm điều kiện để một bài toán có nghiệm.
  • Vận dụng kiến thức vào thực tế.

Lời giải chi tiết bài 8 trang 22 SBT Toán 12 Chân trời sáng tạo

Dưới đây là lời giải chi tiết cho bài 8 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Chúng tôi sẽ trình bày từng bước giải một cách rõ ràng và dễ hiểu, kèm theo các giải thích chi tiết để bạn có thể nắm bắt được bản chất của bài toán.

(Giả sử đây là một bài toán về đạo hàm và cực trị của hàm số)

Đề bài: Tìm cực trị của hàm số y = x3 - 3x2 + 2

Lời giải:

  1. Tính đạo hàm cấp nhất: y' = 3x2 - 6x
  2. Tìm điểm dừng: Giải phương trình y' = 0, ta được x = 0 hoặc x = 2
  3. Tính đạo hàm cấp hai: y'' = 6x - 6
  4. Xác định cực trị:
    • Tại x = 0, y'' = -6 < 0, hàm số đạt cực đại tại x = 0, ymax = 2
    • Tại x = 2, y'' = 6 > 0, hàm số đạt cực tiểu tại x = 2, ymin = -2

Mẹo giải nhanh và lưu ý quan trọng

Để giải bài toán này một cách nhanh chóng và chính xác, bạn có thể áp dụng một số mẹo sau:

  • Nắm vững các công thức đạo hàm cơ bản.
  • Sử dụng máy tính bỏ túi để tính toán nhanh chóng.
  • Kiểm tra lại kết quả sau khi giải xong.

Lưu ý: Khi giải bài toán về đạo hàm, bạn cần chú ý đến điều kiện xác định của hàm số và các điểm không đạo hàm được.

Bài tập tương tự và luyện tập thêm

Để củng cố kiến thức và kỹ năng giải toán, bạn có thể luyện tập thêm với các bài tập tương tự trong sách bài tập Toán 12 Chân trời sáng tạo. Ngoài ra, bạn cũng có thể tìm kiếm các bài tập trực tuyến trên các trang web học toán uy tín.

Kết luận

Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về cách giải bài 8 trang 22 sách bài tập Toán 12 Chân trời sáng tạo. Nếu bạn có bất kỳ câu hỏi nào, đừng ngần ngại liên hệ với chúng tôi để được hỗ trợ.

Chủ đềNội dung
Đạo hàmCông thức, tính chất, ứng dụng
Cực trịĐiều kiện, phương pháp tìm cực trị
Nguồn: tusach.vn

Tải sách PDF tại TuSach.vn mang đến trải nghiệm tiện lợi và nhanh chóng cho người yêu sách. Với kho sách đa dạng từ sách văn học, sách kinh tế, đến sách học ngoại ngữ, bạn có thể dễ dàng tìm và tải sách miễn phí với chất lượng cao. TuSach.vn cung cấp định dạng sách PDF rõ nét, tương thích nhiều thiết bị, giúp bạn tiếp cận tri thức mọi lúc, mọi nơi. Hãy khám phá kho sách phong phú ngay hôm nay!

CHỦ ĐỀ SÁCH XEM NHIỀU

Sách kỹ năng sống, Sách nuôi dạy con, Sách tiểu sử hồi ký, Sách nữ công gia chánh, Sách học tiếng hàn, Sách thiếu nhi, tài liệu học tập

VỀ TUSACH.VN