Đề bài
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh bằng 4. Mặt bên \(SAB\) là tam giác cân tại \(S\) có chiều cao bằng 6 và nằm trong mặt phẳng vuông góc với đáy.
a) Tính góc \(\alpha \) giữa hai đường thẳng \(SD\) và \(BC\);
b) Tính góc \(\beta \) giữa hai mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SCD} \right)\).
Phương pháp giải - Xem chi tiết
Gắn vào hệ trục toạ độ và sử dụng công thức góc giữa hai đường thẳng và góc giữa hai mặt phẳng.
Lời giải chi tiết
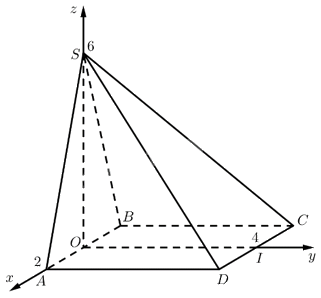
Gọi \(O\) là trung điểm của \(AB\), \(I\) là trung điểm của \(C{\rm{D}}\).
\(SAB\) là tam giác cân tại \(S\) nên \(SO \bot AB\), suy ra \(SO \bot \left( {ABCD} \right)\).
Chọn hệ trục \(Oxyz\) như hình vẽ. Ta có:
\(S\left( {0;0;6} \right),A\left( {2;0;0} \right),B\left( { - 2;0;0} \right),C\left( { - 2;4;0} \right),D\left( {2;4;0} \right)\).
a) Ta có \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {BC} = \left( {0;4;0} \right)\), suy ra
\(\cos \left( {S{\rm{D}},BC} \right) = \left| {\cos \left( {\overrightarrow {S{\rm{D}}} ,\overrightarrow {BC} } \right)} \right| = \frac{{\left| {2.0 + 4.4 + \left( { - 6} \right).0} \right|}}{{\sqrt {{2^2} + {4^2} + {{\left( { - 6} \right)}^2}} .\sqrt {{0^2} + {4^2} + {0^2}} }} = \frac{{\sqrt {14} }}{7}\)
Vậy \(\left( {S{\rm{D}},BC} \right) \approx {57,7^ \circ }\).
b) Ta có: \(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {SA} = \left( {2;0; - 6} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {SA} } \right] = \left( { - 24;0; - 8} \right) = - 8\left( {3;0;1} \right)\).
Do đó \(\left( {SAD} \right)\) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;0;1} \right)\).
\(\overrightarrow {SD} = \left( {2;4; - 6} \right),\overrightarrow {CD} = \left( {4;0;0} \right) \Rightarrow \left[ {\overrightarrow {SD} ,\overrightarrow {CD} } \right] = \left( {0; - 24; - 16} \right) = - 8\left( {0;3;2} \right)\).
Do đó \(\left( {SCD} \right)\) có vectơ pháp tuyến \(\overrightarrow {n'} = \left( {0;3;2} \right)\).
\(\cos \left( {\left( {SAD} \right),\left( {SCD} \right)} \right) = \left| {\cos \left( {\overrightarrow n ,\overrightarrow {n'} } \right)} \right| = \frac{{\left| {3.0 + 0.3 + 1.2} \right|}}{{\sqrt {{3^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {2^2}} }} = \frac{{2\sqrt {130} }}{{130}}\)
Vậy \(\left( {\left( {SAD} \right),\left( {SCD} \right)} \right) \approx {79,9^ \circ }\).
