Giải bài 16 trang 78 sách bài tập toán 12 - Chân trời sáng tạo
Tổng quan nội dung
Giải bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo
Chào mừng bạn đến với lời giải chi tiết bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo trên tusach.vn. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng và những lưu ý quan trọng để bạn có thể tự tin giải quyết các bài toán tương tự.
Chúng tôi hiểu rằng việc học Toán đôi khi có thể gặp nhiều khó khăn. Vì vậy, tusach.vn luôn cố gắng mang đến những tài liệu học tập chất lượng, dễ hiểu và phù hợp với từng đối tượng học sinh.
Chọn đúng hoặc sai cho mỗi ý a, b, c, d. Cho hình lập phương (ABCD.A'B'C'D') có cạnh bằng 2. a) (overrightarrow {AB} = overrightarrow {C'D'} ). b) (overrightarrow {AB} + overrightarrow {DC} = 2overrightarrow {D'C'} ). c) (overrightarrow {AB} + overrightarrow {AD} + overrightarrow {AA'} = overrightarrow {AC'} ). d) (overrightarrow {AC} .overrightarrow {AD'} = 8).
Đề bài
Chọn đúng hoặc sai cho mỗi ý a, b, c, d.Cho hình lập phương \(ABCD.A'B'C'D'\) có cạnh bằng 2. a) \(\overrightarrow {AB} = \overrightarrow {C'D'} \). b) \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {D'C'} \). c) \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \). d) \(\overrightarrow {AC} .\overrightarrow {AD'} = 8\).
Phương pháp giải - Xem chi tiết
‒ Sử dụng quy tắc cộng, quy tắc hình hộp.
‒ Sử dụng tích vô hướng của hai vectơ: \(\cos \left( {\overrightarrow a ,\overrightarrow b } \right) = \frac{{\overrightarrow a .\overrightarrow b }}{{\left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|}}\).
Lời giải chi tiết
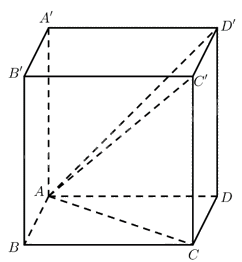
\(ABC'D'\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {D'C'} \). Vậy a) sai.
\(ABCD\) là hình bình hành nên \(\overrightarrow {AB} = \overrightarrow {DC} \).
Do đó \(\overrightarrow {AB} + \overrightarrow {DC} = 2\overrightarrow {DC} = 2\overrightarrow {D'C'} \). Vậy b) đúng.
Theo quy tắc hình hộp ta có: \(\overrightarrow {AB} + \overrightarrow {AD} + \overrightarrow {AA'} = \overrightarrow {AC'} \). Vậy c) đúng.
Xét tam giác \(AC{\rm{D}}'\) có \(AC,A{\rm{D}}',C{\rm{D}}'\) đều là các đường chéo hình vuông. Do đó \(AC = A{\rm{D}}' = C{\rm{D}}' = AB\sqrt 2 = 2\sqrt 2 \).
Vậy tam giác \(AC{\rm{D}}'\) là tam giác đều. Suy ra \(\widehat {CAD'} = {60^ \circ }\)
\(\overrightarrow {AC} .\overrightarrow {AD'} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {AD'} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {AD'} } \right) = AC.AD'.\cos \widehat {CAD'} = 2\sqrt 2 .2\sqrt 2 .\cos {60^ \circ } = 4\).
Vậy d) sai.
a) S.
b) Đ.
c) Đ.
d) S.
Giải bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo: Tổng quan và Phương pháp
Bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo thường tập trung vào một chủ đề cụ thể trong chương trình học. Để giải quyết bài toán này một cách hiệu quả, bạn cần nắm vững kiến thức lý thuyết liên quan, hiểu rõ yêu cầu của đề bài và áp dụng các phương pháp giải phù hợp.
Nội dung chính của bài 16 trang 78 (Ví dụ - cần thay đổi theo nội dung thực tế của bài toán)
Giả sử bài 16 trang 78 yêu cầu tính đạo hàm của hàm số hoặc giải phương trình lượng giác. Để giải quyết, bạn cần:
- Nắm vững các công thức đạo hàm cơ bản: Đạo hàm của hàm số lũy thừa, hàm số lượng giác, hàm số mũ, hàm số logarit,...
- Áp dụng quy tắc đạo hàm: Quy tắc đạo hàm của tổng, hiệu, tích, thương, hàm hợp,...
- Sử dụng các phương pháp giải phương trình lượng giác: Đưa về phương trình cơ bản, sử dụng công thức nghiệm,...
Lời giải chi tiết bài 16 trang 78
Dưới đây là lời giải chi tiết cho từng phần của bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo. (Lưu ý: Nội dung này cần được thay thế bằng lời giải thực tế của bài toán)
Câu a: (Ví dụ - cần thay đổi theo nội dung thực tế của bài toán)
Đề bài: Tính đạo hàm của hàm số f(x) = x3 + 2x2 - 5x + 1.
Lời giải:
f'(x) = 3x2 + 4x - 5
Câu b: (Ví dụ - cần thay đổi theo nội dung thực tế của bài toán)
Đề bài: Giải phương trình sin(x) = 1/2.
Lời giải:
x = π/6 + k2π hoặc x = 5π/6 + k2π, với k là số nguyên.
Mẹo giải nhanh và những lưu ý quan trọng
Để giải bài tập Toán 12 hiệu quả, bạn nên:
- Đọc kỹ đề bài: Xác định rõ yêu cầu của đề bài và các dữ kiện đã cho.
- Lập kế hoạch giải: Xác định các bước cần thực hiện để giải quyết bài toán.
- Kiểm tra lại kết quả: Đảm bảo rằng kết quả của bạn là chính xác và hợp lý.
- Luyện tập thường xuyên: Giải nhiều bài tập khác nhau để rèn luyện kỹ năng và nâng cao kiến thức.
Tài liệu tham khảo hữu ích
Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau:
- Sách giáo khoa Toán 12 Chân trời sáng tạo
- Các trang web học Toán trực tuyến
- Các video bài giảng trên YouTube
Bảng tổng hợp công thức (Ví dụ - cần thay đổi theo nội dung thực tế của bài toán)
| Công thức | Mô tả |
|---|---|
| (u + v)' = u' + v' | Đạo hàm của tổng |
| (u - v)' = u' - v' | Đạo hàm của hiệu |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, bạn đã có thể tự tin giải quyết bài 16 trang 78 Sách bài tập Toán 12 Chân trời sáng tạo. Chúc bạn học tập tốt!